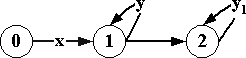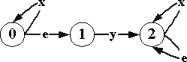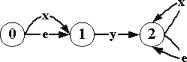Асинхронные автоматы:
классификация и тестирование

 

И.Б.Бурдонов, А.С.Косачев, В.В.Кулямин

Институт Системного Программирования РАН

e-mail: {igor@, kos@, kuliamin@ispras.ru}

 

Рассматриваются конечные автоматы, отличающиеся от классического автомата Мили тем, что переход осуществляется либо по приему стимула (входного символа), либо по выдаче реакции (выходного символа), причем в каждом состоянии выбор одного из допустимых переходов недетерминирован. Такими автоматами являются автоматы с отложенной реакцией (АОР), в которых переход по стимулу выполняется всегда, когда этот стимул имеется на входе автомата, и автоматы ввода-вывода (IOSM - Input/Output State Machines), в которых переход по выдаче реакции допустим независимо от наличия стимула, а не принятый в этом состоянии стимул может быть принят позже, в другом состоянии. Обобщением этих классов автоматов является асинхронный автомат, в котором допускаются также переходы по отсутствию стимула. Предлагается классификация асинхронных автоматов, основанная на реализуемой автоматом словарной функции и эквивалентности автоматов с совпадающей словарной функцией. Показывается, что класс всех асинхронных автоматов эквивалентен своему подклассу автоматов с отложенными реакциями, а словарные функции автоматов ввода-вывода образуют собственное подмножество всех автоматных словарных функций. С автоматом связывается также множество сериализаций (смешанных последовательностей воспринимаемых стимулов и выдаваемых реакций), и исследуется его связь со словарной функцией. Статья завершается обзором основных проблем тестирования соответствия, когда асинхронные автоматы используются как спецификационная модель программных и аппаратных систем.

 

Асинхронные автоматы: классификация и тестирование. 1

1. Введение. 2

2. Словарная функция. 6

2.1. Асинхронный автомат. 6

2.2. Финальная допустимость стимулов. 8

2.3. Автоматы без смешанных состояний. 10

2.4. Три класса автоматов и словарных функций. 16

2.4.1. Автоматы с отложенными реакциями (АОР) √ императивные автоматы без e-переходов═ 16

2.4.2. Автоматы ввода-вывода (IOSM) √ факультативные автоматы без e-переходов. 18

2.4.3. Автоматы без смешанных состояний и e-переходов (A0) 19

2.5. Общая картина взаимосвязей классов асинхронных автоматов с точки зрения словарной функции═ 21

3. Сериализация. 23

3.1. Сериализации и маршруты. 23

3.2. Три класса автоматов и z-множеств. 27

3.2.1. Класс автоматов A2, в которых z-раскраска совпадает с z-множеством (каждое нетерминальное срабатывание есть переход) 27

3.2.2. Класс автоматов A3, в которых все допустимые маршруты (сериализации) вполне-допустимы.. 27

3.2.3. Класс автоматов A4 с детерминированным z-множеством.. 30

3.3. Автоматные множества сериализаций, распознающие и отвергающие автоматы. 32

3.4. Квази-конечные сужения словарной функции и z-множества. 34

3.5. Предикат на конечных сериализациях. 36

3.5.1. Предикат z-множества. 38

3.5.2. Предикат словарной функции. 38

4. Проблемы тестирования соответствия. 41

4.1. Модель и реализация. Адаптивный алгоритм тестирования. 41

4.2. Проблема избыточности реализации. 43

4.3. Проблема избыточности модели. 44

4.4. Проблема недетерминизма. 44

4.5. Проблема бесконечности модельного домена. 45

4.6. Итерация входных слов. 45

4.7. Проблема бесконечных входных слов. 46

4.8. Проблема пустых стимулов. 48

4.8.1. Перехват операции receive. 48

4.8.2. Серийное тестирование без пауз и стационарное тестирование. 48

4.8.2. Автоматы с однородным поведением.. 49

4.8.4.═ Автоматы с однородной допустимостью.. 50

4.9. Проблема выходных слов. 52

4.9.1. Тайм-аут на ожидание очередной реакции. 52

4.9.2. Время ожидания репрезентативного выходного слова. 54

4.9.3. Автоматы с конечными выходными словами для квази-конечных входных слов. 55

4.10. Проблема постсостояния. 56

4.11. Проблема имплицитной спецификации модели и обход графа состояний. 57

4.13. Проблема медиаторов и многоуровневые спецификации. 58

5. Заключение. 59

Литература: 60

 

 

1. Введение

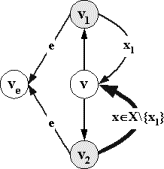
Понятие автомата с отложенными реакциями (АОР) было введено авторами настоящей статьи совместно с А.Хорошиловым для моделирования многопроцессной программной системы, интерфейс с которой основан на обмене сообщениями. В ответ на входное сообщение система может выдать несколько выходных сообщений, причем, если в процессе их выдачи поступает следующее входное сообщение, оно может изменить выходной поток. Целью моделирования являлось написание формальных спецификаций, на основе которых создавался тест для тестирования соответствия реализации спецификации. Поскольку внутреннее состояние тестируемой системы было недоступно, она рассматривалась как ╚черный ящик╩ и о ее поведении можно было судить только по ее реакциям (выходным сообщениям) на подаваемые стимулы (тестовые входные сообщения).

 

Автоматы с отложенными реакциями похожи на хорошо известные в литературе [1-6] автоматы ввода-вывода (IOSM √ Input/Output State Machines), называемые также взаимодействующими конечными автоматами (CFSM - Communicating Finite State Machines). В обоих автоматах переход из одного состояния в другой происходит либо как прием входного символа (стимула) √ принимающий переход, либо как выдача выходного символа (реакции) √ посылающий переход, либо как пустой переход, не сопровождающийся ни приемом стимула, ни выдачей реакции. Стимул допустим в некотором состоянии, если в этом состоянии определен принимающий переход по этому стимулу, в противном случае стимул недопустим в данном состоянии. Поскольку мы не требуем допустимости каждого стимула в каждом состоянии, рассматриваемые автоматы являются частично-определенными.═ Состояние автомата принимающее, если в нем определены только принимающие переходы, посылающее, если в нем определены только посылающие или пустые переходы, смешанное, если в нем определены как принимающие, так и посылающие или пустые переходы, и терминальное, если в нем никаких переходов не определено. Принимающие и смешанные состояния будем называть рецептивными (в этих состояниях возможен прием стимула).

 

Стимулы могут поступать на автомат только в рецептивном состоянии, но они не обязаны поступать в каждом его рецептивном состоянии. Переходы, допустимые в данном состоянии, определяются в зависимости от наличия или отсутствия стимула на входе автомата и, в случае наличия стимула, от самого этого стимула. Если оказывается, что таких допустимых переходов несколько, то выбирается один из них недетерминированным образом. В обоих автоматах, если состояние посылающее или рецептивное, но стимул отсутствует, то допустимыми являются посылающие и пустые переходы, определенные в этом состоянии. Различие между АОР и IOSM имеет место при определении допустимых переходов в случае наличия стимула в смешанном состоянии. Для АОР допустимы только принимающие переходы по этому стимулу и недопустимы как принимающие переходы по другим стимулам, так и посылающие и пустые переходы. Для IOSM также допустимы принимающие переходы по этому стимулу и недопустимы переходы по другим стимулам, однако посылающие и пустые переходы остаются допустимыми. При этом, если выполняется посылающий или пустой переход, то стимул остается на входе автомата в ожидании либо 1) выборки допустимого принимающего перехода по этому стимулу в другом рецептивном состоянии, либо 2) перехода в принимающее состояние, в котором не определен переход по данному стимулу. В случае 1) стимул выбирается автоматом и далее на его вход может поступить следующий стимул, а в случае 2) поведение автомата считается не определенным и это рассматривается как, так называемая, ошибка неспецифицированного ввода. Заметим, что для АОР такая ошибка фиксируется сразу же, как только на вход автомата поступает недопустимый в текущем состоянии стимул. Разумеется, возможно также выполнение автомата, при котором стимул никогда не будет выбран: если автомат перешел в терминальное состояние или бесконечно выполняются посылающие и пустые переходы (для АОР √ в посылающих состояниях). В терминальном состоянии автомат останавливается: состояние не меняется и прекращается как прием стимулов, так и выдача реакций. Хотя в терминальном состоянии все стимулы формально недопустимы, тем не менее ошибка неспецифицированного ввода не фиксируется, поскольку считается, что работа автомата закончена.

 

Классический автомат Мили, который на каждый допустимый стимул выдает ровно одну реакцию и ничего не делает при отсутствии стимулов, может рассматриваться как частный случай═ АОР и IOSM. Для этого достаточно каждый его переход, сопровождающийся приемом стимула и выдачей реакции, представить как последовательность из двух переходов: принимающего перехода по этому стимулу и посылающего перехода по этой реакции, между которыми добавляется═ промежуточное посылающее состояние (исходные нетерминальные состояния становятся принимающими, а смешанных состояний нет).

 

Тестирование соответствия основано на сравнении поведения двух автоматов: спецификационного, заданного явно, например, своим графом состояний, и реализационного, рассматриваемого как ╚черный ящик╩, о графе состояний которого и текущем состоянии мы не имеем информации, но можем судить о его поведении по тем реакциям, которые он выдает в ответ на поступающие к нему тестовые стимулы. Реализация считается соответствующей спецификации, если для любой последовательности стимулов (входного слова) автоматы выдают одинаковые последовательности реакций (выходные слова). Для недетерминированного спецификационного автомата более осмысленно говорить не о совпадении выходных слов, а о принадлежности любого выходного слова, выдаваемого реализацией, множеству выходных слов, разрешаемых спецификацией. Заметим, что при этом реализационный автомат может быть даже детерминированным (выходное слово однозначно определяется его начальным состоянием и входным словом). Иными словами, спецификация описывает не одну реализацию, а класс реализаций ей соответствующих (сводимых к ней).

 

С автоматом связана словарная функция, им реализуемая и определяемая как отображение═ входного слова, подаваемого на автомат, начиная с его начального состояния, во множество возможных выходных слов. Область ее определения включает только допустимые входные слова, то есть, такие, которые не могут при некотором возможном выполнении автомата вызвать ошибку неспецифицированного ввода. По существу, тестирование соответствия ставит своей задачей определение словарной функции реализационного автомата и сравнение ее со словарной функцией спецификационного автомата: область определения этих словарных функций предполагается одинаковой (по крайней мере, модельный домен вложен в реализационный), а тестирование проверяет, что для каждого допустимого входного слова значение на нем реализационной словарной функции вложено в значение спецификационной словарной функции.

 

Для классического автомата Мили такое определение словарной функции достаточно: все нетерминальные состояния рецептивны и подача на его вход допустимого входного слова длины n вызывает последовательность переходов через m£n рецептивных состояний, заканчивающуюся в m+1-ом терминальном или, если m=n, терминальном или рецептивном состоянии, и выдачу соответствующего выходного слова длины m. Однако, для АОР и IOSM, в которых посылающие и пустые переходы могут выполняться и при отсутствии стимулов,═ понятие словарной функции нуждается в уточнении. Для определения входного слова, кроме самой последовательности стимулов, нам следует рассматривать также ╚паузы╩ между соседними стимулами, которые естественно измерять в количестве рецептивных состояний, проходимых═ между приемом этих стимулов. Для моделирования прохода одного рецептивного состояния с отсутствием стимула на входе автомата удобно ввести понятие пустого стимула, расширив им алфавит стимулов. Если между двумя непустыми стимулами во входном слове располагается k пустых стимулов, то это означает, что автомат между приемами этих непустых стимулов пройдет k рецептивных состояний при отсутствии стимула на его входе. Пустой стимул считается допустимым в любом рецептивном состоянии.

 

После этого удобно ввести понятия входной и выходной очередей автомата. Во входной очереди располагается входное слово в расширенном алфавите стимулов, а в выходную очередь поступают выдаваемые автоматом реакции, формируя в ней выходное слово. Принимающий переход по (непустому) стимулу допустим только в том случае, когда в голове входной очереди располагается этот стимул. При выполнении такого перехода стимул удаляется из очереди. Напомним, что в этой ситуации в рецептивном состоянии АОР всегда выполняет принимающий переход, а IOSM может выполнить также посылающий или пустой переход, и тогда непустой стимул остается в голове входной очереди. Если же головной стимул очереди пустой, то он в автоматах обоих видов удаляется при посылающем или пустом переходе из рецептивного состояния. Посылающий переход помещает в выходную очередь соответствующую реакцию и, если это переход из посылающего состояния, не изменяет входной очереди и не зависит от её содержимого. После этого словарная функция определяется на множестве допустимых входных слов в расширенном алфавите стимулов таким образом, что если во входную очередь автомата поместить данное допустимое входное слово, то множество выходных слов, которые могут оказаться в выходной очереди, как раз и есть значение словарной функцией.

 

Теперь обратим внимание на то, что для того, чтобы поведение автомата было полностью определено, входное слово должно содержать в конце ╚достаточное╩ число пустых стимулов. Иначе, может сложиться ситуация, когда автомат переходит в рецептивное состояние, а входная очередь пуста, то есть, не содержит не только непустые, но и пустые стимулы, хотя последние как раз и предназначены для моделирования пустоты очереди. Более того, если автомат содержит цикл из пустых и посылающих переходов, проходящий хотя бы через одно рецептивное состояние,═ то таких концевых пустых стимулов должно быть бесконечное число. Это наталкивает на мысль рассматривать словарную функцию определенной не на конечных, а на бесконечных входных словах. Бесконечное слово, содержащее только конечное число непустых стимулов, является аналогом конечного слова и мы будем называть его квази-конечным словом.

 

Мы будем определять словарную функцию на всех допустимых бесконечных словах, а не только квази-конечных. Причина этого в том, что в отличии от классического автомата Мили, в АОР и IOSM такая словарная функция, вообще говоря, не восстанавливается однозначно по ее сужению на поддомене всех допустимых квази-конечных входных слов (см. ниже 3.5.2).

 

Теперь можно рассматривать естественное обобщение АОР и IOSM, заключающееся в том, что автомату разрешается выполнять принимающие переходы не только по непустому стимулу, но также и по пустому стимулу, то есть, поскольку пустой стимул моделирует отсутствие стимула, по отсутствию стимула на входе автомата. Такой переход будем называть e-переходом, а общий вид автомата с e-переходами - асинхронным автоматом, имея в виду, что выдача реакции происходит, вообще говоря, асинхронно с приемом стимула. (Наше понятие асинхронного автомата следует отличать от понятия асинхронно выполняющейся сети взаимодействующих автоматов.) Интерпретация поведения такого асинхронного автомата зависит от двух независимых факторов.

 

Во-первых, от вида того автомата, из которого этот асинхронный автомат произошел √ АОР или IOSM, а именно, является ли прием непустого стимула в рецептивном состоянии обязательным или не обязательным. В первом случае асинхронный автомат будем называть императивным, а во втором √ факультативным.

 

Во-вторых, поскольку удаление пустого стимула из головы входной очереди теперь может происходить при выборе либо, как раньше, посылающего или пустого перехода из рецептивного состояния, либо принимающего e-перехода, необходимо определиться с взаимным приоритетом этих двух видов переходов, если они определены в одном и том же смешанном состоянии. Приоритет может быть 1) у посылающих и пустых переходов; 2) у e-переходов; 3) они могут быть равноприоритетны.

 

Таким образом, всего может быть 8 базовых классов автоматов: императивный или факультативный, без e-переходов или с e-переходами и одним из трех указанных приоритетов e-переходов по отношению к посылающим и пустым переходам.

 

Статья состоит из четырех частей. 2-ая (после Введения) часть посвящена определению и сравнительному изучению асинхронных автоматов базовых классов. При этом, в первую очередь, обращается внимание на реализуемые ими словарные функции. С помощью преобразований автоматов, сохраняющих их словарную функцию, все автоматы приводятся к одному классу автоматов без смешанных состояний. На этой основе проводится классификация автоматов, в частности показывается эквивалентность класса всех асинхронных автоматов подклассу АОР √ императивных автоматов без e-переходов, и, напротив, показывается, что класс IOSM √ факультативных автоматов без e-переходов √ не способен моделировать класс всех асинхронных автоматов.

 

В 3-ей части изучаются реализуемые автоматами сериализации (смешанные последовательности стимулов и реакций) и маршруты (последовательности переходов). Вводятся понятия строгой моделируемости и строгой эквивалентности, основанные не на словарной функции, а на множестве реализуемых сериализаций, и показывается, что преобразования автоматов, использованные во 2-ой части, сохраняют не только словарную функцию, но и множество сериализаций. Устанавливается связь словарной функции и множества сериализаций автомата. Рассматриваются вопросы регулярности и существования отвергающих автоматов. Далее рассматриваются конечные сериализации, предикаты на множестве конечных сериализаций и индуцируемые такими предикатами семейства автоматов с соответствующими им словарными функциями.

 

4-ая часть посвящена проблемам тестирования соответствия для асинхронных автоматов. Проводится разделение на гипотезы √ предусловия тестирования, и тестируемые условия, проверяемые в процессе тестирования. Для каждой проблемы намечаются возможные пути ее решения.

═

2. Словарная функция

2.1. Асинхронный автомат

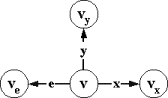
Асинхронным автоматом будем называть шестерку m=(V,v₀,X,e,Y,T), где:

╥        V - множество состояний;

╥        v₀ÎV √ начальное состояние;

╥        X - входной алфавит стимулов;

╥        eÏX - пустой стимул, X`=XÈ{e} √ расширенный алфавит стимулов;

╥        Y √выходной алфавит реакций;═ будем считать, что алфавиты стимулов и реакций не пересекаются X`ÇY= Æ;

╥        T = R`ÈSÈI - множество переходов, где:

o       R` Í V´X`´V - принимающие переходы,

o       S Í V´Y´V - посылающие переходы,

o       I Í V´V - пустые переходы.

 

Принимающие переходы можно разделить на два вида: R=R`ÇV´X´V √ принимающие переходы по непустым стимулам или x-переходы, и E=R`ÇV´{e}´V √ принимающие переходы по пустым стимулам или e-переходы.

 

Состояния можно разделить на терминальные, в которых не определены никакие переходы, посылающие, в которых определены только посылающие и пустые переходы, принимающие, в которых определены только принимающие переходы, и смешанные, в которых определены как принимающие, так и посылающие или пустые переходы. Принимающие и смешанные переходы будем называть рецептивными.

 

Стимул x допустим в состоянии v, если имеется хотя бы один принимающий переход (v,x,v`).

 

Автомат конечен, если конечны множества состояний V и переходов T. По умолчанию, мы будем рассматривать только конечные автоматы.

 

Такое определение автомата не полностью описывает его выполнение, поскольку дополнительно нужно указать, является ли автомат императивным или факультативным, разрешены ли в нем e-переходы и какой их приоритет по отношению к посылающим и пустым переходам. Введем обозначения:

╥        M=MiÈMf √ класс всех асинхронных автоматов,

╥        Mi=Mi0ÈMi1ÈMi2ÈMi3 √ императивные автоматы,

╥        Mf=Mf0ÈMf1ÈMf2ÈMf3 √факультативные автоматы,

╥        Mi0 (Mf0) √ императивные (факультативные) автоматы без e-переходов (E=Æ),

╥        Mi1 (Mf1) √ императивные (факультативные) автоматы с e-переходами и приоритетом посылающих и пустых переходов над e-переходами,

╥        Mi2 (Mf2) √ императивные (факультативные) автоматы с e-переходами и приоритетом e-переходов над посылающими и пустыми переходами,

╥        Mi3 (Mf3) √ императивные (факультативные) автоматы с e-переходами и равноприоритетностью посылающих и пустых переходов и e-переходов.

 

Будем считать, что с автоматом связаны две очереди: входная очередь, в которой располагается бесконечное входное слово в алфавите X`, и выходная очередь, в которую помещаются выдаваемые автоматом реакции, формируя выходное слово в алфавите Y. Срабатывание (однократное выполнение) автомата в состоянии v заключается в определении допустимых переходов, определенных в этом состоянии и, если такие есть, недетерминированном выборе одного из них и выполнении его. Если выбирается пустой переход (v,v`), автомат переходит в состояние v`, входная и выходная очереди не изменяются. Если выбирается принимающий переход (v,x,v`), то x √ головной стимул входной очереди и он удаляется из нее, автомат переходит в состояние v`, выходная очередь не изменяется. Если выбирается посылающий переход (v,y,v`), автомат переходит в состояние v`, а в конец выходной очереди помещается реакция y; если v √ смешанное состояние и головной стимул входной очереди пустой, то он удаляется из входной очереди, в противном случае входная очередь не изменяется. В срабатывание автомата входит также его действия в случае отсутствия допустимых переходов.

 

Множество допустимых переходов, а также действия автомата при отсутствии допустимых переходов, зависят в общем случае от состояния v, головного стимула x входной очереди и класса автомата:

╥        В терминальном состоянии v допустимых переходов нет. Автомат останавливается: состояние, входная и выходная очереди не изменяются.

╥        В посылающем состоянии v допустимые переходы - это все посылающие (v,y,v`) и пустые (v,v`) переходы.

╥        В принимающем состоянии v допустимые переходы √ это все принимающие переходы (v,x,v`). Если таких переходов нет, то выполнение автомата зависит от того, пустой или непустой головной стимул: если x¹e непустой (недопустимый) стимул, то поведение автомата не определено, это квалифицируется как ошибка неспецифицированного ввода; если же x=e пустой стимул, то автомат остается в состоянии v, а пустой стимул удаляется из входной очереди, выходная очередь не изменяется.

╥        В смешанном состоянии v:

o       Если x=e пустой стимул, то допустимые переходы:

╖         для автоматов Mi0,Mi1,Mf0,Mf1 - посылающие (v,y,v`) и пустые (v,v`) переходы;

╖         для автоматов Mf2,Mi2 - e-переходы (v,e,v`), а если их нет, то посылающие (v,y,v`) и пустые (v,v`) переходы;

╖         для автоматов Mf3,Mi3 - e-переходы (v,e,v`), если они есть, плюс посылающие (v,y,v`) и пустые (v,v`) переходы.

o       Если x¹e непустой допустимый стимул, то допустимые переходы:

╖         для императивных автоматов Mi - x-переходы (v,x,v`);

╖         для факультативных автоматов Mf - x-переходы (v,x,v`) плюс посылающие (v,y,v`) и пустые (v,v`) переходы.

o       Если x¹e непустой недопустимый стимул, то допустимые переходы:

╖         отсутствуют для императивных автоматов Mi - поведение автомата не определено, это квалифицируется как ошибка неспецифицированного ввода;

╖         для факультативных автоматов Mf - посылающие (v,y,v`) и пустые (v,v`) переходы.

 

Заметим, что класс автомата влияет на его срабатывание только в смешанных состояниях.

 

Выполнением автомата по бесконечному входному слову w будем называть последовательность однократных срабатываний, начинающуюся в начальном состоянии v₀, когда во входной очереди находится слово w. Подпоследовательность посылающих переходов определяет выходное слово u, появляющееся в выходной очереди при данном выполнении. Выполнение допустимо, если оно бесконечное или заканчивается в терминальном состоянии, и недопустимо, если оно заканчивается по ошибке неспецифицированного ввода. Поскольку автомат, вообще говоря, недетерминированный, одному входному слову может соответствовать множество возможных выполнений автомата. Входное слово допустимо, если все его возможные выполнения допустимы. Соответственно, выполнение по допустимому входному слову будем называть вполне-допустимым. Заметим, что вполне-допустимое выполнение допустимо, но обратное, вообще говоря, не верно. Словарная функция автомата W ставит в соответствие каждому допустимому входному слову w множество выходных слов u для всех возможных выполнений. Заметим, что входное слово не обязательно будет полностью выбрано из входной очереди при том или ином выполнении.

 

Допустимость входных слов и словарную функцию можно определить для любого состояния автомата, если его рассматривать как начальное состояние. В дальнейшем мы по умолчанию будем иметь в виде допустимость входных слов и словарную функцию для заданного начального состояния автомата v₀.

2.2. Финальная допустимость стимулов

Для факультативного автомата, в отличии от императивного, допустимость или недопустимость стимула x в смешанном состоянии v еще ничего не говорит о допустимости или недопустимости в этом состоянии входного слова w, начинающегося со стимула x, в частности, учитывая, что пустые стимулы допустимы во всех нерецептивных состояниях, слова xe^w. Введем понятие финальной допустимости стимула в факультативном автомате: непустой стимул финально допустим в рецептивном состоянии v, если он допустим в любом принимающем состоянии v`, в которое можно попасть из состояния v по цепочке посылающих и пустых переходов (цепочка будет нулевой длины, если v принимающее состояние). 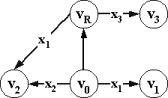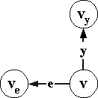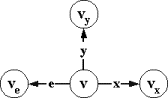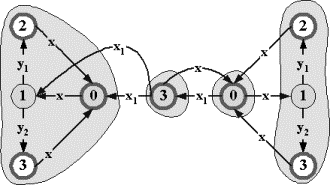Возможные сочетания допустимости и финальной допустимости стимулов приведены на рис.2.2.1.

 

Рис.2.2.1

 

Очевидно, для факультативного автомата входное слово допустимо тогда и только тогда, когда при любом выполнении автомата в проходимых рецептивных состояниях головные стимулы финально допустимы. Для принимающих состояний понятия допустимости и финальной допустимости стимулов совпадают. Однако, для смешанных состояний и допустимые и недопустимые стимулы могут быть как финально допустимы, так и финально недопустимы.

 

Обозначим через M`fÌMf, M`f1ÌMf1, M`f2ÌMf2, M`f3ÌMf3 подклассы факультативных автоматов, в которых допустимость и финальная допустимость стимулов совпадают.

 

Теорема о финальной допустимости стимулов: Каждый базовый класс факультативных автоматов моделируется своим подклассом автоматов, в которых совпадают допустимость и финальная допустимость стимулов, и, следовательно, эквивалентен ему: W[M`f]=W[Mf], W[M`f1]=W[Mf1], W[M`f2]=W[Mf2], W[M`f3]=W[Mf3].

 

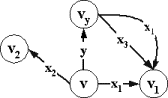
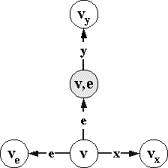
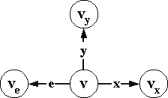
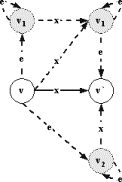
Док-во: Определим следующую процедуру преобразования факультативного автомата (рис.2.2.2):

╥        Добавим дополнительные состояния вида (v,x), где vÎV √ основное состояние, а xÎX - непустой стимул.

╥        Для каждого основного смешанного состояния v удалим все определенные в нем принимающие переходы (v,x,v`) по допустимым, но финально недопустимым стимулам x.

╥        Для каждого основного смешанного состояния v и недопустимого, но финально допустимого в нем стимула x, добавим принимающий переход, ведущий в дополнительное состояние (v,x,(v,x)).

╥        Если в основном рецептивном состоянии v стимул x финально допустим, то для каждого принимающего перехода (v,x,v`) добавим пустой переход из соответствующего дополнительного состояния ((v,x),v`).

╥        Для каждого посылающего (v,y,v`) и пустого (v,v`) перехода добавим, соответственно, посылающий ((v,x),y,(v`,x)) или пустой ((v,x),(v`,x)) переход из дополнительных состояний.

Рис.2.2.2

 

Теперь в каждом смешанном основном состоянии допустимы те и только те стимулы, которые финально допустимы. Дополнительные состояния - посылающие. Из этого правила есть одно важное исключение: основное смешанное состояние v может стать нерецептивным (посылающим), если окажется, что все непустые стимулы недопустимы в нем, и в нем не определены e-переходы. Нерецептивность состояния приводит к тому, что при выходе из него по посылающему или пустому переходу пустой головной стимул не удаляется из очереди. Иными словами, если в момент прихода в состояние v во входной очереди было слово ew, то после посылающего или пустого перехода, определенного в v, во входной очереди раньше оставалось слово w, а теперь, когда состояние стало нерецептивным, - то же самое слово ew. Здесь нужно рассмотреть два случая.

 

Случай 1. Если автомат не имеет e-переходов (класс Mf0), то финальная недопустимость стимула x в состоянии v означает существование выполнения, начинающегося в v, содержащего только посылающие и пустые переходы и заканчивающегося в принимающем состоянии v`, в которой стимул x недопустим. Поскольку в v` не определены e-переходы, сначала будут удалены из очереди все пустые стимулы, а потом выбран непустой стимул и, если это x, то фиксируется ошибка неспецифицированного ввода. Следовательно из финальной недопустимости стимула x в смешанном состоянии v следует финальная недопустимость в нем любого слова eⁿx. Тем самым, если в состоянии v недопустимы все непустые стимулы, то в этом состоянии допустимо единственное бесконечное слово e^w (которое всегда допустимо). Поскольку для ew=e^w, очевидно, w=e^w, имеем ew=w и, следовательно, словарная функция не меняется.

 

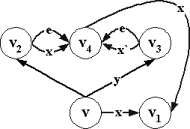
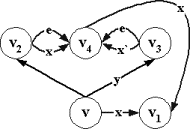
Случай 2. Если автомат может иметь e-переходы (классы Mf1, Mf2, Mf3), то, вообще говоря, из финальной недопустимости стимула x в состоянии v не следует финальная недопустимость в нем слова ex, то есть, финальная недопустимость стимула x в конце v` какого-нибудь e-перехода (v,e,v`). Простое удаление принимающих переходов, определенных в v, может изменить словарную функцию. Пример на рис.2.2.3.

 

Рис.2.2.3

 

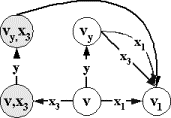
Поэтому для таких автоматов, кроме удаления принимающих переходов (v,x,v₁) из состояния v, мы дополнительно преобразуем хотя бы один пустой (v,v₂) или посылающий (v,y,v₃) переход из v, в два смежных перехода, первый из которых - e-переход (v,e,v₂`), ведущий в дополнительное состояние v<sub>2</sub>`, а второй пустой (v₂`,v`) переход, или, соответственно, e-переход (v,e,v₃`) и посылающий (v<sub>3</sub>`,y,v`) переход. Состояние v остается рецептивным, а движение по паре новых смежных переходов эквивалентно (по изменению состояния и содержимого очередей) движению по одному старому переходу. 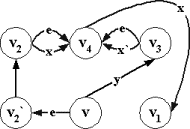Поэтому и в этом случае словарная функция не меняется. См. Рис.2.2.4.

 

Рис.2.2.4

 

Теорема о финальной допустимости стимулов доказана.

 

В дальнейшем мы вместо базовых классов Mf, Mf1, Mf2, Mf3 будем рассматривать эквивалентные им подклассы M`f, M`f1, M`f2, M`f3, которые также будем называть базовыми классами факультативных автоматов там, где это не приведет к недоразумениям.

2.3. Автоматы без смешанных состояний

Обозначим через A класс автоматов без смешанных состояний с e-переходами. Отсутствие смешанных состояний и возможное наличие e-переходов делает автомат этого класса одновременно элементом любого из базовых классов с разрешенными e-переходами, которые отличаются друг от друга поведением только в смешанных состояниях, то есть, A = Mi3ÇMi2ÇMi1ÇM`f3ÇM`f2ÇM`f1. Тем самым, класс A моделируется каждым из базовых классов: W[A]ÍW[Mi3], W[A]ÍW[Mi2], W[A]ÍW[Mi1], W[A]ÍW[M`f3], W[A]ÍW[M`f2], W[A]ÍW[M`f1].

 

Теорема об автомате без смешанных состояний: Класс M всех асинхронных автоматов моделируется своим подклассом A автоматов без смешанных состояний и, следовательно, эквивалентен ему.

 

Из этой теоремы следует эквивалентность W[A]=W[Mi3]=W[Mi2]=W[Mi1]=W[M`f3]=W[M`f2]=W[M`f1] и вложенности W[Mi0]ÍW[A] и W[Mf0]ÍW[A].

 

Док-во: Для доказательства достаточно рассмотреть возможные срабатывания автоматов разных классов в смешанных состояниях. Можно выделить 11 случаев, изображенных на таб.2.3.1. Здесь переход, помеченный ⌠x■, означает принимающий переход по непустому стимулу x; переход, помеченный ⌠e■, означает e-переход; переход, помеченный ⌠y■, означает переход посылающий реакцию y или пустой переход. Записи x:(...) и e:(...) означают здесь допустимость перехода (...) когда головной стимул входной очереди равен, соответственно, непустому стимулу x или пустому стимулу e.

Таб.2.3.1

 

1. Смешанное состояние без e-переходов.

1.1. Императивный автомат (рис.2.3.1).

Рис.2.3.1

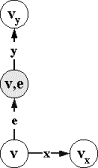
Для каждого состояния v типа 1 добавляется дополнительное состояние (v,e). Посылающий (v,y,v`<sub>y</sub>) или пустой (v,v`_y) переход из v заменяется на e-переход, ведущую в дополнительное состояние (e,v,(v,e)) и, соответственно, посылающий ((v,e),y,v_y) или пустой ((v,e),v_y) переход из этого дополнительного состояния.

 

1.2. Факультативный автомат (рис.2.3.2).

Рис.2.3.2

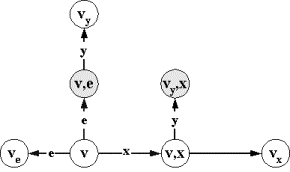
Аналогично случаю 1.1, для каждого состояния v типа 1 добавляется дополнительное состояние (v,e); посылающий (v,y,v`<sub>y</sub>) или пустой (v,v`_y) переход из v заменяется на e-переход в дополнительное состояние (e,v,(v,e)) и, соответственно, посылающий ((v,e),y,v_y) или пустой ((v,e),v_y) переход из этого дополнительного состояния. Затем в моделирующий автомат добавляются дополнительные состояния вида (v,x) для состояний vÎV и непустых стимулов xÎX. Для каждого основного смешанного состояния vÎV рассматриваемого типа и допустимого в нем непустого стимула x добавляется принимающий переход (v,x,(v,x)). В каждом дополнительном состоянии (v,x) определяются посылающие ((v,x),y,(v`,x)) и пустые ((v,x),(v`,x)) переходы тогда и только тогда, когда в моделируемом автомате есть переходы, соответственно, (v,y,v`) и (v,v`). В каждом дополнительном состоянии (v,x) определяется пустой переход ((v,x),v`) тогда и только тогда, когда в моделируемом автомате есть переход (v,x,v`).

 

 

 

 

 

 

 

 

 

 

2. Смешанное состояние, в котором все принимающие переходы - e-переходы.

2.1. Равный приоритет e-переходов и посылающих и пустых переходов (рис.2.3.3).

Рис.2.3.3

Аналогично случаю 1.1, для каждого состояния v типа 2 добавляется дополнительное состояние (v,e); посылающий (v,y,v`<sub>y</sub>) или пустой (v,v`_y) переход из v заменяется на e-переход в дополнительное состояние (e,v,(v,e)) и, соответственно, посылающий ((v,e),y,v_y) или пустой ((v,e),v_y) переход из этого дополнительного состояния.

 

2.2. Приоритет e-переходов (рис.2.3.4).

Рис.2.3.4

Приоритет e-переходов приводит к тому, что в состоянии типа 2 вообще никогда не будут выполняться посылающие и пустые переходы, поэтому их можно удалить.

 

2.3. Приоритет посылающих и пустых переходов (рис.2.3.5).

Рис.2.3.5

Приоритет посылающих и пустых переходов приводит к тому, что в состоянии типа 2 вообще никогда не будут выполняться e-переходы. Однако, если такие переходы просто удалить, то состояние перестанет быть рецептивным. Поэтому, как и в случае 1.1, для каждого состояния v типа 2 добавляется дополнительное состояние (v,e); посылающий (v,y,v`<sub>y</sub>) или пустой (v,v`_y) переход из v заменяется на e-переход в дополнительное состояние (e,v,(v,e)) и, соответственно, посылающий ((v,e),y,v_y) или пустой ((v,e),v_y) переход из этого дополнительного состояния.

 

3. Смешанное состояние общего вида.

3.1. Императивный автомат.

3.1.1. Равный приоритет e-переходов и посылающих и пустых переходов (рис.2.3.6).

Рис.2.3.6

Аналогично случаю 2.1, для каждого состояния v типа 3 добавляется дополнительное состояние (v,e); посылающий (v,y,v`<sub>y</sub>) или пустой (v,v`_y) переход из v заменяется на e-переход в дополнительное состояние (e,v,(v,e)) и, соответственно, посылающий ((v,e),y,v_y) или пустой ((v,e),v_y) переход из этого дополнительного состояния.

 

3.1.2. Приоритет e-переходов (рис.2.3.7).

Рис.2.3.7

Аналогично случаю 2.2, приоритет e-переходов приводит к тому, что в состоянии типа 3 вообще никогда не будут выполняться посылающие и пустые переходы, ═поэтому их можно удалить.

 

3.1.3. Приоритет посылающих и пустых переходов (рис.2.3.8).

Рис.2.3.8

Приоритет посылающих и пустых переходов приводит к тому, что в состоянии типа 3 вообще никогда не будут выполняться e-переходы. Удаляя e-переходы, получаем случай 1.1 и применяем соответствующее преобразование.

 

3.2. Факультативный автомат.

3.2.1. Равный приоритет e-переходов и посылающих и пустых переходов (рис.2.3.9).

Рис.2.3.9

Аналогично случаю 1.2, для каждого состояния v типа 3 добавляется дополнительное состояние (v,e); посылающий (v,y,v`<sub>y</sub>) или пустой (v,v`_y) переход из v заменяется на e-переход в дополнительное состояние (e,v,(v,e)) и, соответственно, посылающий ((v,e),y,v_y) или пустой ((v,e),v_y) переход из этого дополнительного состояния. Затем в моделирующий автомат добавляются дополнительные состояния вида (v,x) для состояний vÎV и непустых стимулов xÎX. Для каждого основного состояния v типа 3 и допустимого в нем непустого стимула x добавляется принимающий переход (v,x,(v,x)). В каждом дополнительном состоянии (v,x) определяются посылающие ((v,x),y,(v`,x)) и пустые ((v,x),(v`,x)) переходы тогда и только тогда, когда в моделируемом автомате есть переходы, соответственно, (v,y,v`) и (v,v`), кроме того, определяется пустой переход ((v,x),v`) тогда и только тогда, когда в моделируемом автомате есть переход (v,x,v`).

 

3.2.2. Приоритет e-переходов (рис.2.3.10).

Рис.2.3.10

Приоритет e-переходов приводит к тому, что в состоянии типа 3 при пустом головном стимуле не будут выполняться посылающие и пустые переходы; эти переходы могут выполняться только при непустом и допустимом головном стимуле. Поэтому делаем аналогично случаю 3.2.1, но только посылающий или пустой переход из основного состояния типа 3 не заменяем на e-переход в дополнительное состояние, и, соответственно, посылающий или пустой переход из этого дополнительного состояния, а просто удаляем. В моделирующий автомат добавляются дополнительные состояния вида (v,x) для состояний vÎV и непустых стимулов xÎX. Для каждого основного состояния v типа 3 и допустимого в нем непустого стимула x добавляется принимающий переход (v,x,(v,x)). В каждом дополнительном состоянии (v,x) определяются посылающие ((v,x),y,(v`,x)) и пустые ((v,x),(v`,x)) переходы тогда и только тогда, когда в моделируемом автомате есть переходы, соответственно, (v,y,v`) и (v,v`), кроме того, определяется пустой переход ((v,x),v`) тогда и только тогда, когда в моделируемом автомате есть переход (v,x,v`). Посылающие и пустые переходы из основных состояний типа 3 удаляются.

 

 

 

3.2.3. Приоритет посылающих и пустых переходов (рис.2.3.11).

Рис.2.3.11

Приоритет посылающих и пустых переходов приводит к тому, что в состоянии типа 3 при пустом головном стимуле не будут выполняться e-переходы; тем более они не будут выполняться при непустом головном стимуле. Поэтому делаем аналогично случаю 3.2.1, но только e-переходы из основных состояний типа 3 удаляем. В моделирующий автомат добавляются дополнительные состояний вида (v,x) для состояний vÎV и непустых стимулов xÎX. Для каждого основного состояния v типа 3 и допустимого в нем непустого стимула x добавляется принимающий переход (v,x,(v,x)). В каждом дополнительном состоянии (v,x) определяются посылающие ((v,x),y,(v`,x)) и пустые ((v,x),(v`,x)) переходы тогда и только тогда, когда в моделируемом автомате есть переходы, соответственно, (v,y,v`) и (v,v`), кроме того, определяется пустой переход ((v,x),v`) тогда и только тогда, когда в моделируемом автомате есть переход (v,x,v`). e-переходы из основных состояний типа 3, удаляются.

 

Теорема об автомате без смешанных состояний доказана.

2.4. Три класса автоматов и словарных функций

В этом разделе мы рассмотрим три класса автоматов: 1) класс Mi0=АОР императивных автоматов без e-переходов (автоматы с отложенными реакциями), 2) класс Mf0=IOSM факультативных автоматов без e-переходов (автоматы ввода-вывода), 3) пересечение этих классов - класс A0 автоматов без смешанных состояний и e-переходов. Мы покажем, что класс АОР моделирует класс A и, тем самым, эквивалентен классу всех асинхронных автоматов W[АОР]=W[M], класс IOSM этим свойством не обладает, то есть, W[IOSM]ÌW[M], а класс A0 не моделирует класс IOSM, W[A0]ÌW[IOSM], и, тем более, класс АОР, то есть, является самым узким классом в смысле словарной функции.═

2.4.1. Автоматы с отложенными реакциями (АОР) √ императивные автоматы без e-переходов

Сначала мы рассмотрим специальный подкласс A1ÌA автоматов без смешанных состояний и без таких принимающих состояний, в которых определены только e-переходы (такие состояния будем называть e-состояниями), то есть, в каждом принимающем состоянии определен хотя бы один принимающий переход по непустому допустимому стимулу.

 

Теорема о e-состояниях: Класс A моделируется своим подклассом A1 и, тем самым, они эквивалентны W[A]=W[A1].

 

Док-во: Для доказательства достаточно рассмотреть моделирование поведения автомата класса A в e-состоянии (рис.2.4.1), поскольку в остальных состояниях автоматы классов A и A1 ведут себя одинаково.

Рис.2.4.1

Для каждого e-состояния v добавляем два дополнительных состояния v₁ и v₂, и в состоянии v определяем два пустых перехода в v₁ и v₂. В состоянии v₁ определяем принимающий переход по любому непустому стимулу x, а в состоянии v₂ - множество принимающих переходов по всем остальным непустым стимулам. Очевидно, что в состоянии v все непустые стимулы финально недопустимы. После этого каждый e-переход (v,e,v_e) заменяем на два e-перехода из состояний v₁ и v₂, соответственно, (v₁,e,v_e) и (v₂,e,v_e).

 

В этом доказательстве мы неявно использовали тот факт, что алфавит стимулов состоит хотя бы из двух непустых стимулов, то есть, x₁ÎX и X\{x₁}¹Æ. Если это не так, то мы всегда можем добавить в алфавит стимулов еще два непустых стимула, один из которых будем использовать только для принимающих переходов из v₁, а другой вместе с остальными стимулами из X - для принимающих переходов из v₂. Понятно, что эти дополнительные стимулы не будут входить в допустимые входные слова, поэтому словарная функция не изменится.

 

Теорема о e-состояниях доказана.

 

Теорема об автомате с отложенными реакциями: Класс M всех асинхронных автоматов моделируется своим подклассом автоматов с отложенными реакциями АОР=Mi0 (императивные автоматы без e-переходов) и, следовательно, эквивалентен ему.

 

Док-во: Класс Mi0, как подкласс класса M всех асинхронных автоматов, им моделируется. Поскольку класс M всех асинхронных автоматов эквивалентен классу A, а класс A эквивалентен своему подклассу A1, нам достаточно показать, что класс A1 моделируется классом Mi0. Для моделирования автомата класса A1 автоматом класса Mi0 достаточно рассмотреть поведение автомата в принимающих состояниях, в которых определены прием как пустого стимула, так и непустых допустимых стимулов, поскольку в автоматах класса A1 нет смешанных состояний и нет e-состояний, а в принимающих состояниях без e-переходов также как═ в терминальных и посылающих состояниях все автоматы ведут себя одинаково. Моделирование поведения в таком состоянии тривиально: e-переходы заменяем пустыми переходами (рис.2.4.2).

Рис.2.4.2

Теорема об автомате с отложенными реакциями доказана.

 

Итак, мы показали, что W[Mi0]=W[A]=W[A1] и, тем самым, доказана эквивалентность всех базовых классов, кроме Mf0: W[M]=W[A]=W[A1]=W[Mi0]=W[Mi3]=W[Mi2]=W[Mi1]=W[M`f3]=W[M`f2]=W[M`f1].

2.4.2. Автоматы ввода-вывода (IOSM) √ факультативные автоматы без e-переходов

Теорема об автомате ввода-вывода (IOSM): Класс M всех асинхронных автоматов не моделируется своим подклассом автоматов ввода-вывода IOSM=Mf0 (факультативные автоматы без e-переходов).

 

Док-во: Поскольку класс Mf0 моделируется своим подклассом M`f0, а класс M всех асинхронных автоматов моделируется подклассом A, нам достаточно показать, что существует автомат aÏA, который не моделируется классом M`f0, то есть, W[a]ÏW[M`f0].

 

Напомним, что автомат класса M`f0 - это факультативный автомат без e-переходов, в котором совпадают допустимость и финальная допустимость стимулов. Такие автоматы обладают следующими двумя свойствами, которыми некоторые асинхронные автоматы класса A не обладают.

 

Свойство 1: Если словарная функция автомата класса M`f0 определена на входном слове uexw, где u - конечное слово, e - пустой стимул, x - некоторый стимул (быть может, пустой), w - бесконечное слово, то она должна быть определена также на входном слове uxe^w.

 

Действительно, поскольку входные слова uexw и uxe^w имеют общий начальный отрезок u, и слово uexw допустимо, ошибка неспецифицированного ввода может проявиться для слова uxe^w только после выборки слова u из входной очереди при приеме стимула x в принимающем состоянии v (последующие стимулы пустые и, тем самым, всегда допустимые). Значит стимул x недопустим в состоянии v. Но тогда для слова uexw автомат после выборки слова u также может оказаться в принимающем состоянии v и примет пустой стимул e. Поскольку v √ принимающее состояние и e-переходов нет, выборка пустого стимула не меняет состояние и автомат в том же состоянии v выберет недопустимый стимул x, то есть, будет зафиксирована ошибка неспецифицированного ввода и окажется, что слово uexw недопустимо. Мы пришли к противоречию и, значит, входное слово uxe^w должно быть допустимо.

 

Заметим, что требование наличия после непустого стимула x в слове uxe^w только пустых стимулов существенно, поскольку может оказаться, что для любого допустимого входного слова вида uexw любое входное слово вида uxw`, допустимо только тогда, когда w`=e^w. Пример приведен на рис. 2.4.3. При X = {x,x`} единственное допустимое слово вида xw` - это слово xe^w, а для всех допустимых входных слов вида uexw, u - должно быть пусто.

Рис.2.4.3

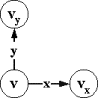
Теперь нам достаточно привести пример автомата класса A, словарная функция которого не обладала бы этим первым свойством (рис. 2.4.4). Словарная функция автомата определена на и только на словах вида ew, начинающихся с пустого стимула, и отображает каждое такое входное слово в пустое выходное слово. Для любого непустого стимула x эта функция определена на любом слове вида exw, но не определена на слове xe^w.

Рис.2.4.4

 

Свойство 2: Если словарная функция W автомата класса M`f0 определена на слове w, то она определена также на любом слове w`, полученное из w добавлением в произвольные места произвольного числа пустых стимулов, и W(w`)ÍW(w).

 

Действительно, если по конечному слову u автомат может попасть в принимающее состояние v, то, поскольку в принимающем состоянии не определены e-переходы, автомат в состоянии v не сможет различить остатки входных слов, находящиеся во входной очереди в этот момент времени, отличающиеся только количеством пустых стимулов в начале. Все эти пустые стимулы будут "глотаться" принимающим состоянием. Поэтому любое возможное продолжение выполнения автомата для допустимого слова uw дает ту же последовательность переходов (а значит, и реакций), что и для слова uew, и наоборот. Если по конечному слову u автомат может попасть в смешанное состояние v, то, поскольку в смешанном состоянии автомат может сработать по посылающему или пустому переходу независимо от головного стимула, пустой головной стимул в этом случае выбирается из очереди, а непустой остается, любое продолжение выполнения автомата для бесконечного слова uew дает такую последовательность переходов (а значит, и реакций), которая возможна также для продолжения выполнения в случае слова uw, хотя обратное, вообще говоря, неверно. Тем самым оказывается, что любое выполнение для слова uew дает последовательность переходов (а значит, и реакций), которая возможна также для слова uw, то есть, W(uew)ÍW(uw). Отсюда непосредственно следует свойство 2.

 

Теперь нам достаточно привести пример автомата класса A, словарная функция которого не обладала бы этим вторым свойством (рис.2.4.5). Здесь для═ X={x,x`} слово xx`e^w допустимо, а слово xex`e^w недопустимо.

Рис.2.4.5

 

Теорема об автомате ввода-вывода (IOSM) доказана.

 

Рассмотренные нами два свойства словарной функции автоматов ввода-вывода (IOSM)═ являются необходимыми. Можно сформулировать следующую нерешенную задачу: найти свойства словарной функции, необходимые и достаточные для того, чтобы она была словарной функцией автомата ввода-вывода (IOSM).

2.4.3. Автоматы без смешанных состояний и e-переходов (A0)

Специальный интерес представляет класс A0 автоматов без смешанных состояний и e-переходов, вложенный, очевидно, во все остальные рассматривавшиеся выше классы автоматов.

 

Теорема об автомате без смешанных состояний и e-переходов: Класс M`f0 не моделируется классом A0.

 

Док-во: Автоматы класса A0 обладают тремя особыми свойствами, которыми не обладают некоторые автоматы надкласса M`f0.

═

Свойство 1: Если словарная функция W автомата класса A0 определена на слове w, то она определена также на любом слове w`, полученном из w вставкой или удалением конечного числа пустых стимулов, и принимает на нем то же значение W(w`)=W(w).

 

Это непосредственно следует из того, что каждое рецептивное состояние является принимающим состоянием без e-переходов, поэтому такое состояние "глотает" все пустые стимулы. Примером автомата класса M`f0, не моделируемого классом A0 из-за нарушения свойства 1, может служить автомат на рис.2.4.3. Для X = {x,x`} входное слово exx`e<sup>w</sup> допустимо, а входное слово xx`e^w недопустимо. Заметим, что здесь мы использовали только часть свойства 1 класса A0 - выделенную курсивом. 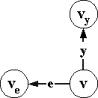Если использовать это свойство полностью, то можно привести более простой пример автомата класса M`f0, не моделируемого классом A0 (рис.2.4.6). Для этого автомата допустимы как входное слово xw, так и входное слово exw, где w - произвольное бесконечное слово. Однако, для слова exw определено одно выходное слово - (y), а для слова xw - два выходных слова: пустое () и (y).

Рис.2.4.6

 

Для того, чтобы определить второе свойство автоматов класса A0, введем следующие обозначения:

╥        c£c`, где c и c` - два слова (конечных или бесконечных) в одном алфавите, означает, чтоили c конечно и является начальным отрезком c`, или они совпадают.

╥        C£C`, где C и C` - два множества слов (конечных или бесконечных) в одном алфавите, означает, что "cÎC $c`ÎC` c£c` и "c`ÎC` $cÎC c£c`. Будем писать C<C`, если C£C` и С¹С`; очевидно, что в случае строгого неравенства C содержит хотя бы одно конечное слово.

 

Свойство 2: Если словарная функция W автомата класса A0 определена на слове ue^w, где u - конечное слово, то для любого допустимого слова uw имеет место W(ue^w)£W(uw).

 

Действительно, после выборки автоматом из входной очереди входного слова u автомат либо через конечное число посылающих и пустых переходов попадает в 1) принимающее или 2) терминальное состояние v и в выходной очереди оказывается конечное слово c, либо 3) выполняет бесконечную последовательность посылающих и пустых переходов. В случаях 2 и 3, очевидно, прекращается выборка стимулов из входной очереди и поэтому получившееся выходное слово принадлежит как W(ue^w), так и W(uw). В случае 1 автомат остается в принимающем состоянии v и более ничего не помещает в выходную очередь, то есть, выходным словом останется конечное слово c. В то же время для любого допустимого продолжения слова u, то есть, для слова uw автомат выполняет принимающий переход по первому непустому стимулу в слове w, то есть, выходное слово будет некоторым, быть может, пустым, продолжением c`³c.

 

Примером автомата класса M`f0, не моделируемого классом A0 из-за нарушения свойства 2, может служить тот же автомат на рис.2.4.6. Для этого автомата при xÎX допустимы как входное слово xw, где w - произвольное бесконечное слово, так и входное слово e^w. При этом W(e^w)={(y)}, а W(xw)={(),(y)}, и, очевидно, W(xw)<W(e^w).

 

Свойство 3: Если словарная функция W автомата класса A0 определена на слове ue^w, где u - конечное слово, и существует недопустимое слово uw, где w - бесконечное слово, содержащее непустые стимулы, то в множестве выходных слов W(ue^w) имеется хотя бы одно конечное слово.

 

Действительно, если существует недопустимое слово uw, то, значит, после выборки из входной очереди слова u, автомат может за конечное число посылающих и пустых переходов перейти в принимающее состояние v, в котором первый непустой стимул слова w недопустим. В этот момент в выходной очереди окажется конечное выходное слово c. Очевидно, что для входного слова ue^w дальше будут выбираться только пустые стимулы и автомат класса A0 будет оставаться в состоянии v, не изменяя выходную очередь. Это значит, что при таком выполнении для входного слова ue^w будет получено конечное выходное слово c, то есть, cÎW(ue^w).

 

Заметим, что если для некоторого допустимого слова uw имеет место W(ue^w)<W(uw), то из определения отношения "<" следует, что W(ue^w) содержит хотя бы одно конечное слово. Поэтому необходимым и достаточным условием отсутствия в W(ue^w)═ конечных слов является отсутствие недопустимых слов вида uw и для всех допустимых слов вида uw равенство (с учетом свойства 2) W(ue^w)=W(uw).

 

Пример автомата класса M`f0, не моделируемого классом A0 из-за нарушения свойства 3, приведен на рис.2.4.7. В этом автомате для X={x,x`} W(e^w)={y^w} и в тоже время существует недопустимое слово xx`w, где w - любое бесконечное слово.

 

Рис.2.4.7

 

Теорема об автомате без смешанных состояний и e-переходов доказана.

 

Рассмотренные нами три свойства словарной функции автоматов без смешанных состояний и e-переходов являются необходимыми. Можно сформулировать следующую нерешенную задачу: найти свойства словарной функции, необходимые и достаточные для того, чтобы она была словарной функцией автомата класса A0.

2.5. Общая картина взаимосвязей классов асинхронных автоматов с точки зрения словарной функции

Если рассматривать автоматы, в которых e-переходы определены только в принимающих состояниях (не определены в смешанных состояниях), то, очевидно, мы получим следующие классы автоматов Bi=Mi1ÇMi2=Mi1ÇMi3=Mi2ÇMi3, Bf=Mf1ÇMf2=Mf1ÇMf3=Mf2ÇMf3,

B`f=M`f1ÇM`f2=M`f1ÇM`f3=M`f2ÇM`f3.

 

Теперь определим разбиение класса всех асинхронных автоматов на непересекающиеся области (таб.2.5.1)

 

 

 

Таб.2.5.1

 

Теперь можно представить классы автоматов как объединения областей (таб.2.5.2).

Таб.2.5.2

 

 

 

 

В разделах 2.2-2.4 было показано следующее:

╥         Каждый базовый класс факультативных автоматов Mfn (n=0,1,2,3) моделируется своим подклассом M`fn, в котором допустимость и финальная допустимость стимулов совпадают, и, следовательно эквивалентен ему.

╥         Класс A моделирует базовые классы Min и M`fn, где n=0,1,2,3. Учитывая вложенность классов, получаем эквивалентность класса A и классов Min и M`fn, где n=1,2,3.

╥         Класс A моделируется своим подклассом A1 и, тем самым, ему эквивалентен.

╥         Эквивалентность класса A1 и класса Mi0.

╥         Немоделируемость класса A классом M`f0.

╥         Немоделируемость класса M`f0 классом A0.

Тем самым, учитывая вложенность классов, имеем три группы классов M0, M1, M таких, что W(M0)ÌW(M1)ÌW(M0), и все классы одной группы эквивалентны:

╥         W(M0) = W(A0)

╥         W(M1) = W(M`f0) = W(Mf0)

╥         W(M) = W(A1) = W(A) = W(Mi0) = W(Bi) = W(Mi1) = W(Mi2) = W(Mi3) = W(B`f) = W(M`f1) = W(M`f2) = W(M`f3) = W(Bf) = W(Mf1) = W(Mf2) = W(Mf3)

На рис.2.5.1 изображены эти три группы классов; стрелки показывают частичный порядок по отношению вложенности.

 

 

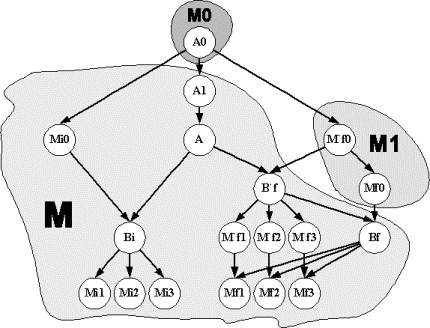
Рис.2.5.1

 

3. Сериализация

3.1. Сериализации и маршруты.

Зависимость между тестовыми воздействиями и реакциями тестируемого автомата, которую можно определить за конечное число тестовых экспериментов, может оказаться недостаточной для проверки соответствия реализации модели даже при допущении ряда довольно сильных предположений (гипотез) о тестируемом автомате. Здесь на помощь может придти возможность (когда она существует) определить в процессе тестирования не только последовательность реакций, выдаваемых автоматом в ответ на данную последовательность стимулов, но и относительное расположение во времени стимулов и реакций. Смешанную последовательность воспринимаемых автоматом стимулов и выдаваемых им реакций мы будем называть сериализацией. Начиная с этого раздела, мы будем исследовать сериализации, реализуемые автоматом, и их связь со словарной функцией. Разные автоматы, реализующие одну и ту же словарную функцию, отличаются как раз сериализациями. Преобразования автоматов из разделов 2.2-2.4 сохраняют не только словарную функцию, но и сериализации выполнений для допустимых входных слов.

 

Заметим, что подпоследовательность реакций сериализации совпадает с выходным словом. В то же время, поскольку автомат с некоторого момента может прекратить выборку стимулов из входной очереди, подпоследовательность стимулов сериализации может не совпадать со входным словом, а являться его начальным отрезком. Мы покажем, что это явление носит принципиальный характер, то есть, для некоторых словарных функций любой реализующий их конечный автомат выбирает из входной очереди лишь конечное число стимулов для некоторых допустимых входных слов. Выполнению автомата соответствует также маршрут - последовательность смежных переходов и, тем самым, раскраска маршрута как последовательность стимулов и реакций непустых переходов. Мы покажем связь маршрутов и их раскрасок с сериализациями.

 

Сериализацией будем называть слово (конечное или бесконечное)═ в объединенном алфавите стимулов (включая пустой) и реакций Z=X`ÈY. Через xz и yz обозначим, соответственно, x-подслово и y-подслово z, то есть, подпоследовательность z, состоящую из, соответственно стимулов и реакций. Мы будем также говорить, что z является сериализацией пары (zx,zy). Для множества сериализаций S обозначим xS={xz|zÎS} и yS={yz|zÎS}. На множестве всех сериализаций (как и вообще на множестве слов в любом алфавите) имеется естественный частичный порядок: z£z` означает, что сериализация z является начальным отрезком (тогда она конечна) или совпадает с сериализацией z`.

 

Сериализация z, соответствующая выполнению автомата любого класса, строится в процессе выполнения следующим образом. Реакция y помещается в z одновременно с выдачей этой реакции в выходную очередь, то есть, когда автомат совершает посылающий переход (v,y,v`). Стимул x`ÎX` помещается в z тогда, когда автомат впервые его ╚распознает╩, то есть, ╚читает╩ в рецептивном состоянии v для того, чтобы определить свое дальнейшее поведение в зависимости от этого стимула. Если дальнейшее поведение заключается в совершении принимающего перехода (v,x`,v`), то стимул удаляется из очереди и мы присоединим его к z: z^(x`). Однако, дальнейшее поведение не обязательно включает принимающий переход (v,x`,v`) по стимулу и/или удаление стимула из входной очереди. Для пустого стимула x`=e автоматы некоторых классов═ в смешанном состоянии v могут совершить посылающий (v,y,v`) или пустой (v,v`) переход (если в этом состоянии нет e-переходов или они имеют равный или меньший приоритет, чем посылающие и пустые переходы) и, тем самым, в z помещается два символа z^(ey) или один символ z^(e). Для принимающего состояния v без e-переходов при срабатывании автомата по пустому головному стимулу никакого перехода не совершается, состояние не меняется, а пустой стимул удаляется из входной очереди: z^(e). Факультативный автомат, кроме этого, при непустом головном стимуле x`¹e в смешанном состоянии v может, не удаляя стимула из входной очереди, совершить посылающий (v,y,v`) или пустой (v,v`) переход. Хотя стимул x` не удаляется из очереди, он, тем не менее, читается и определяет набор допустимых переходов; поэтому z изменяется соответственно: z^(x,y) или z^(x). Дальнейшее поведение автомата определено ╚прочитанным╩ стимулом x` до тех пор, пока этот стимул не будет удален из очереди при совершении принимающего перехода по x`; таким образом, при всех дальнейших срабатываниях автомата, включая этот принимающий переход, автомат не читает головной стимул и никаких стимулов в z не помещается. Если до этого принимающего перехода совершаются посылающие переходы, то только соответствующие реакции помещаются в z.

 

Такое определение сериализации выполнения может показаться странным, особенно для факультативных автоматов. Например, для непустого головного стимула x═ в смешанном состоянии v последовательность переходов (v,y,v₁),(v₁,x,v₂) помещает в сериализацию не (y,x), как можно было бы ожидать, а (x,y). На самом деле, это вполне объяснимо, поскольку стимул x прочитывается первый раз в состоянии v, а не в последующем состоянии v₁, и поскольку прочитанный, но не удаленный из очереди, стимул x уже не может быть изменен и, тем самым, повторное чтение его в состоянии v₁ излишне. Фактически, такой стимул как бы запоминается автоматом, что и происходит явно в тех преобразованиях, которые мы использовали в разделах 2.2-2.4 для моделирования поведения факультативного автомата в смешанных состояниях.

 

Если для входного слова w некоторое выполнение порождает сериализацию z, то, очевидно, yz √ выходное слово при этом выполнении, а xz£w, причем x-подслово конечно xz<w в одном из трех случаев: 1) выполнение заканчивается в терминальном состоянии; 2) начиная с некоторого момента, автомат проходит только через нерецептивные (посылающие) состояния; 3) выполнение заканчивается по ошибке неспецифицированного ввода. При этом само слово z конечно в случаях 1) и 3), а в случае 2) может быть как бесконечным, так и конечным √ если автомат с некоторого момента совершает только пустые переходы в нерецептивных состояниях. Заметим, что последовательность прочитанных автоматом из входной очереди стимулов совпадает с xz, причем все эти стимулы, кроме, быть, может, последнего стимула xz (для конечного xz), удалены из входной очереди, после чего произошел один из указанных трех случаев. Для допустимого входного слова w имеются только первые два случая.

 

Сериализацию z будем называть допустимой (в автомате), если она соответствует некоторому допустимому выполнению, и вполне-допустимой, если она соответствует вполне-допустимому выполнению, то есть, выполнению для допустимого входного слова. Через Z^all обозначим множество допустимых сериализаций, Z(w) -═ множество сериализаций для допустимого входного слова w, а через Z √ подмножество Z^all═ вполне-допустимых сериализаций, которое, для краткости, мы будем называть также z-множеством автомата. Если нужно указать автомат m, будем писать═ Z[m]. Для класса автоматов N будем писать Z[N] ={Z[m] |mÎN}. Заметим, что во множестве всех сериализаций выполнения автомата все допустимые сериализации максимальны (не имеют продолжения, так как бесконечны или заканчиваются в терминальных состояниях), а недопустимые сериализации немаксимальны (заканчиваются в рецептивных состояниях, то есть, могут быть продолжены для другого входного слова). Соответственно, множество Z^all является множеством максимальных сериализаций (антицепью - все допустимые сериализации несравнимы друг с другом).

 

На самом деле, Z может быть определено через Z^all непосредственно. Будем говорить, что входное слово w допустимо во множестве максимальных сериализаций S, если любой начальный отрезок z[1..n] любой сериализации zÎS, x-подслово которого является начальным отрезком w, x(z[1..n])<w, всегда может быть продолжен в S сериализацией z`ÎS, z[1..n]=z`[1..n], такой, что ее x-подслово xz`£w. Сериализацию zÎS будем называть вполне-допустимой в S, если ее x-подслово является начальным отрезком или совпадает с допустимым входным словом. Вполне-допустимым (дуальным) замыканиемS назовем подмножество C<S> всех сериализаций вполне-допустимых в S; замкнутым по вполне-допустимости назовем такое множество S, что C<S>=S. Поскольку вместе с каждой вполне-допустимой сериализацией zÎS вполне-допустима также любая сериализация z`ÎS, x-подслово которой совпадает═ с x-подсловом z, xz`=xz, или является его начальным отрезком xz`£xz, нетрудно показать, что C<C<S>>=C<S>. Будем называть x-подслово сериализации z вполне-допустимого замыкания C<S> максимальным, если оно конечно, но в C<S> не существует сериализации z` с большим x-подсловом xz`>xz. Тогда, очевидно, множество входных слов допустимых в S, которое мы будем обозначать w(S), совпадает с множеством всех бесконечных x-подслов и всех бесконечных продолжений максимальных конечных x-подслов сериализаций вполне-допустимого замыкания C<S>.

 

Для S= Z допустимость входного слова в Z как раз и означает, что при любом выполнении не возникнет ситуации, когда в рецептивном состоянии читается очередной стимул входного слова и для этого стимула не определено поведение автомата. Таким образом, z-множество Z является замыканием по вполне-допустимости множества допустимых сериализаций Z =С(Z^all).

 

Z-множество Z однозначно определяет автоматную словарную функцию W. Словарную функцию для z-множества Z будем обозначать W(Z:

╥        Dom(W(Z))=w(Z)=w(Z^all) √ множество входных слов допустимых в Z (Z^all).

╥        "wÎDom(W(Z)) W(Z)(w)={yz|zÎZ xz£w} √ множество y-подслов сериализаций z-множества, x-подслова которых совпадают с входным словом или являются его начальными отрезками.

 

Будем говорить, что класс автоматов N строго моделируется классом автоматов N`, если Z[N]ÍZ[N`], то есть, для каждого автомата mÎN существует автомат m`ÎN`, имеющий то же z-множество Z[m]=Z[m`]. Если классы автоматов N и N` взаимно строго моделируют друг друга, то есть, множества их z-множеств совпадают Z[N]=Z[N`], то будем говорить, что эти классы автоматов строго эквивалентны. Преобразования разделов 2.2-2.4 сохраняют z-множество, что легко проверяется для каждого преобразования; поэтому═ все доказанные выше эквивалентности классов являются также строгими эквивалентностями.

 

Конечную или бесконечную последовательность смежных переходов (следующий переход начинается в том состоянии, в котором заканчивается предыдущий переход) будем называть маршрутом. (Автомату соответствует граф его состояний, в котором вершины √ это состояния, а дуги, раскрашенные стимулами, реакциями или нераскрашенные - это, соответственно,═ принимающие, посылающие или пустые переходы; последовательности смежных переходов соответствует последовательность смежных дуг, то есть, маршрут в графе.) Маршруту P соответствует последовательность стимулов и реакций его непустых переходов, то есть, сериализация, которую будем называть z-раскраской маршрута и обозначать zP; x-подслово xzP будем называть x-раскраской маршрута, а═ y-подслово yzP - y-раскраской маршрута. Выполнению автомата для данного входного слова w соответствует маршрут, начинающийся в начальном состоянии, который мы будем называть маршрутом выполнения; множество таких маршрутов будем обозначать P(w). Маршрут допустимого выполнения будем называть допустимым маршрутом √ это любой маршрут, начинающийся в начальном состоянии и непродолжаемый, то есть, либо бесконечный, либо заканчивающийся в терминальном состоянии; множество вполне-допустимых маршрутов обозначим P^all. Маршрут вполне-допустимого выполнения будем называть вполне-допустимым маршрутом; множество вполне-допустимых маршрутов обозначим P (если нужно указать автомат m, будем писать P[m]).═ Множество их z-раскрасок zP={zP|PÎP} будем называть z-раскраской автомата.

 

Прежде всего, заметим, что для любого выполнения автомата y-раскраска маршрута выполнения совпадает с y-подсловом сериализации этого выполнения, но x-раскраска маршрута выполнения, вообще говоря, не совпадает с x-подсловом сериализации выполнения, и, тем самым, z-раскраска маршрута выполнения, вообще говоря, не совпадает с сериализацией выполнения. Причина этого в том, что не всякое срабатывание автомата, изменяющее сериализацию, сопровождается переходом. Имеются три типа срабатываний при отсутствии допустимых переходов:

1)      срабатывание в терминальном состоянии (автомат останавливается);

2)      срабатывание в принимающем состоянии при отсутствии e-переходов и пустом головном стимуле (пустой стимул помещается в сериализацию);

3)      срабатывание с фиксацией ошибки неспецифицированного ввода, когда непустой головной стимул недопустим в текущем состоянии: рецептивном √ для императивных автоматов, и принимающем √ для факультативных автоматов.

 

Терминальное срабатывание не изменяет сериализацию, и для допустимых выполнений остается только второй тип срабатывания, который изменяет сериализацию, но не сопровождается переходом. Мы покажем, что можно так преобразовать автомат, сохраняя реализуемое им z-множество Z и, тем самым, словарную функцию W, чтобы таких срабатываний не было, и для такого автомата Z=zP.

 

В следующих разделах мы рассмотрим преобразования, позволяющие перейти сначала к автоматам, в которых сериализация выполнения по допустимому входному слову совпадает с раскраской маршрута выполнения; далее √ к автоматам, в которых все маршруты являются маршрутами таких выполнений, и наконец √ к автоматам, в которых все маршруты имеют уникальную раскраску, то есть, каждая сериализация является раскраской только одного маршрута.

3.2. Три класса автоматов и z-множеств

3.2.1. Класс автоматов A2, в которых z-раскраска совпадает с z-множеством (каждое нетерминальное срабатывание есть переход)

Рассмотрим подкласс A2ÌA автоматов без смешанных состояний, в которых нет срабатываний типа 2. Это означает, что в таком автомате в каждом принимающем состоянии определен хотя бы один e-переход и тогда каждое нетерминальное срабатывание для допустимого выполнения сопровождается переходом. Поэтому каждый допустимый маршрут как последовательность переходов═ взаимно-однозначно соответствует последовательности нетерминальных срабатываний автомата, z-раскраска маршрута zP совпадает с сериализацией выполнения, а z-раскраска автомата совпадает с его z-множеством Z=zP. При этом для допустимого входного слова wÎDom(W) и маршрута выполнения PÎP(w) имеет место xzP£w и yzPÎW(w).

 

Теорема о срабатываниях и переходах: Класс автоматов A строго моделируется своим подклассом A2.

 

Док-во: От срабатываний типа 2 легко избавиться, если в каждом принимающем состоянии v, в котором не определены e-переходы, добавить e-переход (v,e,v), не изменяющий состояния (петлю). Очевидно, что такие преобразования не изменяют z-множество, а получившийся автомат относится к классу A2.

 

Теорема о срабатываниях и переходах доказана.

 

Следствие: поскольку Z(A)=Z(M), A2ÌA и Z(A)ÍZ(A2), очевидно,═ Z(A2) =Z(M).

3.2.2. Класс автоматов A3, в которых все допустимые маршруты (сериализации) вполне-допустимы

В автомате класса A2, вообще говоря, не все допустимые маршруты являются вполне-допустимыми маршрутами. Рассмотрим подкласс A3ÌA2 автоматов, в которых все допустимые маршруты вполне-допустимы.

 

Теорема о вполне-допустимых маршрутах: Класс автоматов A2 строго моделируется своим подклассом A3.

 

Док-во:═ Пусть задан автомат m=(V,v₀,X,e,Y,T) класса A2; мы построим автомат m`, имеющий то же z-множество и принадлежащий классу A3.

 

Для каждого непустого подмножества состояний HÍV построим y-подавтомат yH, переходы которого - это все переходы, принадлежащие маршрутам в m, начинающимся в состояниях из H и содержащим только посылающие и пустые переходы, а состояния - это состояния инцидентные═ таким переходам (являющиеся их началами и концами). Множество H будем называть множеством входных состоянийy-подавтомата yH. Через tH обозначим множество состояний y-подавтомата, являющихся принимающими в m; это множество состояний y-подавтомата будем называть его множеством выходных состояний. Полученные y-подавтоматы, как подавтоматы одного автомата, имеют общие состояния и переходы. Нам нужно "расклеить" их, превратив в y-автоматы с непересекающимися множествами состояний и переходов. Поэтому для каждого y-подавтомата yH определим соответствующий y-автомат (yH,H), получающийся переименованием состояний: каждое состояние v из y-подавтомата yH в y-автомате (yH,H) обозначим как (v,H).

 

Автомат m` строится как объединение всех y-автоматов автомата m, в которое добавлены дополнительные принимающие переходы следующим способом (рис.3.2.1):

1)      Для каждого y-подавтомата yH и каждого стимула x (пустого или непустого), допустимого в автомате m в каждом выходном состоянии y-подавтомата, определяется множество R(H,x) принимающих переходов, начинающихся в этих выходных состояниях.

2)      Для множества H` концов переходов из R(H,x) рассматривается y-подавтомат yH`.

3)      Для каждого перехода (v,x,v`)ÎR(H,x) в автомате m` добавим переход ((v,H),x,(v`,H`)) из выходного состояния (v,H) y-автомата (yH,H) во входное состояние (v`,H`) y-автомата (yH`,H`).

4)      Начальным состоянием автомата m` объявим состояние (v₀,{v₀}) y-автомата (y{v₀},{v₀}) (соответствующий y-подавтомат порождается одним начальным состоянием {v₀} автомата m).

5)      После этого оставляем в автомате m` только те состояния, которые достижимы из начального состояния (v₀,{v₀}), и только те переходы, которые определены в достижимых состояниях.

 

Рис.3.2.1

 

По построению видно, что автомат m` обладает всеми нужными свойствами.

 

Теорема о допустимых маршрутах доказана.

 

Замечание: На рис. 3.2.1 не показаны e-петли, определенные в каждом принимающем состоянии. С учетом этих петель выделяются еще два y-автомата: (y{2,3},{2,3}) и (y{0,2,3},{0,2,3}), в которых вход совпадает с выходом, во все их состояния ведут e-переходы из всех копий принимающих состояний 0,2,3 во всех y-автоматах и во всех состояниях этих y-графов определены принимающие переходы по стимулу x во входное состояние y-графа (y{0},{0}). В этом автомате существует недопустимый бесконечный маршрут 0¾x╝1,(1¾y₂╝3,3¾x₁╝1)^w (этот маршрут является маршрутом выполнения только для одного слова x(x₁)^w, однако это слово недопустимо, поскольку для него имеется другой маршрут выполнения 0¾x╝1,1¾y₁╝2, заканчивающийся по ошибке неспецифицированного ввода: в состоянии 2 стимул x₁ недопустим).

 

Следствие: поскольку Z(A2)=Z(A)=Z(M), A3ÌA2 и Z(A2)ÍZ(A3), очевидно,═ Z(A3)=Z(M).

═

Выше мы уже говорили, что поскольку автомат с некоторого момента может прекратить выборку стимулов из входной очереди, x-подслово сериализации может не совпадать со входным словом, а являться его начальным отрезком. Теперь мы можем показать, что неравенство xz<w для сериализации z выполнения по некоторому допустимому входному слову w и конечность x-раскраски маршрута PÎP(w), xzP<w носят принципиальный характер. Если выполнение заканчивается в терминальном состоянии v (сериализация и маршрут конечны), то этот случай легко обойти, преобразовав автомат с сохранением словарной функции (правда, без сохранения сериализаций): для этого достаточно сделать состояние v принимающим, определив в нем переходы-петли (v,x`v) для всех стимулов x`ÎX`. Однако, другой случай, когда выполнение бесконечно, но с какого-то момента проходит только через нерецептивные состояния (маршрут бесконечен), обойти не удается. Мы покажем, что для некоторых словарных функций любой реализующий их конечный автомат выбирает из входной очереди лишь конечное число стимулов для некоторых допустимых входных слов.

 

Теорема о конечном x-подслове сериализации: Существуют такие автоматные словарные функции, что в любом конечном автомате, их реализующем, имеется вполне-допустимое выполнение с конечным x-подсловом сериализации.

 

Док-во: Примером может служить словарная функция автомата класса A3, изображенного на рис. 3.2.2: e^w╝(), e*x(e*x)ⁿe^w╝{y^w,y*y₁ⁿ}, (e*x)^w╝{y^w,y*y₁^w}, где n=0.. - число зависимых повторений - все вхождения n в показателе степени указывают на одно и то же число повторений n, "*" - как обычно, независимое число повторений ноль или более раз.

Рис.3.2.2

 

Допустим, существует автомат, реализующий эту словарную функцию, в котором все вполне-допустимые сериализации имеют бесконечные x-подслова. Тогда, очевидно, существует такой же автомат класса A3, и в нем все допустимые маршруты имеют бесконечные x-подслова. Заметим, что, согласно словарной функции, входное слово x^w может быть отображено в выходное слово y^w. Отсюда следует, что в автомате есть бесконечный допустимый маршрут P такой, что xzP=x^w и yzP=y^w. Тогда существует циклический маршрут C, все переходы которого - это принимающие переходы по стимулу x или посылающие переходы с реакцией y, причем число и тех и других в маршруте C больше нуля. Также должен существовать конечный маршрут N, начинающийся в начальном состоянии и заканчивающийся в начальном состоянии цикла C. В автомате класса A3 в принимающих состояниях определены e-переходы. Пусть такой e-переход определен в состоянии, в котором определен принимающий переход C[i], и пусть E - произвольный маршрут, начинающийся этом состоянии, содержащий только посылающие, пустые и e-переходы (не содержащий x-переходов) и бесконечный или заканчивающийся в терминальном состоянии. Рассмотрим допустимый маршрут P1=N^C^C[1..i-1]^E. В нем, очевидно, конечное ненулевое число принимающих переходов по стимулу x. Тогда, в соответствии со словарной функцией, в нем должно быть конечное число посылающих переходов по реакции y₁; пусть это число равно n. Тогда рассмотрим допустимый маршрут Pn=N^Cⁿ⁺²^C[1..i-1]^E. В нем, очевидно, конечное число N³n+2 принимающих переходов по стимулу x. Очевидно, N-1>n. Тогда, в соответствии со словарной функцией, в нем должно быть N-1 посылающих переходов по реакции y₁, но, поскольку C не содержит y₁-переходов, маршрут Pn должен содержать столько же y₁-переходов, сколько их содержит маршрут P1, то есть, n, чего не может быть, поскольку N-1>n . Мы пришли к противоречию и, тем самым, утверждение доказано.

 

Теорема о конечном x-подслове сериализации доказана.

3.2.3. Класс автоматов A4 с детерминированным z-множеством

Распространим понятие регулярности [7-9] на множества не только конечных, но и бесконечных слов. Пусть задан некоторый алфавит символов A.═ Порождающим графом будем называть граф G с выделенными начальными и конечными вершинами, некоторые дуги которого раскрашены символами из A. Маршрут в графе G имеет раскраску как последовательность раскрасок его раскрашенных дуг (нераскрашенные √ пустые √ дуги пропускаются). Порождающий маршрут √ маршрут, начинающийся в начальной вершине и бесконечный или заканчивающийся в конечной вершине. Будем говорить, что граф G порождает множество раскрасок всех порождающих маршрутов графа. Множество слов H в алфавите A будем называть регулярным, если оно порождается некоторым конечным порождающим графом.

 

Порождающий граф G будем называть детерминированным, если из каждой его вершины выходит не более одной дуги, раскрашенной данным символом из алфавита A. Конечный детерминированный порождающий граф будем называть нормальным, если он имеет одну начальную вершину, не имеет пустых дуг и все вершины достижимы из начальной вершины. Очевидно, в нормальном порождающем графе все порождающие маршруты имеют разные раскраски, то есть, каждое слово из порождаемого множества порождается ровно одним маршрутом. Аналогично случаю регулярных множеств конечных слов, можно сформулировать следующую теорему:

 

Теорема о нормальном порождающем графе: Каждое регулярное множество слов порождается нормальным порождающим графом.

 

Док-во: Пусть задан произвольный конечный порождающий граф G; мы построим нормальный порождающий граф G`, порождающий то же множество слов. Прием его построения похож на соответствующий прием для порождающих графов регулярных множество конечных слов [7,9].

 

Этап1. Прежде всего, заметим, что, если в вершине v, достижимой из какой-нибудь начальной вершины, начинается маршрут, состоящий только из пустых дуг и бесконечный или заканчивающийся в конечной вершине графа G, то вершину v можно пометить как конечную без изменения порождаемого множества слов. Проделаем эту процедуру для всех таких вершин v.

 

Этап 2. Далее вершинами графа G` объявим все непустые подмножества вершин графа G. Для каждого подмножества вершин U и каждого символ a рассмотрим конечный маршрут, начинающийся в некоторой вершине из U, все дуги которого нераскрашены, кроме одной, раскрашенной символом a. Если такие маршруты есть и H √ множество их концов, то проведем дугу (U,x,H) из U в H раскрашенную символом a. Начальной вершиной графа G` объявим множество всех начальных вершин графа G. Конечными вершинами графа G` объявим все множества, содержащие хотя бы одну конечную вершину графа G. После этого удалим из G` все его вершины, недостижимые из начальной, и все инцидентные им дуги. Полученный граф является нормальным по построению (рис. 3.2.3).

 

Рис.3.2.3

Поскольку дуге (U,a,H) графа G` взаимно-однозначно соответствует непустое множество всех конечных маршрутов графа G, начинающихся в вершинах из U и имеющих раскраску (a), то и любому маршруту P` графа G`, начинающемуся в вершине U взаимно-однозначно соответствует непустое множество всех маршрутов графа G, начинающихся в вершинах из U и имеющих такую же раскраску, что и P`. Поскольку начальная вершина G` есть множество начальных вершин G, а конечная вершина G` содержит конечную вершину графа G (включая добавленные на этапе 1), порождающему маршруту графа G`, очевидно, взаимно-однозначно соответствует непустое множество всех порождающих маршрутов графа G, имеющих ту же раскраску.

 

Теорема о нормальном порождающем графе доказана.

 

В автомате класса A3 все допустимые маршруты вполне-допустимы. Поэтому, если в графе состояний такого автомата конечными вершинами объявить терминальные вершины, то такой граф является порождающим графом в объединенном алфавите стимулов (включая пустой стимул) и реакций X`ÈY, а порождаемое им регулярное множество является z-множеством автомата. Однако, в общем случае, этот порождающий граф недетерминирован, то есть, может существовать несколько разных допустимых маршрутов, имеющих одну и ту же z-раскраску. Заметим, что детерминированность графа состояний как порождающего графа вовсе не означает детерминированности автомата: все принимающие переходы, определенные в данном состоянии, отличаются стимулами и поэтому при данном головном стимуле возможен только один принимающий переход; однако, хотя все посылающие переходы, определенные в данном состоянии, отличаются реакциями, допустим любой из них и выбор посылающего перехода, то есть, посылаемой реакции, по-прежнему недетерминирован. Классом A4ÌA3 назовем подкласс, в котором все допустимые маршруты имеют уникальные z-раскраски, то есть, граф состояний которого является детерминированным порождающим графом. Будем говорить, что такие автоматы - это автоматы с детерминированным z-множеством. Более строго, следовало бы говорить о мульти-множестве сериализаций (маршрутов) √ множестве с повторяющимися элементами, где каждая сериализация (раскраска маршрута) повторяется столько раз, скольким выполнениям (маршрутам) она соответствует; детерминированное мультимножество √ это обычное множество, где каждый элемент повторяется один раз.

 

Теорема о детерминированном z-множестве: Каждый автомат класса A3 строго моделируется некоторым автоматом класса A4.

 

Док-во: Пусть задан автомат m класса A3, мы построим автомат m`, имеющий ту же z-раскраску и принадлежащий классу A4.

 

Этап 1. Граф состояний автомата m можно рассматривать как порождающий граф, конечными вершинами которого являются терминальные состояния. Заметим, что порождающие маршруты совпадают в этом случае с допустимыми маршрутами. Для этого графа построим нормальный порождающий граф.

 

Этап 2. В полученном графе могут появиться конечные вершины, не являющиеся терминальными. Чтобы избавиться от них, из каждой такой вершины v проведем пустую дугу в какую-нибудь терминальную вершину (если таких нет, добавим новую терминальную вершину) и объявим вершину v не конечной. Очевидно, порождаемое множество от этого не изменится, а граф останется детерминированным порождающим графом (хотя уже и не нормальным).

 

Этап 3. В полученном графе могут быть смешанные вершины. Чтобы избавиться от них, для каждой смешанной вершины v добавим новую вершину v₁ и пустую дугу (v, v₁), а каждую принимающую дугу, ведущую из v, (v,x,v`), где xÎX`, заменим на принимающую дугу из v₁ - (v₁,x,v`). Вершина v будет теперь посылающей, а вершина v₁ - принимающей (рис.3.2.4). Раскраски маршрутов, очевидно, не изменились (добавленные пустые дуги не участвуют в раскраске маршрута) и граф остался детерминированным порождающим графом.

═

Рис.3.2.4

 

Этот граф будем считать графом состояний автомата m`. По построению он относится к классу A2 (нет смешанных состояний и в каждом принимающем состоянии определен e-переход, поскольку так было в m). По построению, множествам всех одинаково раскрашенных допустимых маршрутов в m взаимно-однозначно соответствуют так же раскрашенные допустимые маршруты в m`, то есть,═ Z^all[m`]= Z<sup>all</sup>[m]. Поскольку m относится к классу A3, в нем все допустимые маршруты вполне-допустимы Z[m]=C<Z<sup>all</sup>[m]>=Z<sup>all</sup>[m], поэтому Z[m`]=C<Z^all[m`]>=С<Z<sup>all</sup>[m]>=Z<sup>all</sup>[m`] и Z[m`]=Z[m], то есть, автомат m` тоже относится к классу A3 и имеет то же z-множество, что m. Из детерминизма порождающего графа следует детерминированность z-множества в m`, то есть, m` относится к классу A4.

═

Теорема о детерминированном z-множестве доказана.

3.3. Автоматные множества сериализаций, распознающие и отвергающие автоматы.

Множество S сериализаций будем называть автоматным, если оно является z-множеством некоторого автомата. Выше уже показано, что автоматное множество регулярно, и для того, чтобы регулярное множество было автоматным, нужно, чтобы оно было замкнуто по вполне-допустимости C<S> = S и любой начальный отрезок сериализации, продолжаемый в ней стимулом, мог быть также продолжен═ пустым стимулом (допустимость пустых стимулов во всех рецептивных состояниях). Таким образом, мы имеем следующую теорему.

 

Теорема об автоматности множества сериализаций: Необходимым и достаточным условием автоматности множества S сериализаций является выполнение следующих трех требований:

╥        Регулярность: Множество S регулярно.

╥        Допустимость x-подслов: Все x-подслова сериализаций из S допустимы в S, что эквивалентно замкнутости S по вполне-допустимости C<S> = S.

╥        Допустимость пустого стимула: Для любой сериализации zÎS═ любой ее начальный отрезок u<z, непосредственно предшествующий стимулу z[nu+1]ÎX`, где nu √ длина u, может быть продолжен пустым стимулом, то есть, существует z`ÎS такая, что ue<z`.

 

С точки зрения тестирования, представляет интерес вопрос: существует ли автомат, который, имея во входной очереди сериализацию, определяет, может или не может она принадлежать z-множеству заданного автомата. Поскольку речь идет не только о конечных, но и о бесконечных словах, мы в общем случае не можем говорить о распознающих автоматах, то есть, автоматах, которые определяли бы принадлежность слова множеству за конечное число шагов, то есть, по его начальному отрезку конечной длины. Например, автомат на рис.3.3.2 имеет сериализацию xy^wÎZ, каждый начальный отрезок которой xyⁿ является начальным отрезком сериализации xyⁿy₁^wÏZ. Заметим, что для множеств конечных слов распознаваемость совпадает с регулярностью: по нормальному порождающему графу легко построить граф состояний распознающего автомата, а по графу состояний распознающего автомата √ порождающий граф.

 

Рис.3.3.2

 

С другой стороны, мы можем говорить об отвергающих автоматах, которые за конечное число шагов отвергают слово, если оно не принадлежит множеству, хотя для слов, принадлежащих множеству, могут работать бесконечно.

 

Будем говорить, что автомат m является отвергающим автоматом для множества слов S в алфавите A, если

╥        алфавит стимулов автомата m - это алфавит A;

╥        алфавит реакций состоит из одной реакции "не принадлежит";

╥        для каждого слова zÎS автомат m выдает единственное пустое выходное слово,

╥        для каждого слова zÏS автомат m выдает единственное выходное слово, состоящее из одной реакции "не принадлежит".

 

Отвергающий автомат будем называть нормальным, если он детерминирован (как автомат, а не как порождающий граф) и не имеет пустых переходов.

 

Теорема об отвергающем автомате: Множество слов регулярно тогда и только тогда, когда для него существует нормальный отвергающий автомат.

 

Док-во: По нормальному порождающему графу регулярного множества слов H в алфавите A можно построить граф состояний нормального отвергающего автомата для H:

╥        алфавитом стимулов объявляется алфавит A;

╥        алфавитом реакций объявляется множество из одной реакции "не принадлежит";

╥        начальным состоянием объявляется состояние автомата, соответствующее начальной вершине порождающего графа;

╥        добавляются два состояния t и t` и посылающий переход из t в t` с реакцией "не принадлежит";

╥        если из какой-то вершины v порождающего графа не выходит дуга, помеченная некоторым символом a из A, в соответствующем состоянии v автомата определим принимающий переход по стимулу a в состояние t, то есть, переход (v,a,t).

 

Наоборот, если задан нормальный отвергающий автомат для множества слов H в алфавите A, то по его графу состояний можно построить нормальный порождающий граф для множества H. В графе состояний автомата выполним следующие преобразования:

╥        удаляются вершины, являющиеся началами посылающих дуг с реакцией "не принадлежит", и все инцидентные им дуги;

╥        если при этом образуются новые терминальные вершины, то эти вершины удаляются═ вместе с инцидентными им дугами (старые терминальные вершины остаются) - это повторяется до тех пор, пока остаются новые терминальные вершины;

╥        удаляются все вершины, не достижимые из начальной вершины, и все дуги им инцидентные.

 

Теорема об отвергающем автомате доказана.

 

Для словарной функции W═ можно говорить об отвергающем автомате, который имеет две входные очереди, в которые помещаются входное слово w и выходное слово u, и одну выходную очередь, в которую автомат должен поместить вердикт "не принадлежит", если wÏDom(W) или uÏW(w), а в противном случае - ничего. Если для словарной функции существует такой отвергающий автомат, будем называть ее регулярной. Можно сформулировать следующие нерешенные задачи:

1.      Всякая ли автоматная словарная функция (быть может, с некоторыми дополнительными условиями) регулярна?

2.      Всякая ли регулярная словарная функция (быть может, с некоторыми дополнительными условиями) автоматна?

3.4. Квази-конечные сужения словарной функции и z-множества

Мы определили словарную функцию как функцию на бесконечных входных словах, поскольку это было удобной математической абстракцией. Однако, при тестировании мы можем иметь дело только с конечными входными словами. В этой математической абстракции конечное входное слово можно понимать как бесконечное слово, в котором имеется только конечное число непустых стимулов; такие бесконечные слова будем называть квази-конечными.

 

Квази-конечным сужением словарной функции W будем называть функцию W|_F, определенную только на квази-конечных входных словах:

╥        Dom(W|_F) = (X`^*^{e^w})ÇDom(W)

╥        "wÎDom(W|_F) W|_F(w)=W(w)

 

Соответственно, квази-конечным сужением множества сериализацийS (в частности, z-множества автомата Z) будем называть его подмножество S|_F, содержащее только такие сериализации, x-подслова которых конечны или квази-конечны. Для произвольного множества слов U через U[] будем обозначать множество начальных отрезков конечной длины слов из U; это множество будем называть конечным сужением множестваU.

 

Прежде всего, зададимся вопросом: однозначно ли определяется словарная функция автомата по ее квази-конечному сужению?

 

Ответ на этот вопрос отрицательный. Пример приведен на рис.3.4.1.═ Для двух автоматов 1 и 2 значение словарной функции на всех допустимых квази-конечных словах одно и то же √ реакция y. Однако, полные словарные функции (на всех бесконечных словах)═ автоматов 1 и 2 различаются: при непрерывной (без пустых стимулов) подаче на автомат стимула x, автомат 1 ничего не выдает (пустое выходное слово), а автомат 2 по-прежнему выдает реакцию y.

 

Рис.3.4.1

 

В этой ситуации у нас возможны три направления дальнейшего движения:

1.      Можно ограничиться такими классами автоматов, для которых словарная функция однозначно определяется ее квази-конечным сужением. Для этого надо описать класс словарных функций, однозначно определяемых своими квази-конечными сужениями.

2.      Можно ограничиться такими классами автоматов, для которых нас не интересует их поведение на бесконечных входных словах. Иными словами, функциональные требования к автомату могут быть сформулированы в терминах квази-конечного сужения словарной функции. Тем самым, мы будем проверять поведение автомата только на квази-конечных входных словах и, если на таких словах оно правильно, то будем делать вывод, что реализация соответствует модели.

3.      Если функциональные требования к автомату не могут быть сформулированы только в терминах квази-конечного сужения словарной функции, то добавим дополнительные функциональные требования.

 

Третье направление нуждается в разъяснениях. Здесь есть две проблемы:

1.      Как задавать дополнительные функциональные требования?

2.      Как проверять дополнительные функциональные требования при тестировании только на квази-конечных входных словах?

 

Приведенный пример автоматов 1 и 2, словарные функции которых различны, но имеют одинаковое квази-конечное сужение, показывает, что эти автоматы имеют разные z-множества. Например, любая сериализация в автомате 2 имеет на второй позиции реакцию y, а в автомате 1 √ реакция y располагается непосредственно после первого пустого стимула. Это наталкивает на мысль формулировать дополнительные функциональные требования в терминах ограничений на вполне-допустимые сериализации автомата, то есть, в виде предиката на множестве всех сериализаций для данных алфавитов стимулов и реакций. Имея в виду проблему проверяемости этих дополнительных требований, нас интересуют в первую очередь предикаты на конечных сериализациях, интерпретируемых как начальные отрезки сериализаций автомата, то есть, элементы конечного сужения z-множества. Автоматы 1 и 2 в нашем примере различаются по начальным отрезкам сериализаций длины 2.

3.5. Предикат на конечных сериализациях

Слово (в некотором алфавите) w называется (индуктивным) пределом═ неубывающей бесконечной последовательности конечных слов u[1]£u[2]£..., если для каждого i=1.. u[i]£w и для любого другого слова w`, обладающего тем же свойством, w£w`. Существование предела очевидно: если, начиная с некоторого i все последовательности u[j] (j³i) равны, w=u[i]; в противном случае последовательность длин слов u[i] бесконечно возрастает и для любого n=1.. все слова, начиная с первого в последовательности слова, длина которого не меньше n, содержат один и тот же символ в позиции n, который и определим как n-ый символ слова w. Предел последовательности, очевидно, единственный.

 

Множество всех═ неубывающих бесконечных последовательностей начальных отрезков слов множества U будем называть множеством его пределов и обозначать Lim(U). Замыканием по пределу множества слов U назовем его объединение с множеством его пределов и обозначать L<U> = UÈLim(U). Множество назовем замкнутым, если оно совпадает со своим замыканием: U=L<U>. Очевидно, не всякое множество замкнуто: например, множество всех слов в алфавите {0,1}, каждое из которых содержит ровно одну 1, незамкнуто, так как не содержит нулевое слово, являющееся пределом последовательности 0<00<000<… начальных отрезков слов 010…, 0010…, 00010….

 

Если множество U незамкнуто по пределу, то отвергающий автомат не существует. Действительно, если существует═ возрастающая бесконечная последовательность w₁[1..n₁]<w₂[1..n₂]<... начальных отрезков слов из U, wiÎU для i=1..., предел которой wÏU, то, очевидно, слово w не может быть отвергнуто ни по какому своему начальному отрезку (конечной длины), поскольку такой отрезок является одновременно начальным отрезком некоторого слова w_i, принадлежащего U. Конечно, поскольку не всякое замкнутое множество регулярно, не для всякого замкнутого множества существует отвергающий автомат. Например, множество, состоящее из одного слова, являющегося десятичной записью иррационального числа, замкнуто, но не регулярно, и отвергающего автомата для него не существует. Однако, для всякого регулярного множества отвергающий автомат существует и поэтому оно замкнуто. В частности,═ z-множество автомата замкнуто: L<Z> = Z.

 

Заметим, что, используя понятие замыкания по пределу, мы могли бы определить регулярное множество (как конечных, так и бесконечных) слов U как объединение некоторого регулярного множества конечных слов F₁ и множества пределов некоторого другого регулярного множества═ конечных слов F₂: U=F₁ÈLim(F₂), где F₁ содержит все конечные слова из U, а Lim(F₂) содержит все бесконечные слова из U. Порождающий граф для F₁═ совпадает с порождающим графом для U, а порождающий граф для F₂═ строится из него добавлением конечных вершин на каждом циклическом маршруте, на котором конечных вершин нет.

 

Очевидно, L<U> Í L<U[]>, причем равенство достигается тогда и только тогда, когда все конечные слова в U максимальны в нем, то есть, U - антицепь.

 

Множество U идеально, если вместе с каждым словом оно содержит и все его начальные отрезки. Идеальность множества U═ конечных слов эквивалентна тому, что U является конечным сужением некоторого множества H, то есть, U=H[]. В частности, в качестве такого множества H можно всегда выбрать замыкание по пределу H=L<U>. Заметим, однако, что конечное сужение незамкнутого по пределу множества также идеально. Очевидно также, что U совпадает с конечным сужением множества пределов U=Lim(U)[]=Lim(H)[]. Если U √ это множество сериализаций, то множество пределов будет множеством максимальных сериализаций, для которого определено понятие допустимого входного слова, и поэтому мы можем говорить о входных словах, допускаемых во множестве пределов w(Lim(U))=w(Lim(H)).

 

Пусть на множестве всех конечных сериализаций (для данных алфавитов стимулов и реакций) задан предикат p. Обозначим индуцируемое предикатом множество сериализаций U(p)={u|p(u)=true}. Будем считать, что U(p) идеально. Входное слово, допустимое во множестве пределов U(p), будем называть допускаемым предикатом. Определим индуцируемое предикатом p семейство автоматов A(p) следующим образом: mÎA(p) тогда и только тогда, когда выполняются следующие два свойства:

1.      Каждое входное слово допускаемое предикатом допустимо в автомате:
w(Lim(U(p))) Í Dom(W[m])[].

2.      Если x-подслово начального отрезка вполне-допустимой сериализации автомата совпадает с x-подсловом некоторой сериализации из U(p), то сам этот отрезок принадлежит U(p): {uÎZ[m][] | xuÎxU(p)} Í U(p).

 

Следует отметить, что индуцируемые автоматы определяются с точностью до их вполне-допустимых сериализаций, то есть, два автомата с одним z-множеством либо оба не попадают, либо оба попадают в индуцируемое семейство A(p). Поэтому можно говорить об индуцируемом семействе z-множеств.

 

Пусть заданы два множества максимальных сериализаций H и U. Будем говорить, что множество H сводимо к множеству U, если 1) каждое входное слово, допустимое в U, допустимо в H, 2) каждая вполне-допустимая сериализация H, x-подслово которой является начальным отрезком или совпадает с входным словом допустимым в U, принадлежат U. Будем также говорить, что множество H конечно-сводимо к множеству U, если 1) каждый начальный отрезок входного слова допустимого в U является начальным отрезком входного слова допустимого в H, 2) каждый начальный отрезок вполне-допустимой сериализации H, x-подслово которого является начальным отрезком входного слова, допустимого в U, является начальным отрезком вполне-допустимой сериализации U.

 

Предикат p индуцирует конечное сужение множества максимальных сериализаций U=Lim(U(p)), то есть, U(p)=U[], и, очевидно, индуцируемое предикатом семейство z-множеств является семейством всех z-множеств, конечно-сводимых к U.

═

Лемма о сводимом множестве сериализаций: Если множество максимальных сериализаций H сводимо к множеству максимальных сериализаций U, то оно конечно-сводимо к нему.

 

Док-во:═ Действительно, поскольку каждое входное слово w, допустимое в U, допустимо в H, то каждый его начальный отрезок u<w является начальным отрезком входного слова w, допустимого в H. Если начальный отрезок z₁ сериализации z, вполне-допустимой в H, имеет x-подслово xz₁, являющееся начальным отрезком входного слова w, допустимого в U, xz₁<w, то это входное слово w допустимо также в H. Отсюда следует, что в H имеется сериализация z`, соответствующая w, xz`£w, являющаяся продолжением отрезка z₁<z`. Но тогда z` принадлежит также U и, следовательно, ее начальный отрезок z₁ является начальным отрезком сериализации z`, вполне-допустимой в U.

 

Лемма о сводимом множестве сериализаций доказана.

 

Лемма о конечно-сводимом множестве сериализаций: Если замкнутое по пределу множество максимальных сериализаций H конечно-сводимо к замкнутому по пределу множеству максимальных сериализаций U, то оно сводимо к нему.

 

Док-во:═ Действительно, из замкнутости по пределу множества H следует замкнутость по пределу множества допустимых в нем входных слов. Поскольку каждое входное слово w допустимое в U может быть представлено как предел бесконечной═ неубывающей последовательности своих начальных отрезков, а все такие отрезки являются также отрезками входных слов, допустимых в H, то такую же последовательность отрезков мы имеем в H и, в силу замкнутости по пределу множества входных слов, допустимых в H, входное слово w допустимо также и в H. Cериализация z, вполне-допустимая в H, x-подслово которой является начальным отрезком или совпадает с входным словом, допустимым в U, может быть представлена как предел бесконечной═ неубывающей последовательности своих начальных отрезков, а все такие отрезки являются также отрезками сериализаций, вполне-допустимых в U, то такую же последовательность отрезков мы имеем в U и, в силу замкнутости U по пределу, сериализация z допустимо в H.

 

Лемма о конечно-сводимом множестве сериализаций доказана.

 

Ниже мы рассмотрим два вида предикатов конечных сериализаций.

 

3.5.1. Предикат z-множества

Предикатом z-множества p(Z) будем называть предикат, индуцирующий конечное сужение этого z-множества: U(p(Z)) = Z[]. Иными словами, предикат z-множества индуцирует множество начальных отрезков вполне-допустимых сериализаций некоторого автомата с данной словарной функцией W(Z).

 

Будем говорить, что автомат m сводим к z-множеству Z, если к нему сводимо z-множество автомата Z[m], то есть, 1) каждое входное слово, допустимое в Z, допустимо в m, Dom(W(Z)) Í Dom(W[m]) и 2) каждая вполне-допустимая сериализация автомата, x-подслово которой является начальным отрезком или совпадает с входным словом допустимым в Z, принадлежит Z, "wÎDom(W(Z)) {zÎZ[m] | xz£w} Í Z.

 

Из Леммы о сводимом множестве сериализаций следует, что автомат m сводимый к z-множеству Z принадлежит семейству автоматов, индуцируемых предикатом z-множества: mÎA(p(Z)). Поскольку все z-множества замкнуты по пределу, из Леммы о конечно-сводимом множестве сериализаций следует, что автомат m из семейства автоматов, индуцируемых предикатом z-множества Z, сводим к этому к z-множеству. Итак, нами доказана следующая

 

Теорема о предикате z-множества: Предикат z-множества индуцирует семейство всех автоматов, сводимых к этому z-множеству.

3.5.2. Предикат словарной функции

Теорема о предикате z-множества позволяет ограничиться тестированием только конечных сериализаций, однако при этом мы проверяем соответствие реализации модели не по словарной функции, а по z-множеству. Иными словами, мы начинаем различать реализации, имеющие одну и ту же, заданную моделью, словарную функцию, но разные z-множества, несводимые к одному, задаваемому предикатом. Поэтому теперь попробуем перейти к рассмотрению множества автоматов, реализующих данную словарную функцию безотносительно к их z-множествам. Для этого мы будем рассматривать z-множество словарной функции Z(W)={Z|W(Z)=W} √ как объединение z-множеств с данной словарной функцией. Соответственно, речь пойдет о предикате словарной функции p(W), который индуцирует множество U(p(W))=Z(W)[]=È{Z[]|W[Z]=W} начальных отрезков вполне-допустимых сериализаций не одного, а всех автоматов с данной словарной функцией W. Нас будет интересовать замкнутость, регулярность и существование отвергающего автомата, который по начальному отрезку (конечной длины) сериализации определяет, может или не может она принадлежать z-множеству какого-нибудь автомата, реализующего данную словарную функцию W.

 

Лемма о первой реакции в сериализации: Для любой автоматной словарной функции W, любого допустимого входного слова xÎDom(W), любого соответствующего ему выходного слова yÎW(w) и любого натурального числа n существует автомат m класса A3, реализующий эту словарную функцию W[m]=W, в котором одна из сериализаций для пары (x,y) не содержит реакций на первых n позициях, то есть, хотя бы для одного маршрута P такого, что xzP£x и yzP=y, первые n переходов принимающие.

 

Док-во: Будем вести доказательство от противного и в терминах графа состояний (рис.3.5.1). Пусть существует такая словарная функция W, такое допустимое входное слово xÎDom(W), такое соответствующее ему выходное слово yÎW(x) и такое натуральное число n, что в каждом автомате m класса A3, реализующем эту словарную функцию W[m]=W, для каждого маршрута P, раскраски которого xzP£x и yzP=y, отрезок P[1..n] содержит посылающий переход. Выберем для данных W, x и y число n минимальным и выберем автомат m класса A3 и в нем маршрут P такой, что xzP£x и yzP=y, отрезок P[1..n-1] содержит только принимающие переходы, а переход P[n] посылающий. Очевидно, zP[1..n]=x[1..n-1]^y[1].

 

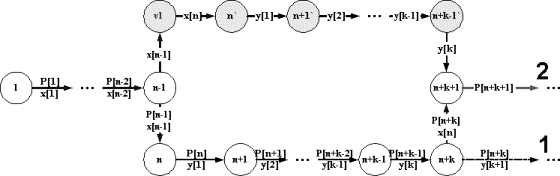
Рис.3.5.1

 

Маршрут P[n..] либо 1) не содержит принимающих дуг, либо 2) содержит первый принимающий переход P[n+k] (k>0) такой, что (zP)[n+k]=x[n]. Рассмотрим подавтомат m`, содержащий в случае 1) - все переходы оставшейся части маршрут P[n..], а в случае 2) - все переходы отрезка маршрута P[n..n+k-2] (при k=1, маршрут нулевой - только одно состояние - начало n-ого перехода маршрута P), а также все инцидентные им состояния. Скопируем этот подавтомат m` (его переходы и состояния для отличения от переходов и состояний автомата m будем снабжать штрихом "`"). Введем новое состояние v1, и добавим для состояния - начала перехода P[n-1] принимающий переход по стимулу x[n-1] в состояние v1, а в состоянии v1 добавим принимающий переход по стимулу x[n] в состояние-копию начала перехода P[n]`. Для случая 1) построение закончено, а для случая 2) добавим для состояния-копии начала перехода P[n+k-1]` посылающий переход по реакции y[k] в состояние √ начало перехода P[n+k+1].

 

Тем самым, мы добавили маршрут с z-раскраской, в которой n-ый стимул входного слова x[n] принимается непосредственно после приема n-1-го стимула, а потом уже выдается первая реакция y[1]: для случая 1) мы для маршрута с z-раскраской x[1],...,x[n-2],x[n-1],y[1],... добавили маршрут с z-раскраской x[1],...,x[n-2],x[n-1],x[n],y[1],..., а в случае 2) мы для маршрута с z-раскраской x[1],...,x[n-2],x[n-1],y[1],...,y[k],x[n],... добавили маршрут с z-раскраской x[1],...,x[n-2],x[n-1],x[n],y[1],...,y[k],..... Таким образом, мы построили автомат, который, очевидно, реализует ту же словарную функцию, но имеет вполне-допустимый маршрут, z-раскраска которого имеет стимулы на первых n позициях, то есть, не содержит реакции на первых n позициях, что противоречит предположению.

 

Лемма о первой реакции в сериализации доказана.

 

Словарную функцию W будем называть существенно ненулевой, если хотя бы для одного допустимого входного слова wÎDom(W) множество выходных слов не содержит пустого выходного слова ()ÏW(w), что эквивалентно wÏZ(W).

 

Теорема о незамкнутости z-множества словарной функции: Если автоматная словарная функция W═ существенно ненулевая, то ее z-множество Z(W) незамкнуто.

 

Док-во: Если словарная функция существенно ненулевая, то, очевидно, само слово w, для которого ()ÏW(w), не принадлежит z-множеству никакого автомата, реализующего эту словарную функцию. Однако, согласно Лемме о первой реакции в сериализации, первая реакция в сериализации z для входного слова w (xz£w)может быть сколь угодно поздно, то есть, любой начальный отрезок w может быть начальным отрезком z. Таким образом, слово wÏZ(W), но любой его начальный отрезок конечной длины имеет в Z(W) продолжение, то есть, Z(W) незамкнуто.

 

Теорема о незамкнутости z-множества словарной функции доказана.

 

Будем говорить, что автомат m сводим к словарной функции W, если 1) Dom(W[m]) Í Dom(W) и 2) "wÎDom(W[m])═ W[m](w) Í W(w). Очевидно, сводимость автомата к словарной функции эквивалентна его сводимости к z-множеству словарной функции. Из Леммы о сводимом множестве сериализаций следует, что семейство автоматов, индуцируемое предикатом словарной функции, содержит все автоматы, сводимые к этой словарной функции.

 

В то же время, из незамкнутости z-множества словарной функции следует, что это множество нерегулярно, и для него не существует отвергающий автомат. Пример в Лемме о первой реакции в сериализации также показывает, что для существенно ненулевой словарной функции семейство автоматов, индуцируемое предикатом словарной функции, содержит автомат, несводимый к этой словарной функции. Иными словами, при тестировании нельзя ограничиться только конечными сериализациями, задаваемыми предикатом словарной функции. Заметим, что незамкнутость z-множества словарной функции существенно опирается на бесконечное число автоматов (и их z-множеств),═ реализующих эту словарную функцию. Здесь дело обстоит аналогично объединению бесконечного множества регулярных множеств конечных слов, которое может быть нерегулярным.

 

С другой стороны, для практических целей всегда можно ограничиться конечным семейством , рассматриваемых z-множеств. В качестве такого семейства можно взять семейство z-множеств автоматов из конечного семейства автоматов , например, автоматов, число состояний которых не превосходит некоторого N. Тогда ={Z[m]|mÎ }. В этом случае, как и следовало ожидать, z-множество словарной функции Z(W, )=È{ZÎ | W(Z)=W} становится не только замкнутым, но и регулярным, и, следовательно, для него существует отвергающий автомат. Мы докажем теорему аналогичную известной теореме о регулярности объединения конечного числа регулярных множеств конечных слов.

 

Теорема о реализации конечного семейства z-множества с данной словарной функцией: для каждого конечного семейства z-множеств ══и каждой автоматной словарной функции W существует автомат, z-множество которого совпадает с z-множеством Z(W, ).

 

Док-во: Для каждого z-множества из ═, словарная функция которого совпадает с заданной, то есть, для каждого элемента множества {ZÎ | W(Z)=W} выберем автомат, реализующий это z-множество. Требуемый автомат строится как объединение этих автоматов: возьмем копии всех этих автоматов, добавим новое начальное состояние v₀, и определим в нем пустые переходы во все копии начальных состояний этих автоматов. Поскольку множество ══конечно, получившийся автомат также будет конечным и его z-множество, очевидно, совпадает с объединением z-множеств копий автоматов, то есть, с Z(W, ). Теорема доказана.

 

Из этой теоремы непосредственно следует следующая

 

Теорема о предикате словарной функции для ограниченного семейства z-множеств (автоматов): Предикат словарной функции для ограниченного семейства z-множеств (автоматов) индуцирует семейство всех автоматов, сводимых к этой словарной функции.

 

4. Проблемы тестирования соответствия

4.1. Модель и реализация. Адаптивный алгоритм тестирования

Под тестированием в настоящей статье понимается то, что в литературе имеет названия тестирование соответствия (conformance testing или просто test generation), обнаружение ошибок (fault detection ) или машинная верификация (machine verification ). Модель является способом описания функциональных требований к реализации. Это означает, что реализации, имеющие одну функциональность, не различаются при вынесении вердикта тестирования. Иными словами, модель описывает класс реализаций, имеющих заданную моделью функциональность. Мы предполагаем, что реализация √ это реализационный (тестируемый) асинхронный автомат, представляющий собой ╚черный ящик╩, о поведении которого мы можем судить по реакциям (выходным словам), выдаваемым им в ответ на тестовые воздействия √ входные слова.

 

В первом приближении модель должна описывать словарную функцию реализационного автомата. Будем предполагать, что такое описание задано в виде модельного (спецификационного) автомата, а сам модельный автомат задан явно (например, своим графом состояний). Следует подчеркнуть, что целью тестирования в этом случае является не проверка совпадения модельного и реализационного автомата, а только проверка их эквивалентности, как совпадения реализуемых ими словарных функций. Итак, в первом приближении целью тестирования является проверка того, что тестируемый автомат R имеет словарную функцию W, заданную моделью: W[R]= W. Более детально:

╥        Гипотеза об эквивалентной допустимости: Dom(W[R])=Dom(W)

╥        Условие эквивалентной корректности: "wÎDom(W) W[R](w)=W(w)

 

Если эти условия выполнены, будем говорить об эквивалентности реализации и модели, реализацию будем называть эквивалентной модели. Гипотеза об эквивалентной допустимости является предусловием тестирования, поскольку она не может быть проверена в процессе тестирования, а тестируемым условием (условием, проверяемым тестом) является условие эквивалентной корректности.

 

Следует подчеркнуть, что наше понятие эквивалентности отличается от понятия эквивалентности в [4], где эквивалентность автоматов включает соответствие состояний. Если определить словарную функцию для каждого состояния, рассматриваемого как начальное, то эквивалентность в [4] означает совпадение словарных функций соответствующих состояний, в то время как мы требуем совпадения словарных функций только для начальных состояний. Дело в том, что само соответствие состояний реализации и модели предполагает выход за пределы строгой схемы ╚черного ящика╩. Этот выход может происходить по двум направлениям.

 

1. Гипотезы о реализации. Как правило, при тестировании мы накладываем на возможные реализации некоторые ограничения, которые не проверяются при тестировании, но являются его предусловием. К таким ограниченям относятся ограничения на размер (число состояний) автомата и гипотезы о той или иной степени детерминизма автомата. Введенная нами выше гипотеза об эквивалентной допустимости тоже относится к числу таких гипотез.

 

2. Дополнительная информация, получаемая в процессе тестирования. Строгая схема ╚черного ящика╩ предполагает, что единственная информация, которую мы получаем в процессе тестирования, это выходные слова, выдаваемые автоматом в ответ на подаваемые на него тестом входные слова. Считается, что выполнение автомата по данному входному слову мгновенно, то есть, мы не можем наблюдать выборку стимулов из входной очереди и появление реакций в выходной очереди в процессе выполнения автомата. Это легко объясняется тем, что для любого автомата можно построить другой автомат, который осуществляет предварительную буферизацию воспринимаемых стимулов и, тем самым, задерживает выдачу реакций. Разумеется, такой буфер является расширением состояния автомата и для конечного автомата должен иметь конечный размер, но, если нет ограничений на размер самого автомата, то нет ограничений и на размер этого буфера.

Конечно, на практике мы, как правило, имеем возможность в той или иной степени определять относительный порядок во времени воспринимаемых автоматом стимулов и получаемых реакций. Такая информация о сериализациях тестируемого автомата может говорить об ошибке в смысле реализуемой им словарной функции. Например, если для входного слова, начинающегося со стимулов x₀x₁, словарная функция определяет только такие выходные слова, которые начинаются с реакции y₁, а для x₀x₂ √ с y₂, то выдача автоматом реакции y₁ до приема второго стимула является ошибкой. С другой стороны, мы можем считать, что модель описывает не только словарную функцию, но и возможные сериализации, тем самым накладывая ограничения на реализацию этой словарной функции в тестируемом автомате. В этом случае функциональные требования к тестируемому автомату более жесткие, чем может быть задано самой словарной функцией.

Еще одним способом получить дополнительную информацию является наличие специальной операции чтения состояния (status message) тестируемого автомата. Здесь предполагается, что такая операция чтения дает достоверный результат, то есть, не входит в число стимулов, реакцию на которые нужно тестировать. Другим способом является наличие специальной операции сброса автомата в начальное состояние (reset), которая также должна быть достоверна. В этом случае мы имеем информацию о состоянии реализации, по крайней мере, сразу после выполнения такой операции сброса.

 

Тестом на соответствие обычно называют такое входное слово, что по любому полученному от тестируемого автомата выходному слову можно однозначно определить, эквивалентна реализация модели или нет. Это слово называют проверяющим словом (checking sequence). Если такое слово существует, то далее интересуются его длиной для ограниченного (числом состояний и/или переходов) автомата и сложностью алгоритма поиска такого входного слова. В общем виде проблема соответствия очень сложна и здесь мы рассмотрим лишь некоторые более частные проблемы, решение которых необходимо для решения проблемы соответствия .

 

Прежде всего, следует отметить, что входное слово может быть не только заранее заданным (preset sequence), но и вычисляемым в процессе тестирования на основе анализа получаемых реакций. Фактически,═ такое адаптивное входное слово (adaptive sequence) является алгоритмом тестирования, вычисляющим следующий стимул (или последовательность стимулов) в зависимости от полученных к этому моменту реакций.

 

Рассмотрим тестирование как протяженный во времени процесс подачи стимулов на автомат и получения от него реакций. Во-первых, мы предполагаем, что подаваемый на автомат стимул не ╚пропадает╩, то есть, если автомат принимает стимул, то он перед этим принял все предыдущие стимулы. Именно это описывается абстракцией входной очереди. Исключение составляют пустые стимулы, поскольку у нас может не быть возможности точной их реализации, то есть, мы не можем гарантировать, что между двумя непустыми воспринимаемыми стимулам автомат воспримет ровно столько пустых стимулов, сколько мы хотим. Эта проблема обсуждается ниже. Пока будем предполагать, что пустые стимулы реализованы точно. Во-вторых, мы предполагаем, что в процессе подачи на автомат стимулов мы имеем возможность получать выдаваемые автоматом реакции одну за другой так, что в каждый момент времени последовательность уже полученных реакций представляет собой начало выходного слова, выдаваемого автоматом.

 

Адаптивный алгоритм тестирования для словарной функции W можно представить себе в виде последовательности шагов. На каждом═ i-ом шаге на автомат подается некоторое квази-конечное входное слово w_ie^w,═ и в какой-то момент времени после подачи последнего непустого стимула мы обнаруживаем, что получили конечное выходное u_i. На первом шаге, слово w₁e^w должно быть допустимо и проверяется, что u₁ может быть началом возможного выходного слова, то есть, существует uÎW(w₁e^w) такое, что u₁£u. Второй шаг мы начинаем, когда имеется неопределенность в числе концевых пустых стимулов первого входного слова, то есть, когда реально на автомат подано некоторое конечное входное слово вида w_ie^*. Предполагается, что допустимо любое входное слово вида w₁e^*w₂e^w, и проверяется, что, по крайней мере, для некоторых из них u₁u₂ может быть началом возможного выходного слова. В целом, если тестирование завершается после k-го шага, то должно быть допустимо любое входное слово вида u₁e^*u₂e^*…u_ie^*…u_ke^w, и проверяется, что, по крайней мере, для некоторых из них слово u₁u₂…u_i…u_k является началом возможного выходного слова.

 

Сначала рассмотрим две проблемы избыточности: проблема избыточности реализации (реализационного входного домена) и проблема избыточности модели (модельной словарной функции).

4.2. Проблема избыточности реализации

Проблема избыточности реализации (реализационного домена): Реализация, делающая все то, что она должна делать в соответствии с функциональностью, заданной моделью, может допускать входные воздействия, не описываемые моделью. Как правило, при тестировании не ставится задача проверки того, что делает реализация для этих немоделируемых тестовых воздействий. В терминах автомата и его словарной функции это означает: при тестировании мы подаем на тестируемый автомат только те входные слова, которые допустимы в модели, хотя реализация может допускать и другие входные слова.

 

Будем говорить, что реализационный автомат R частично эквивалентен модельной словарной функции W, если выполнены следующие два условия:

╥        Гипотеза о частичной допустимости: Dom(W[R])ÊDom(W)

╥        Условие эквивалентной корректности: "wÎDom(W) W[R](w)=W(w)

Гипотеза о частичной допустимости является предусловием тестирования, поскольку она не может быть проверена в процессе тестирования, а тестируемым условием═ является условие эквивалентной корректности. В дальнейшем, по умолчанию, под "гипотезой о допустимости" мы будем понимать именно "гипотезу о частичной допустимости". Заметим, что наше понятие частичной эквивалентности аналогично понятию квази-эквивалентности в [3].

4.3. Проблема избыточности модели

Проблема избыточности модели (модельной словарной функции): Модель описывает множество возможных поведений реализации при заданном допустимом воздействии на нее. В терминах автомата и его словарной функции это означает, что значение словарной функции на данном входном слове является множеством выходных слов. Если это множество состоит более, чем из одного выходного слова, это означает, что модель разрешает реализации выдавать любое из этих выходных слов. Однако, мы не можем требовать, чтобы реализация для каждого возможного выходного слова имела выполнение, выдающее это слово. Во-первых, это невозможно проверить, если единственный способ воздействия на реализацию √═ ввод входного слова. Если для данного входного слова возможных выходных слов несколько, то выбор того или иного выходного слова в автомате, по определению, недетерминирован. Эта проблема обсуждается в следующем разделе. Во-вторых, функциональность обычно понимается как раз в том смысле, что реализация может выдавать любое из возможных выходных слов. Это означает, что значение словарной функции реализационного автомата на данном допустимом входном слове должно быть вложено в значение модельной словарной функции на этом же входном слове, но не обязано совпадать с ним.

 

Будем говорить, что реализационный автомат R сводим к модельной словарной функции W, если выполнены следующие два условия:

╥        Гипотеза о частичной допустимости: Dom(W[R])ÊDom(W)

╥        Условие частичной корректности: "wÎDom(W) W[R](w)ÍW(w)

 

Тестируемым условием═ является условие частичной корректности. В дальнейшем, по умолчанию, под "условием корректности" мы будем понимать именно "условие частичной корректности".

4.4. Проблема недетерминизма

Проблема недетерминизма словарной функции. Как было сказано выше, условие корректности в полном объеме невозможно проверить. Если для данного входного слова возможных выходных слов несколько, то выбор того или иного выходного слова в автомате, по определению, недетерминирован. Поэтому сколько бы раз мы не подавали на тестируемый автомат данное допустимое входное слово и получали возможное (соответствующее модели) выходное слово, у нас не может быть гарантии, что при следующей попытке будет выдано также возможное выходное слово.

 

Поэтому предполагается выполненной следующая

╥        Гипотеза об однородности недетерминизма: Если автомат для допустимого входного слова выдает возможное выходное слово, то он это делает всегда, то есть, значение словарной функции автомата на этом входном слове состоит только из возможных слов:
"wÎDom(W) $uÎW[R](w)ÇW(w) Þ W[R](w)ÍW(w).

 

Если гипотезы о допустимости и однородности недетерминизма верны, то для проверки сводимости реализации к модели достаточно проверить следующее тестируемое

╥        Условие однократной корректности: "wÎDom(W) первое же выданное реализацией выходное слово uÎ W(w).

 

4.5. Проблема бесконечности модельного домена

Проблема бесконечности модельного домена. Домен модельной словарной функции, вообще говоря, является бесконечным и поэтому проверка тестируемого условия "в лоб", то есть, для каждого слова из домена, не может быть выполнена за конечное время.

 

Чтобы обойти эту проблему, определяют покрытие домена - конечное множество подмножеств домена CoverageÍ2^Dom(W) такое, что ÈCoverage=Dom(W). Элементы покрытия называются областями. При этом предполагается выполненной следующая

╥        Гипотеза об однородности покрытия: для каждой области покрытия, если тестируемое условие выполнено для некоторого элемента области, то оно выполнено для всех элементов области: "CÎCoverage ($wÎC═ W[R](w)ÍW(w)) Þ "w`ÎC W[R](w`)ÍW(w`).

 

Если гипотезы о допустимости и однородности покрытия верны, то для проверки сводимости реализации к модели достаточно проверить следующее тестируемое

╥        Условие выборочной корректности: "CÎCoverage для первого подаваемого на реализацию входного слова wÎC W[R](w)ÍW(w).

 

Если задано покрытие Coverage и верны гипотезы о допустимости, однородности недетерминизма и однородности покрытия, то для проверки сводимости реализации к модели достаточно проверить следующее тестируемое условие:

╥        Условие выборочной однократной корректности: "CÎCoverage для первого подаваемого на реализацию входного слова wÎC выданное реализацией выходное слово uÎ W(w).

 

4.6. Итерация входных слов

Тестирование есть последовательность шагов тестирования, на каждом из которых осуществляется подача на тестируемый автомат входного слова w, получение выходного слова u и проверка того, что uÎW(w). Здесь возникает проблема перебора входных слов, подаваемых тестом на шагах тестирования. Если задано покрытие Coverage и верна гипотеза об однородности покрытия, достаточно перебрать хотя бы по одному входному слову из каждой области покрытия.

Для этого определяют конечное итерируемое множествоIterateÍDom(W), содержащее, по крайней мере, по одному элементу из каждой области покрытия, то есть, {CÎCoverage|CoverageÇIterate¹Æ}=Coverage. Итерация входных слов осуществляется как перебор элементов итерируемого множества.

 

Итерируемое множество на практике удобнее задавать избыточным в том смысле, что его собственное подмножество также является итерируемым множеством для данного покрытия. Эту избыточность можно уменьшить, используя фильтрацию. Пусть:

╥        итерируемое множество упорядочено (перенумеровано) Iterate={w[i]|i=1..n};

╥        покрытие также упорядочено (перенумеровано) Coverage={C[j]|j=1..m};

╥        для каждой области C[j]ÎCoverage определен предикат на итерируемом множестве P[j] º wÎC[j].

 

Введем массив булевских переменных B длиной m, инициализированных false. Отфильтрованная последовательность входных слов FilterIterate вычисляется следующим образом. Итерируя множество Iterate, для каждого входного слова w из Iterate перебираем все области покрытия C[j], для которых B[j] равно false, и с помощью предиката P[j] определяем, принадлежит ли w соответствующей области. Для каждой перебираемой области C[j], если wÎC[j], то устанавливаем B[j]:=true. Если это произошло хотя бы один раз (w принадлежит хотя бы одной перебираемой области), то помещаем w в отфильтрованную последовательность FilterIterate.

4.7. Проблема бесконечных входных слов

По существу, эту проблему мы изучали в части 3. Хотя словарная функция определяется на бесконечных входных словах, поскольку это удобная математическая абстракция, однако, при тестировании приходится иметь дело только с конечными словами. Конечное входное слово можно понимать как бесконечное слово, в котором имеется только конечное число непустых стимулов; такие бесконечные слова мы назвали квази-конечными. Пустые стимулы, расположенные во входном слове до последнего непустого стимула моделируют ╚паузы╩ между последовательными непустыми стимулами, а бесконечная последовательность пустых стимулов после последнего непустого стимула √ конец слова, то есть, завершение подачи стимулов на автомат в данном тестовом эксперименте.

 

Мы выяснили, что словарная функция автомата, вообще говоря, не восстанавливается однозначно по своему квази-конечному сужению. В этой ситуации можно 1) ограничиться такими классами автоматов, для которых словарная функция однозначно определяется ее квази-конечным сужением, или 2) такими функциональными требованиями к автомату, которые могут быть сформулированы в терминах квази-конечного сужения словарной функции, то есть, проверять поведение автомата только на квази-конечных входных словах и, если на таких словах оно правильно, то делать вывод, что реализация соответствует модели. В этих случаях мы как бы не обращаем внимание на поведение автомата на ╚настоящих╩, содержащих бесконечное число непустых стимулов, входных словах.

 

В то же время, поведение автомата на таких ╚настоящих╩ входных словах может оказаться существенным с точки зрения функциональных требований к автомату. Обычно программные или аппаратные системы прекращают выдачу реакций, если в течении длительного времени на них не поступают (непустые) стимулы, но существуют системы с ╚инвертированным╩ поведением, которые, наоборот, не выдают реакций, если стимулы периодически поступают, а при длительном их отсутствии начинают выдавать ╚аварийные╩ реакции, сигнализирующие об обрыве потока стимулов.

 

В этом случае можно попробовать использование некоторого предиката на конечных сериализациях и информации о сериализациях, возникающих при работе автомата для тестовых воздействий. Мы показали, что, если функциональные требования настолько жесткие, что описывают не только словарную функцию, но и множество вполне-допустимых сериализаций автомата, то такой предикат можно использовать для проверки получаемых при тестировании сериализаций. Однако, если предикат описывает, фактически, саму словарную функцию, то есть, допускает все сериализации, которые могут возникнуть при работе любого автомата с данной словарной функцией, то в общем случае такой предикат не сможет отвергнуть поведение некоторых автоматов с другой словарной функцией. В то же время, если ограничиться конечным семейством автоматов (например, автоматами с ограниченным числом состояний), то проблема может быть решена.

 

Если у нас не задана словарная функция, а только предикат p конечных сериализаций (неважно, что это может быть, например, предикат некоторой словарной функции или предикат z-множества, определяющего словарную функцию), то тестирование производится на основе этого предиката следующим образом:

╥        в качестве конечного входного слова w_t выбираются x-подслово xz конечной сериализации z допускаемой предикатом: zÎU(p) w_t=xz;

╥        для полученной в тестовом эксперименте конечной сериализации z_t (xz_t=w_t) проверяется, что она допускается предикатом: z_tÎU(p).

 

Если же у нас задана как словарная функция W, так и предикат p конечных сериализаций, то последний рассматривается как дополнение к словарной функции, то есть, используется только для уточнения сериализации пары (входное слово, выходное слово), удовлетворяющей словарной функции. Более детально тестовый эксперимент строится по следующей схеме:

╥        в качестве конечного входного слова w_t выбирается начальный отрезок входного слова w из домена словарной функции: wÎDom(W) w_t<w;

╥        из полученной в тестовом эксперименте конечной сериализации z_t (xz_t=w_t) выбирается конечное выходное слово - y-подслово yz_t и проверяется, что оно удовлетворяет словарной функции: $w`ÎDom(W) $uÎW(w`) w_t<w` yz_t<u; если это не так, фиксируется ошибка;

╥        проверяется, описывает ли предикат сериализации для пары (w_t,yz_t): $zÎU(p) xz=w_t yz=yz_t; если нет, то считаем, что предикат не запрещает любую сериализацию такой пары и тестовый эксперимент заканчивается успешно;

╥        если предикат описывает некоторые сериализации для пары (w_t,yz_t), то проверяем, что полученная сериализация z_t является одной из них: z_tÎU(p); если это не так, то фиксируется ошибка.

 

Разумеется, для использования метода предиката у нас должна быть какая-то возможность получать информацию не только о выходных словах, но и о сериализациях. На практике, мы во многих случаях можем такую информацию получить. Один из способов следующий. Пусть временем срабатывания автомата по пустому переходу можно пренебречь, а время срабатывания по приему стимула ограничено снизу числом t_min и сверху число t_max. Тогда, если первая реакция, поступает через время nt_max£t£mt_min от начала тестирования, то мы можем утверждать, что она располагается в сериализации не раньше n-го и не позже m-го стимула. Например, при t_min=2, t_max=4 и t=9 первая реакция имеет в сериализации индекс от 2 до 5, так как 2*4<9<5*2.

 

В то же время, этот пример показывает, что при тестировании у нас может не быть возможности точно определить сериализацию входного и выходного слова. Фактически, мы можем определить множество возможных сериализаций. В целом, если в результате тестового эксперимента получена не одна сериализация, а множество Z_t возможных конечных сериализаций, то описанные выше проверки результатов тестового эксперимента проводятся для каждой сериализации множества z_tÎZ_t. Если хотя бы одна сериализация выдерживает проверку, то прекращаем проверку непроверенных сериализаций и считаем, что автомат вел себя правильно ("презумпция невиновности"). Если ни одна сериализация не выдерживает проверку, фиксируем ошибку.

 

Заметим, что разные сериализации определяют, вообще говоря, разные постсостояния (множества постсостояний) автомата. Поэтому, если нам нужно знать постсостояние (для того, чтобы давать следующее входное слово не в начальном состоянии, а в постсостоянии), то имеет смысл проверять каждую сериализации из множества Z_t возможных сериализаций (а не до первой выдерживающей проверку). Те сериализации, которые выдержали проверку, определяют множество z-раскрасок маршрутов, по которым мог пройти автомат и, тем самым, множество возможных постсостояний (концов этих маршрутов). Подробнее эту проблему рассмотрим ниже.

 

Множество возможных сериализаций при тестировании может быть задано наиболее естественным способом как частичный порядок на вхождениях стимулов и реакций во входное и выходное слова. Входное слово определяет линейный порядок стимулов, а выходное слово - линейный порядок реакций. Дополнительный частичный порядок, таким образом, связывает стимулы и реакции. В рассмотренном выше примере первая реакция находится не раньше 2-го и не позже 5-го стимула. Этот дополнительный частичный порядок индуцирует множество Z_t линейных порядков, не противоречащих ему.

4.8. Проблема пустых стимулов

Пустой стимул является абстракцией, моделирующей пустоту входной очереди в момент ее опроса автоматом═ в рецептивном состоянии. Теперь возникает проблема реализации этой абстракции, то есть, реализации пустого стимула. Понятно, что реализовать бесконечную последовательность пустых стимулов после последнего непустого стимул легко: надо просто перестать подавать стимулы на автомат. Труднее реализовать неконечные пустые стимулы, моделирующие ╚паузы╩ различной длительности (измеряемой в числе пройденных рецептивных состояний) между последовательными непустыми стимулами.

4.8.1. Перехват операции receive

Простейший способ реализации пустого стимула основан на перехвате тестовой системой обращения автомата к входной очереди в рецептивном состоянии. Будем считать, что такое обращение реализуется операцией receive, возвращающей головной стимул, если очередь не пуста, или сообщающей об отсутствии стимула, если очередь пуста. Заметим, что асинхронный автомат отличается от классического автомата Мили, в частности, тем, что для последнего используется receive с ожиданием и поэтому автомату не сообщается об отсутствии стимула. Если по операции receive автомат попадает в тест, то сам тест возвращает очередной стимул входного слова, если этот стимул непуст, или сообщает о пустоте очереди, если этот стимул пуст.

 

Недостатком этого способа является то, что подобной возможности перехвата операции receive может не быть. В этом случае возможны три варианта: 1) ограничиться такими автоматами, поведение которых не зависит от наличия или отсутствия пустых стимулов во входном слове; 2) ограничиться такими входными словами, которые можно реализовать; 3) применять "нечеткие" входные слова, в которых число пустых стимулов в нужных местах может быть определено лишь с некоторой степенью точности и, соответственно, ограничиться такими автоматами, в которых любое из точных слов, соответствующих нечеткому входному слову, допустимо.

4.8.2. Серийное тестирование без пауз и стационарное тестирование

Среди допустимых квази-конечных входных слов есть два крайних подмножества слов, которые могут быть реализованы при некоторых предположениях:

1.      Квази-конечные входные слова без пустых стимулов, точнее, слова, в которых все пустые стимулы располагаются после последнего непустого стимула. Множество таких слов X^*^{e^w}.

2.      Квази-конечные входные слова, в которых между любыми последовательными непустыми стимулами располагается достаточно большое число пустых стимулов.

 

Подмножество 1 может быть реализовано в предположении, что тест успевает подать на автомат следующий непустой стимул до того, как автомат захочет его прочитать. Такое тестирование будем называть серийным тестированием без пауз. Если тест и автомат реализованы процессами на одном процессоре, то достаточно, чтобы процесс теста имел больший приоритет, чем процесс автомата. В этом случае тест поместит во входную очередь все непустые стимулы и только после этого начнет работать процесс автомата. Если же тест и автомат реализованы процессами на разных процессорах, то, по-видимому, нужно, чтобы процессор теста был достаточно быстрый по сравнению с процессором автомата: цикл теста по посылке одного непустого стимула должен выполняться быстрее, чем переход автомата, ограниченный сверху максимальным временем срабатывания t.

 

Есть и другой способ реализации подмножества 1. Для этого достаточно, чтобы работа автомата начиналась с его начального состояния после того, как тест поместил во входную очередь все непустые стимулы входного слова. Иными словами, предполагается, что автомат начинает свою работу с начального состояния по специальному стартовому сигналу, который тест подает после помещения во входную очередь всех непустых стимулов.

 

Подмножество 2 имеет смысл для автоматов класса A5, в которых любое квази-конечное слово переводит автомат в терминальное состояние или принимающее состояние без e-переходов в другие состояния (есть только e- петля); такие состояния будем называть стационарными. Такой автомат класса A3 √ это, очевидно, автомат, в котором каждый циклический маршрут, кроме e-петель, содержит x-переходы, то есть, прием стимулов. В стационарном состоянии автомат либо останавливается, либо ожидает поступления непустого стимула. В этом случае следующий непустой стимул подается на автомат после его перехода в стационарное нетерминальное состояние. Такое тестирование будем называть стационарным.

 

Какое время тест должен выждать прежде, чем подать следующий непустой стимул? Очевидно, это время ограничено сверху максимальным временем перехода автомата по предыдущему непустому стимулу плюс время прохождения в стационарное состояние по маршруту, содержащему только пустые, посылающие и e-переходы. Поскольку нет циклов из таких переходов, кроме e-петель, максимальная длина такого пути равна n-1, где n - число состояний автомата. Следовательно, тайм-аут между последовательными непустыми стимулами можно установить равным t+(n-1)t=nt, где t - максимальное время срабатывания автомата.

4.8.2. Автоматы с однородным поведением

Можно не беспокоиться о реализации пустых стимулов, если тестируемый автомат обладает следующим свойством.

 

Однородное поведение: Если словарная функция W автомата определена на слове w, то она определена также на любом слове w`, полученном из w удалением и/или добавлением в произвольные места произвольного конечного числа пустых стимулов, и принимает на нем то же значение W(w`)=W(w).

 

Автоматы, обладающие этим свойством будем называть автоматами с однородным поведением, а класс таких автоматов обозначим A6. Мы уже изучали подкласс A6 - класс A0 - автоматы без смешанных состояний и e-переходов. Если привести эти автоматы к классу A3, то отсутствие e-переходов превращается в отсутствие e-переходов, не являющихся петлями. Иными словами, автоматы класса A0 - это автоматы без смешанных состояний, в которых все e-переходы - это петли в принимающих состояниях.

 

Вместе с тем, свойство независимости словарной функции от вставки и удаления пустых стимулов не является характеристическим для класса A0, то есть, класс автоматов, обладающих этим свойством, не совпадает с классом A0: A0ÌA6. Пример приведен на рис.4.8.1; в этом автомате нарушается свойство 3 автомата класса A0: слово x₁e^w допустимо, слово x₁x₁e^w недопустимо, однако, W(x₁e^w)={(y^w)} не содержит конечного выходного слова.

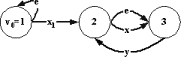
Рис.4.8.1

 

Здесь представляют интерес следующие две пока не решенные задачи:

1.      Описать класс автоматов с однородным поведением A6.

2.      Рассмотреть подкласс A6`ÌA6, в котором для всех квази-конечных входных слов выходные слова конечны. Есть гипотеза, что этот подкласс является также подклассом A0: A6`ÌA0ÌA6.

 

При тестировании автоматов класса A6 мы имеем непроверяемую во время тестирования гипотезу об однородном поведении, и подаем квази-конечные слова с теми пустыми паузами между непустыми стимулами, которые получатся. Отдельный интересе представляет тестирование с═ варьированием длительность этих пауз, разумеется без гарантии (и не ставя такую цель) перебрать все возможные длительности.

4.8.4.═ Автоматы с однородной допустимостью

Требование к автомату, определяющее класс A6 автоматов с однородным поведением, может быть ослаблено:

 

Однородная допустимость: Если словарная функция W автомата определена на слове w, то она определена также на любом слове w`, полученном из w удалением и/или добавлением в произвольные места произвольного конечного числа пустых стимулов.

 

Автоматы, обладающие этим свойством, будем называть автоматами с однородной допустимостью, а класс таких автоматов обозначим A7ÉA6. Иными словами, для автоматов с однородной допустимостью A7, в отличии от автоматов с однородным поведением A6, не требуется, чтобы , словарная функция на входных словах w и w`, отличающихся только наличием или отсутствием конечного числа пустых стимулов, принимала одно и то же значение W(w`)=W(w), а только одинаковая допустимость этих слов.

 

Тестирование таких автоматов основано на предположении, что при попытке подать на автомат допустимое входное слово w, выдавая стимул за стимулом и делая ╚паузы╩ для пустых стимулов, реально автомат может получить не слово w, а слово w`, которое, тем не менее, также допустимо. Поскольку не известно, какое именно входное слово получил автомат, при получении выходного слова u мы проверяем по словарной функции все пары слов (w`,u), где w` отличается от w конечным числом пустых стимулов. Если хотя бы одна такая пара удовлетворяет словарной функции, то, по "презумпции невиновности", считаем, что автомат выполнялся правильно.

 

В определении свойства однородной допустимости говорилось о добавлении или удалении конечного числа пустых стимулов. Покажем, что это ограничение можно снять: 1) разрешается удалять бесконечное число пустых стимулов, но так, чтобы слово оставалось бесконечным; 2) разрешается вставлять бесконечное число стимулов, причем, если бесконечное число стимулов вставляется в одно место, то последующие стимулы исчезают. Вообще, для квази-конечных слов снятие ограничения ничего не дает, однако, для ╚настоящих╩ бесконечных слов это существенно; в частности вставкой бесконечного числа пустых стимулов после некоторого непустого стимула мы превращаем его в квази-конечное слово.

 

Доказательство будем вести от противного. Пусть в автомате с однородной допустимостью слово w допустимо, а слово w`, полученное из него вставкой или удалением произвольного числа пустых стимулов, недопустимо. Тогда при некотором выполнении автомата по входному слову w` фиксируется ошибка неспецифицированного ввода. В этот момент, очевидно, автомат прочитал из входной очереди начальный отрезок входного слова конечной длины w`[1..n], который соответствует некоторому отрезку w[1..m], то есть, получен из него вставкой и/или удалением конечного числа пустых стимулов. Но тогда это выполнение возможно также для входного слова w``=w`[1..n]^w[m+1..], которое отличается от w конечным числом пустых стимулов, то есть, слово w`` недопустимо, что противоречит свойству однородной допустимости.

 

Для словарной функции с однородной допустимостью W можно определить производную словарную функциюE(W) как объединение значений W на всех бесконечных словах, отличающихся от данного добавлением или удалением любого числа пустых стимулов:

╥        Dom(E(W))=Dom(W)

╥        "wÎDom(E(W)) E(W)(w)=È{ W (w`)|w`ÎE(w)} - здесь E(w) - множество бесконечных слов, получаемых из w добавлением и/или удалением любого числа пустых стимулов.

 

Фактически, при тестировании мы будем проверять, что тестируемый автомат сводим не к исходной, а к производной словарной функции. Производная словарная функция E(W), очевидно, уже является однородной по поведению.

 

Как по автомату с однородной допустимостью класса A3, реализующему словарную функцию W, построить автомат, реализующий производную словарную функцию E(W)? Это можно сделать следующей процедурой (рис.4.8.2):

1.      Вставка пустых стимулов. Добавим до и после каждого принимающего перехода по непустому стимулу (v,x,v`) произвольное число e-переходов: добавляем три новых состояния v<sub>1</sub>, v<sub>2</sub>, и v<sub>3</sub>, определяем в них e-петли (v<sub>i</sub>,e,v<sub>i</sub>), i=1,2,3, в состоянии v определяем x-переход (v,x,v<sub>1</sub>) и e-переходы (v,e,v<sub>2</sub>) и (v,e,v<sub>3</sub>), в состоянии v<sub>1</sub> определяем e-переход (v<sub>1</sub>,e,v`), в состоянии v₂ определяем x-переход (v₂,e,v`), а в состоянии v₃ определяем x-переход (v₂,e,v₁).

2.      Удаление пустых стимулов. Для каждого e-перехода (v,e,v`), где v¹v`, сдублируем каждый переход в состояние v на переход в состояние v`: для e-перехода (v<sub>e</sub>,e,v) добавим переход (v<sub>e</sub>,e,v`), для x-перехода (v_x,x,v) добавим переход (v_x,x,v`), для y-перехода (v<sub>y</sub>,y,v) добавим переход (v<sub>y</sub>,y,v`).

Рис.4.8.2

 

На домене однородной по поведению словарной функции можно определить отношение эквивалентности EÍDom(E(W))²: (w,w`)ÎE, если w`ÎE(w). Однородность по поведению как раз и означает, что словарная функция принимает одинаковые значения на эквивалентных входных словах. После этого можно определить словарную фактор-функциюF(W):

╥        Dom(F(W))=E(Dom(W)), где E(Dom(W)) - множество классов эквивалентности E

╥        "WÎDom(F(W)) F(W)(W)=E(w), где wÎW

 

Каноническим входным словом будем называть такое входное слово, в котором за пустым стимулом, если он есть, следуют только пустые стимулы. Множество канонических входных слов - это (X^*^{e^w})ÈX^w, где X^*^{e^w} - множество канонических квази-конечных слов, а X^w - множество остальных канонических слов - бесконечных слов без пустых стимулов. Нас будет интересовать не столько фактор-функция, сколько каноническая словарная функцияC(W), определенная на канонических представителях классов эквивалентности допустимых слов:

╥        Dom(C(W)) = ((X^*^{e^w})ÈX^w) Ç Dom(W)

╥        "wÎDom(C(W)) C(W)(w)=E(w)

 

Фактически, при тестировании мы будем проверять, что тестируемый автомат сводим к канонической словарной функции. Более точно: мы будем подавать на автомат канонические входные слова, автомат при этом будет получать возможно другое входное слово, но из того же класса эквивалентности, а выходное слово мы будем проверять по канонической словарной функции. При этом мы будем предполагать, что выполнены непроверяемые при тестировании

╥        Гипотеза об однородной допустимости: Словарная функция тестируемого автомата является однородно допустимой.

╥        Гипотеза об однородной корректности: Если автомат правильно себя ведет на некотором входном слове, то он правильно себя ведет на всем классе эквивалентности (по вставке и/или удалению пустых стимулов) этого входного слова.

 

Эти гипотезы, тем самым, предполагают некоторое предопределенное покрытие домена, а именно - разбиение на классы эквивалентности E. Всякое дополнительное покрытие будет, фактически, покрытием фактор-домена, то есть, множества классов эквивалентности E. Представляет интерес представление в модели канонической словарной функции.

 

Как по автомату с однородной допустимостью класса A3, реализующему производную словарную функцию E(W), построить автомат, реализующий каноническую словарную функцию C(W)? Это можно сделать следующей процедурой:

1.      Скопировать автомат и в копии удалить все x-переходы (принимающие переходы по непустым стимулам). Копию состояния v будем снабжать индексом - v^c.

2.      Каждый e-переход (v,e,v`) заменим на e-переход (v,e,v`^c), определенный в том же состоянии-оригинале v, но ведущий в постсостояние-копию v`^c.

 

Иными словами, первый же═ e-переход переводит нас в автомат-копию, где далее мы совершаем только пустые, посылающие и e-переходы.

 

Поскольку тестирование мы проводим только на квази-конечных словах, все предыдущие рассуждения, вообще говоря, следовало бы скорректировать с учетом этого. В частности, эквивалентными квази-конечному слову считать только квази-конечные слова и соответствующим образом определять производную, фактор- и каноническую словарные функции.

4.9. Проблема выходных слов

Следующая проблема тестирования - это проблема выходных слов, распадающаяся на две проблемы: 1) Сколько времени мы должны ожидать получения очередной реакции? 2) Сколько времени мы должны получать и проверять реакции, чтобы убедиться, что полученное конечное выходное слово достаточно ╚репрезентативно╩, то есть, является возможным выходным словом или достаточно большим начальным отрезком возможного бесконечного выходного слова?

4.9.1. Тайм-аут на ожидание очередной реакции

Тайм-аут на ожидание реакции не следует понимать так, что, если в течении этого времени реакция не поступила, то она никогда не поступит. При наличии циклов по пустым и e-переходам, в которые мы можем попасть после выборки из входной очереди всех непустых стимулов квази-конечного входного слова, а также при наличии циклов по пустым переходам еще до выборки последнего непустого стимула, очередная реакция может быть выдана после прохождения любого числа раз по таким циклам. Однако, в этом случае существует и такое выполнение, когда автомат не выходит из такого цикла, бесконечно двигаясь по нему и не выдавая реакций. Поэтому тайм-аут предлагается понимать так, что, если за это время не поступила очередная реакция, то возможно такое выполнение, при котором она и не поступит. Если такое выполнение удовлетворяет словарной функции, то можно не ожидать реакции сверх тайм-аута, поскольку это ожидание может продолжиться бесконечно. С другой стороны, если очередная реакция, согласно словарной функции, должна поступить обязательно, то тайм-аут должен быть больше времени максимального времени ожидания такой обязательной реакции.

 

Определим формально понятие обязательной реакции. Будем говорить, что для входного квази-конечного слова w и выходного слова uÎW(w) i-ая реакция, где i£nu, обязательна, если слово u[1..i-1]ÏW(w).

 

Определение тайм-аута тесно связано со следующими ограничениями:

╥        Максимальное время срабатывания автомата - t. Если бы такого ограничения не было, то, очевидно, не было бы ограничения и на время ожидания очередной обязательной реакции.

╥        Ограничение на размер автомата, точнее, число состояний автомата ограничено сверху числом n. Действительно, если такого ограничения нет, то перед любым переходом посылающим обязательную реакцию можно было бы вставить цепочку из любого конечного числа пустых переходов с ненулевым временем срабатывания и, тем самым, в полученном автомате превысить любое наперед заданное время ожидания обязательной реакции.

 

Будем считать, что автомат приведен к классу A2. Обозначим число принимающих состояний n_s и число посылающих состояний n_r. n=n_s+n_r. Обозначим через s число стимулов во входном квази-конечном слове w до последнего непустого стимула включительно.

 

Теорема о времени ожидания обязательной реакции: Время ожидания обязательной реакции не превосходит ((s+1)n_r+n_s)t.

 

Док-во: Пусть P - один из маршрутов выполнения для допустимого входного слова w. Обозначим через P_i отрезок P между i-1-ым и i-ым посылающим переходами, то есть, для некоторых индексов a и b P_i=P[a..b], P[a-1] - i-1-ый посылающий переход (при i=1 a=1) и P[b+1] - i-ый посылающий переход. Считая, что i-ая реакция может быть послана в конце прохождения i-ого посылающего перехода, нам следует показать, что, если i-ая реакция обязательна, то максимальная длина отрезка P_i (доi-ого посылающего перехода) не превосходит (s+1)n_r+n_s-1. Рассмотрим три случая:

 

1) Последний непустой стимул принимается автоматом до отрезка P_i, то есть, начальный отрезок P[1..a-1] содержит s принимающих переходов. В частности, это имеет место при s=0, то есть, w=e^w. Очевидно, P_i содержит только пустые и e-переходы. Поскольку i-ая реакция обязательна, P_i не должен содержать цикла из пустых и e-переходов. Следовательно, его длина не превосходит n-1=n_r+n_s-1.

 

2) Последний непустой стимул принимается автоматом после отрезка P_i, то есть, начальный отрезок P[1..b] содержит меньше, чем s, принимающих переходов. В этом случае, P_i содержит пустые и принимающие переходы. Поскольку i-ая реакция обязательна, P_i не должен содержать цикла из пустых переходов. Такой цикл мог бы находиться только между двумя последовательными принимающими переходами, значит, между ними не может быть больше чем n_r-1 переходов. Число принимающих переходов в P_i не превосходит s-1. Учитывая пустые переходы до первого принимающего перехода в P_i и пустые переходы после последнего принимающего перехода в P_i, получаем, что число пустых переходов в P_i не превосходит s(n_r-1). Общая длина P_i не превосходит (s-1)+s(n_r-1)=sn_r-1.

 

3) Последний непустой стимул принимается автоматом внутри отрезка P_i. В этом случае, P_i содержит пустые и принимающие переходы. Поскольку i-ая реакция обязательна, P_i не должен содержать цикла из пустых переходов и, после приема последнего непустого стимула, - цикла из пустых и e-переходов. Цикл из пустых переходов мог бы находиться только между двумя последовательными принимающими переходами, значит, между ними не может быть больше чем n_r-1 дуг. Число принимающих переходов в P_i не превосходит s. Учитывая пустые переходы до первого принимающего перехода в P_i, получаем, что до приема последнего непустого стимула P_i содержит число пустых переходов не превосходящее s(n_r-1), а всего переходов до приема последнего непустого стимула включительно не более s+s(n_r-1)=sn_r. После приема последнего непустого стимула P_i содержит только пустые и e-переходы, число которых не может превосходить n-1=n_r+n_s-1. Следовательно, общая длина P_i не превосходит
sn_r+n_r+n_s-1=(s+1)n_r+n_s-1.

 

Для случая 1), поскольку s³0, имеем n_r+n_s-1£(s+1)n_r+n_s-1. Для случая 2, поскольку s³0 и n_s³0, имеем sn_r-1£(s+1)n_r-1£(s+1)n_r+n_s-1.

 

Теорема о времени ожидания обязательной реакции доказана.

 

Пример на рис.4.9.1 дает оценку снизу ((s+1)n_r+1)t для времени ожидания первой реакции, что совпадает с верхней оценкой при n_s=1.

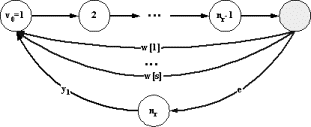
Рис.4.9.1

 

Для необязательной реакции время ее ожидания, естественно, может быть сколь угодно большим (бесконечным для выполнения без выдачи реакции). С другой стороны, полученная нами оценка дает также максимальное время ожидания необязательной реакции при условии, что она будет выдана и маршрут выполнения не проходит по циклам из пустых переходов и, после приема последнего непустого стимула, по циклам из пустых и e-переходов. Однократный проход по циклу пустых переходов занимает время не большее n_rt. Однократный проход по циклу пустых и e-переходов занимает время не большее (n_r+n_s) t=nt>n_rt. Таким образом, время ожидания необязательной реакции при условии, что маршрут выполнения проходит не более k раз по циклам пустых и e-переходов, не превосходит ((s+1)n_r+n_s)t+knt. Задавая число k, мы, тем самым, можем тестировать автомат при всех выполнениях, при которых проходятся не более k раз циклы пустых и e-переходов. Для остальных выполнений у нас должна быть сформулирована

╥        гипотеза о необязательных реакциях: если автомат правильно себя ведет при числе проходов по циклам пустых и e-переходов не превосходящем k, то и при остальных выполнениях он также ведет себя правильно.

4.9.2. Время ожидания репрезентативного выходного слова

Согласно словарной функции W выходное слово u возможное для входного слова w может оказаться бесконечным. Естественно, при тестировании мы не можем ждать бесконечное время, чтобы получить это бесконечное выходное слово. В таком случае нам хотелось бы гарантированно получить хотя бы те реакции, которые выдаются до того, как автомат выбрал последний непустой стимул, плюс еще те реакции, которые он может выдать после этого до попадания в цикл по посылающим, пустым и e-переходам (после приема последнего непустого стимула во входном слове остаются только пустые стимулы). Иными словами, мы хотим, чтобы автомат прошел начальный отрезок маршрута выполнения, содержащий прием всех непустых стимулов (или всех тех непустых стимулов, после приема которых он вообще перестает выбирать стимулы из входной очереди) и после этого содержащий цикл по посылающим, пустым и e-переходам. Естественно, что, если на таком отрезке маршрута имеются циклы по пустым переходам, то время ожидания последующей реакции может быть сколь угодно большим. Но в этом случае такая реакция необязательна и мы ее можем никогда не получить.

 

До приема последнего непустого стимула включительно, при условии, что не встречаются циклы по пустым переходам, автомат выполнит не более sn_r переходов. После этого до "зацикливания" автомат выполнит не более n_r+n_s переходов. Тем самым, всего получается время ожидания ((s+1)n_r+n_s)t, совпадающее с тайм-аутом на ожидание обязательной реакции, что и следовало ожидать. Мы можем увеличить это время, допуская, чтобы циклы проходились не более k₁ раз: ((s+1)n_r+n_s)t + k₁nt.

 

Алгоритм тестирования получается такой:

1)      На весь шаг тестирования (на все квази-конечное входное слово) устанавливается время ожидания t₁=((s+1)n_r+n_s)t+k₁nt.

2)      На ожидание каждой реакции также устанавливается тайм-аут t₀=((s+1)n_r+n_s)t+k₀nt.

3)      Если очередная i-ая реакция u[i] принята до истечения тайм-аута t₀, то она проверяется по словарной функции: u[1..i]ÎW(w).

a.       Если реакция неправильная, фиксируется ошибка.

b.      Если реакция правильная и время t₁ не истекло, то ожидаем следующую реакцию - п.2.

c.       Если реакция правильная и время t₁ истекло, то - п.5.

4)      Если очередная i-ая реакция u[i] не принята до истечения тайм-аута t₀, то проверяется, что она необязательна: u[1..i-1]ÏW(w).

a.       Если реакция обязательная, то фиксируется ошибка.

b.      Если реакция необязательна, то дожидаемся истечения времени t₁ или появления реакции.

                                                               i.      Если появилась необязательная i-ая реакция u[i], то она проверяется по словарной функции: u[1..i]ÎW(w). Далее пп.3a,3b,3c.

                                                             ii.      Если время t₁ истекло, то - п.5.

5)      Время t₁ истекло. Дальше ждать бессмысленно: время ожидания может быть бесконечным. Заканчиваем шаг тестирования, предполагая ("презумпция невиновности"), что реакции, которые поступят позже (быть может, бесконечное число реакций), правильные.

4.9.3. Автоматы с конечными выходными словами для квази-конечных входных слов

Естественный интерес представляют автоматы, в которых для каждого квази-конечного входного слова все выходные слова конечны. Заметим, что это свойство есть свойство самой словарной функции автомата. Легко показать, что необходимым и достаточным условием того, что автомат класса A2 обладает этим свойством, является следующее условие: в автомате нет циклов, которые содержали бы посылающие переходы и не содержали бы x-переходов (принимающих переходов по непустым стимулам).

4.10. Проблема постсостояния

Шаг адаптивного тестирования заключается в подаче на реализационный автомат квази-конечного входного слова, получения выходного слова (дополнительно, возможно, множества сериализаций) и анализа как с целью определения правильности полученных реакций, так и с целью определения в зависимости от них следующего квази-конечного входного слова. До сих пор мы предполагали, что в начале каждого шага реализационный автомат находится в начальном состоянии. Однако, в конце шага автомат может оказаться в другом состоянии и поэтому мы должны либо 1) перевести автомат в начальное состояние, либо 2) следующий шаг тестирования начинать не в начальном состоянии.

 

1. Для перевода автомата в начальное состояние v₀ обычно предполагается существование специальной операции reset. Ее можно рассматривать как особый стимул автомата, который допустим в каждом состоянии v для принимающего перехода (v,reset,v₀).

 

2. Если для автомата нет операции reset, мы вынуждены следующий шаг тестирования начинать в том состоянии (постсостоянии), в которое автомат попадает в конце предыдущего шага. Иногда это приходится делать и при наличии операции reset, например, если она слишком дорогая (по времени выполнения) или допустима не во всех состояниях. Соответственно, понятия входного слова, выходного слова, выполнения автомата, сериализации и маршрута используются не только для начального состояния, но и для любого состояния автомата. Точно также словарная функция может быть определена для любого состояния. По окончании шага тестирования мы должны, прежде всего, идентифицировать постсостояние. Заметим, что в общем случае таких возможных постсостояний может быть несколько и в каком именно из них находится реализационный автомат мы можем не знать. Сначала рассмотрим два частных случая: наличие специальных средств для определения постсостояния; наличие возможности однозначно вычислить постсостояние.

═

2.1. Тестированием с открытым состоянием будем называть такое тестирование, при котором у нас имеется специальная операция чтения постсостояния реализационного автомата. Сначала рассмотрим автоматы класса A5: любое квази-конечное слово переводит автомат в стационарное состояние: терминальное состояние или принимающее состояние без e-переходов в другие состояния (есть только e- петля). Очевидно, что это относится к выполнению автомата, начинающемуся не только в начальном, но и в любом состоянии, достижимом из начального по допустимому входному слову. В таких автоматах после шага тестирования мы можем прочитать постсостояние, которое является стационарным.

 

Если же автомат не относится к классу A5, то он может попасть в цикл из пустых, посылающих и e-переходов, и прочитанное состояние является лишь ╚мгновенным снимком╩ - автомат уже может перейти в другое состояние. Это общий случай множества возможных постсостояний.

 

2.2. Сильно-детерминированным асинхронным автоматом назовем автомат класса A5, в котором стационарное постсостояние однозначно определяется допустимым квази-конечным входным словом. Для классического автомата Мили это сильно-детерминированность совпадает с детерминированностью в обычном смысле. Слабо-детерминированным асинхронным автоматом назовем автомат класса A5, в котором стационарное постсостояние однозначно определяется парой из допустимого квази-конечного входного слова и выходного слова. Очевидно, что это относится к выполнению автомата, начинающемуся не только в начальном, но и в любом состоянии, достижимом из начального по допустимому входному слову. В таких автоматах после шага тестирования мы можем по модели однозначно вычислить единственное стационарное постсостояние. Заметим, однако, что, в отличии от тестирования с открытым состоянием, здесь мы имеем лишь гипотезу о том, что реализационный автомат находится в том же единственном постсостоянии, что и модель. Другое дело, что гипотеза о допустимости позволяет нам подавать в этом состоянии любое допустимое в модельном постсостоянии входное слово.

 

В общем случае мы уже не можем говорить о единственном постсостоянии, а только о множестве возможных постсостояний, в одном из которых═ автомат находится в данный момент времени после окончания шага тестирования. Если автомат относится к классу A5, но не является слабо-детерминированным, все эти возможные постсостояния стационарны. В противном случае, среди них могут быть и нестационарные состояния так, что автомат ожидает следующего непустого стимула не в каком-то, хотя и неизвестном, но одном состоянии, а непрерывно движется, меняя свое состояние и, быть может, выбирая из входной очереди пустые стимулы, то есть, проходя через рецептивные состояния. При наличии множества возможных постсостояний, входное слово, которое мы можем давать на следующем шаге тестирования, должно быть допустимо в любом из этих возможных постсостояний.

═4.11. Проблема имплицитной спецификации модели и обход графа состояний

До сих пор мы предполагали, что модельный автомат задан явно, например, в виде своего графа состояний. Однако, на практике модель часто задается имплицитно в виде спецификаций пред- и постусловий. Предусловие √ это логическое выражение от состояния и стимула, описывающее допустимость некоторых стимулов в некоторых состояниях автомата. Совокупность предусловий описывает полностью допустимость стимулов в состояниях автомата. Постусловие для асинхронных автоматов описывает переходы: постусловие принимающих переходов √ логическое выражение от пресостояния, стимула и постсостояния; постусловие посылающих переходов √ логическое выражение от пресостояния, реакции и постсостояния; постусловие пустых переходов √ логическое выражение от пресостояния и постсостояния. Совокупность постусловий вместе с соответствующими им предусловиями описывает все переходы автомата.

 

Задача построения графа состояний модельного автомата по его имплицитной спецификации сводится к решению системы уравнений имеющих вид pre(v,x)Þpost(v,x,v`), pre(v)Þpost(v,y,v`) или pre(v)Þpost(v,v`). Понятно, что такая задача может оказаться слишком сложной и не всегда решается удовлетворительным способом. С другой стороны, в процессе тестирования нам может не потребоваться весь модельный граф, поскольку, во-первых, не все реакции, разрешаемые моделью, обязаны присутствовать в реализационном автомате, и, во-вторых, не все реакции, разрешаемые реализацией, реально появятся в данном сеансе тестирования. Подграф модели, соответствующий данному сеансу тестирования, будем называть подграфом тестирования.

 

Можно поставить задачу построения подграфа тестирования в процессе самого тестирования. Проиллюстрируем возможный способ решения этой задачи для стационарного тестирования с открытым состоянием автомата класса A5 (в котором каждое стационарное состояние каждым допустимым квази-конечным словом переводится только в стационарные состояния). Для простоты будем считать также, что модель не имеет смешанных состояний. Пусть на некотором шаге тестирования автомат находится в стационарном состоянии a, подается стимул x, получается в ответ выходное слово u длины n и определяется стационарное постсостояние b. В графе модели этой ситуации соответствует множество маршрутов, начинающихся в состоянии a, заканчивающихся в состоянии b, имеющих x-раскраску xe^* и y-раскраску u. Получая на каждом шаге тестирования все такие маршруты мы в итоге получим требуемый подграф тестирования.

 

Маршруты шага тестирования можно получить, последовательно решая уравнения спецификации. Сначала решаем уравнение принимающего перехода pre(a,x)Þpost(a,x,v₁) относительно постсостояния v₁. Таких решений может быть несколько. Для каждого из этих решений v₁ независимо рассматриваем уравнение e-перехода pre(v₁,e)Þpost(v₁,e,v₂), посылающего перехода для 1-ой реакции═ pre(v₁)Þpost(v₁,u[1],v₂) и уравнение пустого перехода pre(v₁)Þpost(v₁,v₂) и независимо решаем их относительно постсостояния v₂. Если все эти уравнения не имеют решений, решение v₁ нужно отбросить. В противном случае, мы имеем множество решений v₂. Теперь для каждого решения v₂ рассматриваем═ независимо уравнения e-перехода pre(v₂,e)Þpost(v₂,e,v₃), посылающего перехода для 2-ой реакции═ pre(v₂)Þpost(v₂,u[2],v₃) √ если v₂ было решением посылающего перехода для 1-ой реакции, или pre(v₂)Þpost(v₂,u[1],v₃) √ если v₂ было решением пустого или e-перехода, а также уравнение пустого перехода pre(v₂)Þpost(v₂,v₃) и независимо решаем эти уравнения относительно постсостояния v₃. Этот процесс продолжается и дальше, но только на каждой ветви этого процесса, после того как будет решено уравнение посылающего перехода для последней реакции u[n] будем проверять, попало ли постсостояние b в число решений этого уравнения. Если попало, то эта ветвь заканчивается, а если нет, то продолжается решением уравнений только e-переходов и пустых переходов пока таким решением не станет b.

 

Поскольку автомат относится к классу A5, это гарантирует завершение процесса вычислений за конечное время. Если постусловия имеют вид v`=f(v,x), v`=g(v,y) и v`=h(v), то решение уравнений сводится к вычислению всех значений многозначных функций f, g и h.

 

Аналогично можно строить подграф тестирования для стационарного тестирования слабо-детерминированного автомата класса A5, не требуя открытости состояния. Отличие в том, что вместо проверки на известное стационарное постсостояние мы будем проводить вычисления на каждой ветви до получения стационарных решений уравнений спецификации. (Вообще говоря, мы должны тестировать не только на квази-конечных словах с одним непустым стимулом, поэтому в решаемые уравнения нужно включить также уравнения для принимающих переходов по очередным стимулам входного слова.)

 

В обоих вариантах стационарного тестирования (с открытым состоянием или для слабо-детерминированного автомата) можно поставить задачу: в каждом достигнутом при тестировании стационарном состоянии попробовать каждый допустимый стимул. Более точно: попробовать квази-конечное слово вида xe^w для каждого непустого стимула x. Адаптивный алгоритм с таким свойством будем называть обходом графа по стимулам.

 

Мы можем потребовать большего. Назовем неразделяемым маршрут выполнения для допустимого квази-конечного входного слова, ведущий из стационарного пресостояния v в стационарное постсостояние v`, все внутренние состояния которого нестационарны. Соответствующее квази-конечное входное слово (x-раскраска маршрута) назовем неразделяемым словом для состояния v. Мы можем потребовать при тестировании прохода по всем стационарным состояниям, которые можно достигнуть из данного стационарного состояния по всем неразделяемым квази-конечным словам. Для этого в каждом состоянии мы должны попробовать такое подмножество квази-конечных входных слов, чтобы гарантированно достигнуть все такие стационарные состояния. Адаптивный алгоритм с таким свойством будем называть обходом графа по неразделяемым словам.

 

Понятие обхода по неразделяемым словам можно обобщить на случай произвольного асинхронного автомата.═ Здесь возникают две задачи: 1) описать классы автоматов, для которых существует такой обход, и 2) найти эффективные алгоритмы построения обходов одновременно с построением самого графа тестирования. В общем случае эти задачи не решены.

4.13. Проблема медиаторов и многоуровневые спецификации

До сих пор мы предполагали, что алфавиты стимулов и реакций модельного и реализационного автоматов совпадают. На практике это часто не так═ и для установления соответствия реализации и модели используются специальные медиаторные преобразования (медиаторы). Алфавитным медиатором назовем медиатор, который осуществляет простое ображение j модельного алфавита стимулов в реализационный алфавит стимулов и отображение y реализационного алфавита реакций в модельный алфавит реакций. Эти отображения естественно расширяются на последовательности стимулов и реакций. Тогда сводимость реализации к модели записывается так: Dom(W[R])Êj(Dom(W)) "wÎDom(W) y(W[R](j(w)))ÍW(w).

 

В общем случае могут быть и другие (неалфавитные) медиаторы, которые сразу определяются как отображения входных и выходных слов с сохранением требования о равенстве длин модельного и реализационного слов. Более того, эти отображения могут быть многозначными и тогда более естественно говорить о медиаторных соответствиях. Эти соответствия должны обладать определенными свойствами, в частности, соответствующие слова являются продолжениями соответствующих слов. Кроме того, имеет смысл говорить о регулярных соответствиях, то есть, о соответствиях, которые могут быть заданы как множества, порождаемые конечными графами.

 

Кроме того, сами спецификации могут быть многоуровневыми так, что каждый уровень соответствует некоторому уровню абстракции и формулирует функциональные требования соответствующего уровня. Наиболее частая ситуация √ три уровня: 1) уровень реализации, 2) уровень спецификации в виде пред- и постусловий и 3) уровень тестовой модели, которая является в некотором смысле фактор-моделью спецификационной модели, не имеет описания не только в виде графа состояний, но и в виде пред- и постусловий, а задается только медиаторным соответствием с уровнем спецификации; по тестовой модели происходит непосредственное тестирование.

 

 

 

5. Заключение

 

Понятие асинхронного автомата является удобной математической абстракцией для спецификации программных и аппаратных систем, имеющих свойства ╚автоматности╩, но более сложных, чем классические автоматы Мили. В то же время теория таких автоматов и, особенно,═ методы тестирования соответствия для таких автоматов находятся пока что в зачаточном состоянии.

 

В настоящей статье мы дали определение асинхронного автомата и его выполнения, ввели классификацию автоматов с точки зрения реализуемой ими словарной функции и рассмотрели некоторые вопросы реализации словарной функции такими автоматами в виде множества сериализаций √ смешанных последовательностей вопринимаемых стимулов и выдаваемых реакций.

 

Что касается тестирования соответствия, то мы лишь обозначили некоторые возникающие здесь проблемы и наметили некоторые возможные пути их решения. Реальные эффективные алгоритмы существуют лишь для некоторых частных (хотя, возможно, и широко распространенных) классов асинхронных автоматов. В дальнейшем мы предполагаем уделить этому вопросу большее внимание.

 

Асинхронные автоматы √ это автоматы с одной входной и одной выходной очередями. Естественный следующий шаг √ рассмотреть автоматы с несколькими очередями. После этого можно изучать сети автоматов, в которых каждая очередь является выходной очередью одного или нескольких автоматов и входной очередью также одного или нескольких автоматов. Такие автоматные сети можно использовать как модель программных и аппаратных систем с несколькими независимыми активностями (процессами), поведение каждой из которых можно моделировать отдельным асинхронным автоматом. Здесь возникают не только проблемы тестирования таких сетей, но и проблемы их спецификации, которые можно рассматривать также как не только чисто функциональные, но и композиционные (структурные).

 

Литература:

 

1.      G. Karjoth. XFSM : A formal model of communicating state machines for implementation specifications. In D. Etiemble, J.C. Syre, editors, PARLE'92 ``Parallel Architectures and Languages Europe'' Springer Verlag, Lecture Notes in Computer Science 605, pages 979-980, 1992.

2.      Alan C. Shaw. Communicating Real-Time State Machines. IEEE TRANSACTIONS ON SOFTWARE ENGINEERING, VOL. 18, NO. 9, SEPTEMBER 1992

3.      Gregor V. Bochmann , Alexandre Petrenko, Protocol testing: review of methods and relevance for software testing, Proceedings of the 1994 international symposium on Software testing and analysis, p.109-124, August 17-19, 1994, Seattle, Washington, United States

4.      D. Lee and M. Yannakakis. Principles and methods of testing finite state machines - a survey. In Proceedings of the IEEE, volume 84, number 8, pages 1090-1123, Berlin, Aug 1996. IEEE Computer Society Press.

5.      YoungJoon Byun, Beverly A. Sanders, and Chang-Sup Keum. " Design Patterns of Communicating Extended Finite State Machines in SDL". In Proceedings of the 8^th Conference on Pattern Languages of Programs, Monticello, Illinois, September 2001.

6.      Naveen Chandra R, Verification of Communicating Reactive State Machines, M.Tech. Thesis, IIT Bombay, Jan. 2002, Guide: Prof. S. Ramesh.

7.      Рабин М., Скотт Д., Конечные автоматы и проблемы их разрешения. Кибернетический сборник, ИЛ, вып. 4 (1962), 58-91.

8.      Сеймур Гинзбург. Математическая теория контекстно-свободных языков. М., ╚МИР╩, 1970, 71-78.

9.      Д.В.Варсанофьев, А.Г.Дымченко. Основы компиляции. 1991. http://www.codenet.ru/progr/compil/cmp/intro.php