Игорь Бурдонов
Магические квадраты, булева алгебра и «Книга Перемен»
(Доклад на 2-ой научной конференции «И цзин и современность»)
Толчком к настоящей работе послужили два обстоятельства.
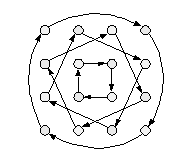
1). Магические квадраты. Постоянное, я бы сказал, навязчивое сопоставление квадратно-кругового расположения триграмм (фиг.1) с магическим квадратом Ло Шу (фиг.2). Это сопоставление не только традиционно, но и поддерживается многими современными исследователями [1, стр.23,26,27]. Причина и цель такого сопоставления не вполне ясны. Само по себе пространственное расположение триграмм в периферийных клетках девятиклеточного квадрата вполне естественно. Но какую роль тут играет именно магичность числового квадрата Ло Шу? Напомним, что магичным называется квадрат nxn, клетки которого заполнены числами от 1 до n2 и сумма чисел в каждом ряду (строке, столбце, диагонали) одна и та же – «магическая» – сумма (n2+1)n/2.
|
|
||||||||||||||||||
|
Фиг.1. Расположение триграмм по Вэнь-вану |
Фиг. 2. Квадрат Ло Шу |
2). Логика, точнее, простейшая ее часть, формализованная в виде булевой алгебры, наиболее известными интерпретациями которой являются алгебра высказываний и алгебра множеств. Здесь оказались полезными рассуждения А.И.Кобзева о китайской протологике и, в частности, о двух видах отрицания: контрарном и контрадикторном [2, гл.3, §2].
Не вдаваясь в дискуссию о правильном наименовании китайской системы «символов и чисел», мы будем условно называть ее «нумерологией» с подразумеваемыми кавычками. По Кобзеву, в Европе логика победила нумерологию (Платон - Пифагора), а в Китае, наоборот, нумерология - логику (протологику). Глубинная причина: идеализм в Европе и натурализм в Китае. Логика основана на законе тождества, а тождества в реальном (натуральном) мире нет: любые две конкретные вещи нетождественны. Тождественны могут быть лишь идеальные конструкты, эйдосы. По этой же причине: в Европе - диалектика, в Китае - псевдодиалектика Лао-цзы, мышление "инь-ян", мышление в противоположностях, биполярное мышление. Диалектика, преодолевая логический закон противоречия ("исключённое третье"), не способна преодолеть закон тождества. Вторая причина: ориентация в Европе на субстанциальную картину мира - "мир вещей", и ориентация в Китае на процессуальную картину мира - "мир перемен".
В целом выстраиваются оппозиции:
|
Европа |
Китай |
|
тождество |
подобие |
|
противоречие |
противоположность |
|
субстанция |
процесс |
|
логика |
нумерология |
|
диалектика |
биполярное мышление |
|
определение через род и видовое отличие |
определение с помощью антонимов |
|
сущность |
отношение |
|
исследование одного объекта |
исследование соотношения разных объектов |
|
контрадикторное
отрицание |
контрарное (оппозиционное) отрицание |
|
"не-лошади" - это весь универсум |
"не-лошади" - это остальные представители "рода" 6 видов домашних животных: коровы, овцы, куры, собаки, свиньи |
Специально для двух видов отрицания можно провести следующее сопоставление:
|
Контрадикторное отрицание |
Контрарное отрицание |
|
абсолютное отрицание |
утверждение противоположного |
|
безгранично (выводит за пределы): |
ограниченно (оставляет в пределах): |
|
не-A - это "всё", кроме A: |
не-A - это B противоположное A: |
|
если A "вещь", то не-A "не вещь" |
если A "вещь", то не-A "тоже вещь" |
|
Противоречие безусловно: |
Противоположность условна |
|
Операция отрицания унарна: |
Операция отрицания бинарна: |
|
Отношение отрицания бинарно: |
Отношение отрицания тринарно: |
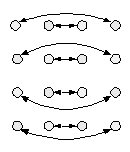
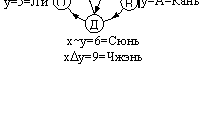
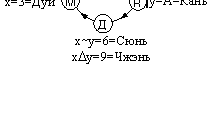
Интересная картина получается для частичного отрицания, когда объект определяется двумя признаками и рассматриваются возможные сочетания отрицания или утверждения каждого из этих признаков (фиг.3 и 4).
|
|
|||||||||||||
|
Фиг. 3. Контрадикторное отрицание |
Фиг.4. Контрарное отрицание |
Как видим, для контрарного отрицания выстраивается схема девятиклеточного квадрата.
|
16 |
3 |
2 |
13 |
|
5 |
10 |
11 |
8 |
|
9 |
6 |
7 |
12 |
|
4 |
15 |
14 |
1 |
|
Фиг. 5 |
|||
Возвращаясь к магическим квадратам, заметим, что в Европе наиболее популярны были квадраты 4-го порядка, то есть, квадраты 4x4. Пожалуй, самым знаменитым можно считать числовой квадрат, изображенный на знаменитой гравюре Альбрехта Дюрера «Меланхолия» (фиг.5).
|
x |
= |
0011 |
= |
316 |
|
y |
= |
0101 |
= |
516 |
|
& |
= |
0001 |
= |
116 |
|
ùx |
= |
1100 |
= |
C16 |
|
y\x |
= |
0100 |
= |
416 |
|
Фиг. 6 |
||||
Попробуем сопоставить клетки квадрата Дюрера и логические операции булевой алгебры. Алгеброй E2 называют булеву алгебру над множеством из двух элементов «истина» и «ложь», называемых логическими значениями. Здесь возможны 16 логических операций как логических функций, то есть, функций принимающих логическое значение, от двух агрументов, каждое из которых также принимает значение «истина» или «ложь». В свою очередь, как булева алгебра E16 может рассматриваться само это множество 16 логических функций, являющихся как аргументами, так и значениями логических операций. Для сопоставления с числами в клетках квадрата Дюрера воспользуемся кодировкой логических функций, основанной на кодировке аргументов x и y (пример на фиг.6). С помощью такой кодировки мы получаем отождествление 16 логических операций с шестнадцатиричными цифрами (их обозначают десятичными цифрами от 0 до 9 и далее латинскими буквами A,B,C,D,E,F). Тогда вместо обычной записи ùx&y=y\x можно записывать в двоичном коде: ù00112&01012 = 11002&01012 = 010016 или в 16-ричном коде: ù316&516 = C16&516 = 416. Более того, учитывая, что код конъюнкции 00012=116, можно записать 110020001201012 = 01002 или C16116516 = 416. Фактически, такая кодировка определяет булеву алгебру шестнадцатиричных цифр изоморфную алгебре логических функций, что позволяет говорить о структурном тождестве чисел и логических операций.
Теперь запишем квадрат Дюрера шестнадцатиричными цифрами, предварительно уменьшив каждое число на «1», чтобы получить числа от 0 до 15 (магичность квадрата при этом сохраняется) – фиг.8. После этого можно каждую 16-ричную цифру рассматривать как код логической операции – фиг.7. Учитывая двоичный код 16-ричной цифры, можно тот же квадрат представить с
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Фиг.7 |
Фиг.8 |
Фиг.9 |
помощью тетраграмм: целая черта ян соответствует «1», прерванная черта инь – «0»; нижняя позиция тетраграммы соответствует младшему разряду числа, а верхняя позиция – старшему разряду – фиг.9 (прочтение тетраграммы снизу вверх, соответствует прочтению двоичного числа справа налево – от младших разрядов к старшим).
Квадрат Дюрера обладает двумя важными свойствами, которые имеют как «логический», так и «нумерологический» смысл, то есть, могут быть естественным образом интерепретированы как в терминах логических операций, так и в терминах тетраграмм.
|
&=116=00012= |
|
= |
ù |
|
=ù11102=ùE16=ù |
|
Фиг.10 |
|||||
Первое такое свойство – симметричность (фиг.10). В числовом квадрате Дюрера центрально-симметричные клетки квадрата занимают пары чисел, сумма которых равна половине магической суммы. Соответствующие логические операции являются отрицаниями друг друга, например, «истина» и «ложь», или конъюнкция «&» и антиконъюнкция (штрих Шеффера) «». Соответствующие тетграграммы получаются друг из друга инверсией каждой черты (инь-ян, ян-инь). В ицзинистике связь через центр обозначается специальным техническим термином цо, а противоположность черт – дуй. Считается, что они относятся к, так называемому, «прежнему небу». Таким образом, можно говорить о «преднебесности» отрицания, что, видимо, означает фундаментальную природу этой логической операции. Действительно, первый акт самосознания есть различение «я» и «не-я», то есть, восприятие внешнего мира как отрицание субъекта; само выделение объекта из космического континуума основано также на отрицании: объект и не-объект.
Второе свойство – равномерность (фиг.11). В числовом квадрате Дюрера четыре числа в одном ряду, сумма которых равна магической сумме, имеют в каждом двоичном разряде ровно две «единицы» и два «нуля». Для тетраграмм это означает наличие в каждой позиции двух черт ян и двух черт инь. Для логических
|
a=F16 |
b=216 |
c=116 |
d=C16 |
|
|
|
|
|
|
a&b&c&d=0 |
aÚbÚcÚd=F |
||
|
aDbDcDd=0 |
a~b~c~d=F |
||
|
Фиг.11 |
|||
операций равномерность эквивалентна константным значениям всех четырех (не вырожденных до унарных или нуль-арных) коммутативных и ассоциативных операций: конъюнкции, дизъюнкции, исключающей дизъюнкции и эквивалентности. В число рядов клеток входят стороны квадрата, а для расположения триграмм в девятиклеточном квадрате стороны квадрата – единственные ряды из трех триграмм, поскольку центральная клетка остается пустой. В ицзинистике связь по окружности или сторонам квадрата обозначается специальным техническим термином цзун. Свойство равномерности ряда тетраграмм инвариантно к перестановке позиций (синхронно во всех четырех тетраграммах), а важный частный случай такой перестановки, когда происходит полный «переворот» позиций (для тетраграмм позиции 1234 переходят в позиции 4321) обозначается термином фань. Считается, что цзун и фань относятся к, так называемому, «последующему небу». Таким образом, можно говорить о «посленебесности» равномерности, что, видимо, означает менее фундаментальную по сравнению с отрицанием природу бинарных коммутативных и ассоциативных логических операций. Действительно, такие операции связывают два объекта, которые предварительно должны быть выделены с помощью отрицания из космического континуума.
Симметричность и равномерность характерны не только для квадрата Дюрера. И хотя не все магические квадраты симметричны или равномерны, квадраты с этими свойствами занимают совершенно особое место среди всех магических квадратов 4-го порядка (в частности, все равномерные квадраты – магические). Соотношение квадратов разных видов представлено на фиг.12, числовые характеристики – на фиг.13.
|
Число квадратов 4-го порядка
|
||||||||||||||||||||||||||||||||||||
|
Фиг.12 |
Фиг.13 |
||||||||||||||||||||||||||||||||||||
Как только речь заходит о множестве объектов с общим свойством, полезно изучать преобразования объектов, сохраняющие это свойство. Для свойства «магичности» квадратов, прежде всего, выделяются повороты на 90° и симметрии относительно горизонтальной или вертикальной оси. Таким способом из каждого магического квадрата можно получить восемь магических квадратов (включая исходный). Восьмичленный набор квадратов, порождаемый квадратом Ло Шу, исчерпывает собой все магические квадраты 3-го порядка. Для квадратов 4-го порядка ситуация совершенно иная. Кроме восьмичленного набора квадрата Дюрера имеется еще 879 наборов.
Нас будут особо интересовать преобразования квадратов 4-го порядка, которые сохраняют симметричность и равномерность и которые в известном смысле можно считать «логическими», поскольку они допускают естественную интепретацию в терминах логических операций. Каждое преобразование описывает способ получения нового значения (числа, тетраграммы или логической операции) в каждой клетке квадрата как функции от старого значения. Эти логические преобразования являются композициями преобразований двух видов: инверсии и перестановки.
Преобразование инверсии – в терминах тетраграмм – изменение нескольких (от 0 до всех 4-х) черт на противоположные. Кроме указанной выше операции дуй – изменение всех черт, подобные преобразования встречаются в древней литературе для гексаграмм и иного числа черт. Сам стандартный способ гадания по «Книге Перемен», зафиксированный в «Си цы чжуани», предполагает выпадение одной гексаграммы и выделение в ней некоторого числа позиций (от 0 до 6), в которых находятся «старые» черты, изменяемые на противоположные. Согласно данным А.И.Кобзева [1], в «Цзо чжуани» десять случаев описывают пары гексаграмм, отличающихся одной чертой, и один случай – пару гексаграмм, отличающихся пятью чертами, «Го юй» содержит два случая, когда гексаграммы различаются тремя чертами. Кобзев предполагает, что здесь имеется в виду некая отличная от стандартной система гадания, аналогичная системе Шао Юна, но созданная не в эпоху Сун (X-XIII вв.), а гораздо раньше и применявшаяся уже во времена Чунь-цю.
В терминах логических операций инверсия – это исключающая дизъюнкция uDT, где u –изменяемая логическая операция (или ее код), а логическая операция T описывает способ изменения – код T содержит «1» в изменяемых позициях, выделяя «старые» черты тетраграммы. В зависимости от значения T, имеется 24=16 различных операций инверсии. В частности, операция дуй = uD«истина» = uD11112 = uDF16. Преобразование инверсии – «преднебесное».
Преобразование перестановки – в терминах тетраграмм – перестановка черт тетраграммы, то есть, когда новая тетраграмма состоит из тех же черт, но помещенных в другие позиции. Операция фань для тетраграмм является частным случаем перестановки, когда меняются местами черты в позициях 1-4 и 2-3. Для гексаграмм в расположении Вэнь-вана операцией фань связаны соседние гексаграммы (с номерами 2n-1 и 2n).
В терминах логических операций перестановка – это подстановка u(P,Q), где u - изменяемая логическая операция (или ее код), а P и Q – две логические операции от x и y, подставляемые вместо аргументов x и y. Для того чтобы подстановка u(P,Q) определяла взаимно-однозначное преобразование, то есть, преобразовывала 16 различных логических операций (или их кодов – чисел) снова в 16 различных значений, нужно, чтобы следующие четыре операции не были тождественно-ложными: P&Q¹0, P¯Q¹0, P\Q¹0, Q\P¹0. В зависимости от возможных значений P и Q, имеется 4!=24 различных операций перестановки. В частности, операция фань(u) = u(ùx,ùy) = u(11002,10102) = u(C16,A16). Преобразование перестановки – «послебесное».
Перестановки тесно связаны с выбором способа кодировки логических функций. Тот способ, который указан на фиг.6, не является единственно возможным. Этот способ определяется порядком перечисления пар значений аргументов x и y: 00, 01, 10, 11, что определяет кодировку самих аргументов, точнее, логических функций, тождественно равных одному из своих аргументов: x=3(x,y), y=5(x,y). Числа 3 и 5 являются важнейшими в китайской нумерологии. Достаточно отослать к 4-ой главе книги А.И. Кобзева [2], которая так и называется "Универсальная троично-пятеричная модель мироздания". Вместе с тем понятно, что может быть выбран любой другой из возможных 4!=24 порядков перечисления пар значений аргументов. Например, при перечислении 00, 01, 11, 10 аргументы кодируются x=3, y=6, а, например, конъюнкция получает код не «1», а «2». Вообще, годится любая пара кодов аргументов, если она удовлетворяет следующему условию: при переборе всех четырех разрядов кодов перебираются (в любом порядке) все четыре различные пары 00, 01, 10 и 11. Этому условию не удовлетворяет, например, пара кодов 2 и 3. Хотя это тоже важнейшие нумерологические числа (первое чётное и первое нечётное числа; символы Земли и Неба и т.п.), однако их недостаточно; для логики требуется пара 3 и 5 (или другая производная от этой пара).
Каждый такой способ кодировки взаимно-однозначно связан с соответствующим преобразованием перестановки u(P,Q): новые коды аргументов x и y соответствуют старым кодам операций P и Q. На фиг.14 представлены все возможные преобразования перестановки и,
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Фиг.14 |
Фиг.15 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
соответственно, способы кодировки. Фиг.15 показывает, что в той или иной форме числа 3 и 5 присутствуют и в любой другой кодировке: здесь коды аргументов представлены в разложении на числа 2,3 и 5. Видно, что в каждом разложении присутствуют числа 3 и 5 – последнее, возможно, в виде еще двух чисел 2 и 3, сумма которых и есть 5 – а также, быть может, еще несколько двоек (от 0 до 3-х). Следует подчеркнуть, что по нумерологическим правилам 3 и 5 являются репрезентантами целого класса чисел: 3=6,9,12,18,27,81,... и 5=10,25,50,100,125,... Для шестнадцатиричных цифр получается 3=6,9,C и 5=A – эти и только эти цифры комбинируются различными способами в допустимых кодировках аргументов.
Преобразования квадратов являются элементами группы подстановок (взаимно-однозначных отображений множества в себя) 16-го порядка (умножение преобразований определяется как их последовательное выполнение). Сам числовой квадрат k также
|
[0,0]=0 |
[0,1]=1 |
[0,2]=2 |
[0,3]=3 |
|
[1,0]=4 |
[1,1]=5 |
[1,2]=6 |
[1,3]=7 |
|
[2,0]=8 |
[2,1]=9 |
[2,2]=A |
[2,3]=B |
|
[3,0]=C |
[3,1]=D |
[3,2]=E |
[3,3]=F |
|
Фиг.16. |
|||
является такой подстановкой и может рассматриваться как преобразование из некоторого стандартного квадрата (фиг.16), в котором в каждой клетке находится ее номер: [i,j]=(4i+j)®k[i,j]. Поэтому применение преобразования значений j к числовому квадрату k есть произведение kj. Соответственно, и преобразование, в частности, логическое может рассматриваться как числовой квадрат, а именно, тот, который получается этим преобразованием из стандартного квадрата.
Преобразования, о которых до сих пор шла речь, можно назвать преобразованиями значений – они определяют новое значение в каждой клетке квадрата как функцию от старого значения. Существует и другой класс преобразований квадратов – преобразование клеток: если клетки квадрата перенумеровать стандартным образом (фиг.16), то преобразование определяет номер новой клетки, в которое перемещается значение из старой клетки, как функцию номера старой клетки. Это удобно изображать стрелками ведущими из старой клетки в новую.
|
|
|
|
Фиг.17. |
Фиг.18. |
Преобразования поворота квадрата на 90° (фиг.17) и симметрии относительно вертикальной (фиг.18) или горизонтальной оси являются частными случаями таких преобразований клеток. Среди преобразований клеток также можно выделить логические преобразования двух видов – инверсии и перестановки, определяемые аналогичным образом: в формулах uDT и u(P,Q) аргумент u – это номер старой клетки, а числовое значение операции – номер новой клетки. Преобразование клеток y также является подстановкой 16-го порядка, но только применяемой не к содержимому, а к номерам клеток, и связано с преобразованием значений j, дающим для квадрата k тот же результат, соотношением kj=y-1k.
На фиг.19 показана связь логических преобразований с квадратами разных видов. Мы видим, что логические преобразования значений сохраняют равномерность (Р) и симметричность (С) квадратов. И хотя существуют неравномерные магические (М)
|
Преобразования |
|
|
значений |
клеток |
|
СР ® СР |
СР ® СР |
|
С ® С |
С ® С |
|
Р ® Р |
Р и неС ® неР |
|
неР ® неМ |
|
|
Фиг.19 |
|
квадраты, такие квадраты «логически неустойчивы» – каждый из них некоторым логическим преобразованием значений переводится в немагический квадрат. Логическое преобразование клеток сохраняет симметричность квадрата, равномерный симметричный квадрат преобразуется также в равномерный симметричный квадрат. Однако, равномерные несимметричные квадраты менее «устойчивы» – каждый из них некоторым логическим клеток переводится в неравномерный квадрат. Сами логические преобразования (L), рассматриваемые как числовые квадраты, являются симметричными немагическими квадратами (фиг.12) и связаны с симметричными равномерными квадратами (СР) соотношением L=(СР)2; квадраты обратные (в смысле преобразований) СР-квадратам также являются СР-квадратами (СР)-1=СР; логические квадраты и СР-квадраты вместе образуют подгруппу группы подстановок (минимальную, содержащую СР-квадраты).
Завершая на этом анализ магических квадратов 4-го порядка, мы видим, что они поддаются хорошей интерпретации как в терминах логических операций, так и в терминах тетраграмм. Возвращаясь к триграммам, можно сформулировать следующую проблему: нельзя ли провести аналогичное сопоставление триграмм и логических операций? Трудность здесь в том, что триграмм восемь, а логических операций шестнадцать. Следовательно, мы должны попытаться выбрать подмножество логических операций или каким-то образом попарно отождествить логические операции, чтобы получить восемь пар. Можно предложить два естественных способа выборки восьми логических операций.
Первый способ – наложить такое ограничение на аргументы логических операций, при котором операции попарно отождествляются. Для этого нагляднее всего воспользоваться теоретико-множественной интерпретацией логических операций. Аргументы x и y представляются двумя
|
|
|
черта 4 : 8 = x ¯ y = ù (xÈy) |
||
|
|
черта 2 : |
2 = x \ y |
|
|
|
|
|
черта 1 : 1 = x&y = xÇy |
|
|
|
|
|
черта 3 : |
4 = y \ x |
|
|
|
|
|
|
|
|
Фиг.20 |
||||
подмножествами некоторого множества, которые разбивают последнее в общем случае на четыре базовые области соответствующие парам «истинностных» значений 00, 01, 10 и 11 или четырем операциям: антидизъюнкция = дополнение объединения множеств, две разности x\y и y\x, конъюнкция = пересечения множеств (фиг.20). В терминах тетраграмм каждая из этих базовых областей соответствует выделению одной из четырех позиций: выделенная позиция занимается чертой ян, остальные – чертой инь.
Ограничение заключается в объявлении одной из базовых областей пустой, что эквивалентно объявлению тождественно ложной одной из четырех операций или удалению выделенной позиции из тетраграмм и, тем самым, превращению их в триграммы. При этом отождествляются те логические операции, коды которых отличаются в соответствующем (выделенном) разряде, то есть, те, которые принимают разные значения на выделенной паре истинностных значений аргументов, а на остальных парах – одинаковые значения. Соответственно, отождествляются две тетраграммы, отличающиеся лишь одной чертой, располагающейся в удаляемой позиции.
Например, удаление 1-ой (нижней) позиции тетраграммы эквивалентно объявлению тождественно-ложной операции конъюнкции x&y=«ложь». При этом отождествляются пары логических операций с кодами 0=1, 2=3, 4=5, 6=7, 8=9, A=B, C=D, E=F. В терминах базовых областей это означает, что пересечение областей x и y пусто, то есть, они не имеют общих точек. В логико-философском смысле это можно интерпретировать как несовместность двух объектов x и y. Мир, в котором все объекты несовместны, можно наглядно представить, если считать каждый объект плоскостной фигурой конечной площади (не обязательно связной). Мир как совокупность всех объектов характеризуется четырьмя параметрами: бесконечным (¥) или конечным (–) числом объектов; делимостью, которую можно понимать как бесконечное (¥) или конечное (–) число объектов на ограниченной площади; наличие (¥) или отсутствие (–) объектов сколь угодно больших размеров; наличие (¥) или отсутствие (–) объектов сколь угодно малых размеров. Не все сочетания параметров возможны. Например, конечное число оъектов определяет конечность всех остальных параметров, поэтому интерес представляют миры с бесконечным числом объектов. Для мира «несовместности», например, конечный размер мира определяет бесконечную делимость, отсутствие сколь угодно больших объектов и наличие сколь угодно малых объектов. На фиг.21 показаны все четыре «мира» и возможные параметры миров.
|
удаляемая позиция тетраграммы |
1 |
2 |
3 |
4 |
|||||||||||||||
|
тождественно-ложная операция |
x&y |
x\y |
y\x |
x¯y |
|||||||||||||||
|
отношение множеств |
x и y не пересекаются |
x вложено в y |
y вложено в x |
x È y = все множество |
|||||||||||||||
|
отношение объектов |
несовместность |
целое и часть |
взаимопроницание |
||||||||||||||||
|
число объектов |
– |
¥ |
¥ |
¥ |
¥ |
¥ |
¥ |
¥ |
¥ |
¥ |
– |
¥ |
¥ |
¥ |
¥ |
¥ |
– |
¥ |
|
|
делимость мира |
– |
¥ |
¥ |
¥ |
¥ |
¥ |
– |
– |
– |
– |
– |
¥ |
¥ |
¥ |
¥ |
– |
– |
¥ |
|
|
размер мира |
– |
– |
¥ |
¥ |
¥ |
¥ |
¥ |
¥ |
¥ |
¥ |
– |
– |
– |
¥ |
¥ |
¥ |
– |
– |
|
|
максимальный размер объектов |
– |
– |
¥ |
¥ |
– |
– |
¥ |
¥ |
– |
– |
– |
– |
– |
¥ |
¥ |
¥ |
– |
– |
|
|
минимальный размер объектов |
– |
¥ |
¥ |
– |
¥ |
– |
¥ |
– |
¥ |
– |
– |
¥ |
– |
¥ |
– |
– |
– |
– |
|
|
Фиг.21 |
|||||||||||||||||||
Особый интерес представляет мир 4, который всегда ограничен по размеру, но, при бесконечной делимости, способен содержать бесконечное число объектов, причем каждая пара объектов покрывает весь мир, объекты не вложены друг в друга и взаимопроницают друг друга. Не напоминает ли это символ «Великого Предела» (Тай-Цзи), в котором две фигуры покрывают круг («весь мир») и изображают инь и ян, которые не вложены друг в друга, но и не несовместны, поскольку взаимопроницаются маленькими кружками инь внутри ян и ян внутри инь, которые как бы принадлежат и одной и другой фигуре? Бесконечную последовательность фигур можно получить, если n-ую фигуру, начиная с n=3, определить как дополнение до большого круга части пересечения всех предыдущих n-1 фигур. Здесь возможны три варианта: 1) кружок «инь в ян» представляется как бесконечная цепь концентрических кружков все более меньшего радиуса и все фигуры, кроме первых двух, – это их дополнения до большого круга; 2) то же самое, но только для кружка «ян в инь», и 3) для обоих кружков. Эти три варианта можно сопоставить с первыми двумя гексаграммами «Книги Перемен» – «цепь неба» и «цепь земли», и парой последних гексаграмм, переходящих друг в друга по дуй и фань и содержащих равное число черт ян и инь, – «цепь человека».
Другой способ выделения 8-и логических операций из 16-и основан на понятии замкнутого подмножества операций, то есть, такого подмножества, которое вместе с любыми тремя операциями p,a,b содержит и их композицию p(a,b). Очевидно, все множество 16-и логических операций замкнуто, другим тривиальным примером являются одноэлементные подмножества «ложь» и «истина». Для наших целей интерес представляют замкнутые подмножества из 8-и операций. Таких подмножеств всего девять (фиг.22); они образуют 4 класса, поскольку последние 6 подмножеств получаются друг из друга с помощью перестановочного преобразования или выбора подходящей кодировки логических операций.
|
класс |
коды операций |
замкнутые подмножества |
«миры» |
||||||||||
|
1 |
2 |
3 |
4 |
||||||||||
A |
01234567 |
0 |
& |
x\y |
x |
y\x |
y |
D |
Ú |
|
|
|
14 |
|
B |
13579BDF |
& |
x |
y |
Ú |
~ |
yÞx |
xÞy |
F |
1 |
|
|
|
|
C |
03569ACF |
0 |
x |
y |
D |
~ |
ùy |
ùx |
F |
2 |
6 |
10 |
15 |
|
D |
03478BCF |
0 |
x |
y\x |
xÚy |
¯ |
yÞx |
ùx |
F |
3 |
7 |
|
|
|
02578ADF |
0 |
x\y |
y |
Ú |
¯ |
ùy |
xÞy |
F |
4 |
|
11 |
|
|
|
02469BDF |
0 |
x\y |
y\x |
D |
~ |
yÞx |
xÞy |
F |
5 |
|
|
16 |
|
|
016789EF |
0 |
& |
D |
Ú |
¯ |
~ |
|
F |
|
8 |
12 |
|
|
|
0145ABEF |
0 |
& |
y\x |
y |
ùy |
yÞx |
|
F |
|
9 |
|
17 |
|
|
0123CDEF |
0 |
& |
x\y |
x |
ùx |
xÞy |
|
F |
|
|
13 |
18 |
|
|
Фиг.22 |
|||||||||||||
На самом деле, оба способа выделения 8-и логических операций связаны друг с другом. В логическом смысле основным является 1-ый способ (базовые области), а выбор соответствующего замкнутого подмножества логических операций является "делом вкуса". Дело в том, что при отождествлении двух логических операций выбор основной (попадающей в подмножество) и производной (отождествляемой с основной, но не попадающей в подмножество) есть выбор той или иной нотации тождественных логических операций. Конечно, таких нотаций много (28=256), но мы рассматриваем только те, которые соответствуют замкнутым подмножествам логических операций, то есть подмножествам, "естественно" выделяемым и для общего случая (все базовые области непусты). Всего получается 18 возможных комбинаций обоих способов.
|
ложь |
x |
y |
xDy |
x~y |
ùy |
ùx |
истина |
|
0 |
3 |
5 |
6 |
9 |
A |
C |
F |
|
|
|
|
|
|
|
|
|
|
кунь |
дуй |
ли |
сюнь |
чжэнь |
кань |
гэнь |
цянь |
|
Фиг.23 |
|||||||
Наибольший интерес представляет класс C – его 8 логических операций можно назвать главным подмножеством (фиг.23). Во-первых, оно соответствует всем 4-м «мирам», то есть, при любом выборе одной из базовых областей как пустой, получающийся набор 8 логических операций можно интерпретировать как главное подмножество. Во-вторых, главное подмножество - одно из семи замкнутых подмножеств, содержащих одновременно тождественные «ложь» и «истину», и каждый из аргументов x и y (исходные высказывания в алгебре высказываний), причем - единственное из них, содержащее 8 логических операций. В-третьих, коды операций главного подмножества – это все шестнадцатиричные цифры, двоичный код которых содержит чётное число «1» и «0», поэтому оно инвариантно к любому перестановочному преобразованию. Главное подмножество - одно из 6 замкнутых подмножеств, обладающих свойством такой инвариантности и единственное среди них, содержащее 8 операций. Можно заметить, что, кроме лжи=0 и истины=F, коды операций главного подмножества – это как раз все шестнадцатиричные цифры, участвующие в перестановочном преобразованиия (фиг.14).
Из 4-х комбинаций класса C (15-18 – «миры 1-4») можно выделить комбинацию 18 («мир 4»). Для этого заметим, что в теоретико-множественной интерпретации (когда все 4 базовые области не пусты) операции главного подмножества разбиваются на две равные по численности группы: «внутренние» операции, не выводящие за пределы объединения x и y (выделены серым фоном), и «внешние» операции, выводящие за эти пределы до «границ внешнего мира». Эти группы отличаются значением старшего разряда их кода. Если соответствие триграммам устанавливается удалением верхней черты тетраграммы («мир 4»), то деление операций на внешние и внутренние коррелирует с разделением триграмм на женские и мужские: в первую группу – женская черта инь в удаляемой верхней позиции тетраграммы – входят женские триграммы (Кунь, Дуй, Ли, Сюнь), во вторую группу – мужская черта ян в удаляемой верхней позиции тетраграммы – входят
|
Ло Шу
|
||||||||||||||||||||||||||||||||||||||
|
Фиг.24 |
|||||||||||||||||||||||||||||||||||||||
мужские триграммы. Стоит отметить, что паре инь-ян соответствует пара внутреннее-внешнее. В любом другом «мире» (превращение тетраграмм в триграммы удалением 1,2 или 3-ей черты) указанной корреляции не наблюдается (в этих трех «мирах» внутренние операции соответствуют триграммам Кунь, Чжэнь, Кань, Дуй).
На фиг.24 изображены расположения триграмм и соответствующих логических операций главного подмножества в кресте Хэ Ту по Фу Си и в квадрате Ло Шу по Вэнь-вану («ложь» и «истина» заменены на инь и ян, что более соответствует китайской традиции). Мы видим, что в кресте Хэ Ту мужские триграммы и внешние операции занимают внешние клетки, а женские триграммы и внутренние операции – внутренние; соответственно, в квадрате Ло Шу первые располагаются на северо-востоке (направление рождения света), а вторые – на юго-западе.
Сопоставление триграмм и логических операций главного подмножества можно соотнести с операциями инверсии (дуй) и переворота (фань). Инверсия триграмм соответствует отрицанию логических операций главного подмножества. Этим свойством обладает также класс D, но не обладают классы A и B.
Переворот (фань) триграмм имеет определенный логический смысл: 4 симметричные триграммы, не изменяющиеся при перевороте, соответствуют 4-м операциям, не зависящим от аргумента x; 4 несимметричные триграммы образуют две пары, что соответствует двум парам операций, зависящим от x: x«xDy, x~y«ùx. В первую пару входят операции, в теоретико-множественном смысле всегда (а не только в мире 4) оставляющие в пределах дизъюнкции-объединения (xÍxÈy, xDyÍxÈy), а операции второй пары всегда включают антидизъюнкцию-дополнение объединения (x~yÊx¯y, ùxÊx¯y).
Наоборот, переворот тетраграмм, то есть, перестановочное преобразование логических операций вида u®u(ùx,ùy), имеет определенный «нумерологический» смысл. Здесь 4 операции с несимметричными кодами – это все некоммутативные операции, и они образуют две пары: ùx=Гэнь«x=Дуй и ùy=Кань«y=Ли. При традиционном сопоставлении триграмм с пятью стихиями (фиг.25) в порядке «взаимопорождения» (круг) и «взаимопреодоления» (пентаграмма), этим парам соответствуют осесимметричные пары Почва®Металл и Вода®Огонь, в то время как третья пара младших триграмм Чжэнь=x~y–Сюнь=xDy – коммутативные операции – соответствует одной стихии Дерева [3]. На фиг.26-27 изображены аналогичные круги стихий в, так называемых, «космогоническом» и «современном» порядках. Здесь триграммы каждой из двух наших пар расположены на круге друг рядом с другом.
|
|
|
|
|
Цянь=Металл, Кунь=Почва |
||
|
Фиг.25 |
Фиг.26 |
Фиг.27 |
Кроме самих замкнутых подмножеств логических операций рассматриваются также порождающие подмножества. Для любого подмножества логических операций можно построить его замыкание по операциям вида p(a,b). Порождающим подмножеством называют такое подмножество, что любая его часть имеет меньшее замыкание, чем оно само. Примером могут служить множества порождающие все 16 логических операций: дизъюнкция, x и отрицание y;
|
Порождающие подмножества главного подмножества |
|||
|
0, x, x~y
|
0-3-9 |
Кунь-Дуй-Чжэнь |
Почва-Металл-Дерево |
|
xDy, ùy |
6-A |
Сюнь-Кань |
Дерево-Вода |
|
Фиг.28 |
|||
штрих Шеффера или стрелка Пирса (вместе с x и y). Для нас важны множества порождающие главное – фиг.28. Мы наблюдаем 6 трехэлементные множества и 4 двухэлементные. Интересно, что в терминах стихий все двухэлементные множества образованы с участием Дерева и либо Воды, либо Почвы. На фиг.25 видно, что Вода порождает Дерево, а Дерево преодолевает Почву.
В настоящей работе мы сконцентрировали свое внимание исключительно на триграммах. Попытки сопоставления логических операций с гексаграммами, то есть, собственно с «Книгой Перемен», – дело будущего. Здесь можно высказать лишь несколько лежащих на поверхности идей такого сопоставления.
Одна идея заключается в том, чтобы, рассматривая гексаграмму как пару триграмм, интерпретировать ее как пару логических операций. Здесь не вполне ясно, что делать с этой парой операций. Можно было бы найти некую третью операцию, аргументами которой стала бы эта пара, и вычислить, тем самым, некое «логическое» значение гексаграммы, то есть, некую логическую операцию, которой обратно можно поставить в соответствие триграмму. Такой третьей операцией могла бы служить операция, соответствующая одна из ядерных триграмм гексаграммы (образованная позициями 234 или 345), таких третьих операций две и, значит, мы получим два триграммных значения гексаграммы. Другой вариант: в качестве третьей операции взять операцию верхней триграммы предыдущей гексаграммы или нижней триграммы следующей гексаграммы. Однако, здесь все же нужно учитывать парность гексаграмм (по принципу фань-дуй) и более естественно связывать операции с парой гексаграмм. В любом случае таким способом гексаграмме (или паре гексаграмм) будет поставлена в соответствие пара триграмм, которую можно рассматривать как гексаграмму, то есть, мы определим некоторое преобразование гексаграмм.
Другая идея заключается в том, чтобы выделить в гексаграмме тетраграмму логической операции (их будет уже все 16), а остальные две черты рассматривать как аргументы этой операции x и y. Так мы тоже получим «логическое» значение гексаграммы как «истина» или «ложь». Вариантов выделения тетраграммы и аргументов довольно много, автор попробовал лишь несколько из них, но получить сколько-нибудь интересный результат пока не удалось. Было бы интересно найти такой вариант, при котором истинностное значение гексаграммы коррелировало с ее смыслом», выраженном в названии, афоризмах и т.п.
Завершая на этом наше сопоставление триграмм и логических операций булевой алгебры, следует отметить, что описанная схема вовсе не претендует на то, чтобы служить «объяснением» триграмм или реконструкцией древнекитайской системы «символов и чисел». Разумеется, китайцам была неизвестна булева алгебра, которая и в Европе возникла гораздо позже самих логических операций как их математическая формализация. Подобные сопоставления можно рассматривать лишь как черновой материал для действительно исторических реконструкций.
С другой стороны, нельзя не отметить, что как европейская логика (в том числе ее простейшая часть, формализованная в булевой алгебре), так и китайская «нумерология» являлись универсальными методологическимм инструментами, предназначенными для того, чтобы «объяснять все». С этой точки зрения их сопоставление не только правомерно, но и необходимо. Этап зарождения и формирования такого инструмента проходили все культуры и в это время возникали самые разные системы, которые вступали во взаимодействие и конкуренцию. В Китае зарождение «нумерологии» также совпало с зарождением протологики, и протологические изыскания древнекитайских философов аналогичны изысканиям философов древней Греции. Поэтому вполне возможно, что в сложившейся системе «символов и чисел», в том числе и в системе «Книги Перемен» может быть обнаружен «логический след».
ЛИТЕРАТУРА
1) А.И. Кобзев «Китайская книга книг». Вступительная часть к Ю.К.Щуцкий, «Китайская классическая «Книга Перемен», 2-ое издание, М., «Наука», 1993.
2) А.И. Кобзев «Учение о символах и числах в китайской классической философии». М., Изд. Фирма «Восточная литература», 1994.
3) В.Е. Еремеев «Символы и числа «Книги перемен».АСМ, М.,2002