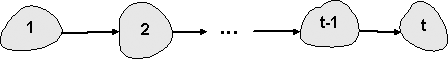Неизбыточные алгоритмы обхода ориентированных графов. Детерминированный случай.

И.Б.Бурдонов, А.С.Косачев, В.В.Кулямин

Рассматриваются проблемы тестирования программных систем, моделируемых детерминированными конечными автоматами. Необходимой, а иногда и достаточной, частью такого тестирования является обход графа состояний автомата. Основное внимание уделяется, так называемым, неизбыточным алгоритмам обхода, которым не требуется заранее заданной полной структуры графа («обход неизвестного графа» или «on-line алгоритмы»).

1.    Введение

Задача обхода графа, то есть, построения маршрута, проходящего по всем ребрам графа, хорошо известна. Ее специальным случаем является задача китайского почтальона [6,7,27], в которой обход должен иметь минимальную длину или минимальный вес для графа с заданными весами дуг. Для ориентированного графа задача усложняется, поскольку маршрут должен проходить каждое ориентированное ребро (дугу) только в направлении его ориентации.

В большинстве работ предполагается, что граф задан явно до построения его обхода [17,19]. Более сложным является случай, когда до начала работы о графе ничего неизвестно и мы получаем информацию об устройстве графа в процессе его обхода [20,24,25]. Это известная задача обхода лабиринта [10] человеком или устройством, находящимся внутри него и не имеющим плана лабиринта. Дуге графа соответствует коридор лабиринта, а вершине – перекресток. Находясь на перекрестке, мы видим выходящие из него коридоры, но мы не знаем, куда ведет тот или иной коридор, до тех пор, пока не прошли по нему до следующего перекрестка. Для выполнения нашей задачи мы, во-первых, имеем некоторую внутреннюю память (блокнот в руках человека), куда можем записывать полученную информацию о пройденной части лабиринта, и, во-вторых, делать пометки в пройденных перекрестках и коридорах. Ориентированному графу соответствует лабиринт, в котором каждый коридор закрыт с обеих сторон дверями: входная дверь открывается только с перекрестка, а выходная – только изнутри коридора, что разрешает двигаться по каждому коридору только в одном направлении.

Алгоритм, работающий на таком не заданном заранее графе, будем называть неизбыточным алгоритмом. Такие алгоритмы называются в литературе также online-алгоритмами. Его частным случаем, когда внутренняя память ограничена конечным числом состояний, является робот (конечный автомат) на графе как разновидность машины Тьюринга [3,5,8,9,12,18,24,28]. Вместо ленты у нас есть граф, ячейке ленты соответствует вершина графа, а движение влево или вправо заменяется на переход по одной из дуг, выходящих из текущей вершины графа. (Чтобы автомат робота был конечным, граф должен иметь ограничение сверху на полустепень выхода вершины – число выходящих дуг. Это ограничение можно снять, если каждой дуге также поставить в соответствие ячейку и ячейки всех дуг с общим началом связать в цикл.)

В последнее время задача обхода ориентированных графов стала особенно актуальной в связи с тестированием конечных автоматов, точнее, объектов, рассматриваемых как конечные автоматы. Написано довольно много работ о тестировании конечных автоматов. Например, обстоятельный обзор таких работ представлен в статьях  Lee и Yannakakis [15] и Bochmann и Petrenko [13].

Автомат определяется множеством своих состояний и переходов. Переход автомата – это четверка (v,x,y,v`), где v – пресостояние, x – стимул, y – реакция, v` – постсостояние. Обычно автомат задается графом состояний, вершины которого – состояния, а дуги – переходы. Автомат (граф состояний) всюду определен, если в каждом состоянии v допустим каждый стимул x, то есть, существует хотя бы один переход вида (v,x,y,v`). В противном случае, автомат частично определен. Автомат (граф состояний) детерминирован, если пресостояние и стимул однозначно определяют реакцию и постсостояние. В настоящей статье мы ограничимся рассмотрением только детерминированных частично определенных автоматов, а недетерминированный случай рассмотрим в следующей статье.

Если граф состояний автомата известен, то обычно интересуются вопросами, удовлетворяет ли он тем или иным требованиям. Эти задачи решаются аналитическими методами и о тестировании обычно речь не идет. Тестирование нужно тогда, когда граф состояний автомата неизвестен. Автомат рассматривается как «черный ящик»: мы можем подавать на автомат стимулы и получать ответную информацию о выполненном переходе, то есть, в общем случае, о реакции и постсостоянии. Задачей тестирования является проверка того, что тестируемый автомат удовлетворяет заранее заданным спецификационным требованиям. Это тестирование соответствия (conformance testing) в широком смысле. В общем случае спецификация не подразумевает проверки каждого перехода автомата. Если, например, мы хотим проверить, что число состояний автомата не меньше заданного, то тестирование прекращается, как только мы в этом убедимся, и оставшиеся непроверенными переходы нас не интересуют. Однако, такие требования являются скорее исключением, чем правилом. Обычно нас интересует полная функциональность автомата, и нам требуется проверка каждого его перехода. Такое тестирование опирается на следующие предположения.

Изменение состояния. Состояние меняется только в результате тестового воздействия, то есть, подачи стимула на автомат. С одной стороны, это означает, что автомат находится под исключительным управлением теста и никто «не мешает» тестированию, точнее, такое постороннее воздействие не изменяет наблюдаемую функциональность автомата. (Информацию о тестировании при наличии таких «помех» можно найти в работах по тестированию «серым ящиком» или «полууправляемому» тестированию [14,23].)  С другой стороны, это означает, что у теста нет других средств изменить состояние автомата. Если бы множество состояний было известно (неизвестны только переходы) и имелась возможность произвольно менять состояние с помощью прямой записи или специальной (нетестируемой) операции, задача перебора всех переходов автомата стала бы тривиальной. Априорное знание о множестве состояний реализации – сильное требование; обычно мы узнаем о нем только в процессе тестирования и только «поэлементно», то есть, о существовании состояния мы узнаем только после перехода в него.

Допустимость стимулов. В каждый момент времени мы можем тем или иным способом узнать, какие стимулы можно подавать на автомат. Понятно, что в противном случае ни о каком тестировании не может идти речь. Заметим, что во многих работах [15] эта проблема обходится предположением, что автомат всюду определен, то есть, во всех состояниях допустимы все стимулы из его алфавита стимулов. Следует также отметить, что на практике нам важна допустимость только «интересующих» нас стимулов, по которым проводится тестирование, то есть, стимулов, определенных в модели. Если в реализации допустимы какие-то другие стимулы, то это не влияет на тестирование. Фактически, это означает, что для реализации R и модели M тестируется подавтомат R(M)ÍR, определяемый переходами по модельным стимулам и состояниями, достижимыми из начального по таким переходам.

Наблюдаемость реакций. После подачи стимула на автомат мы может наблюдать выдаваемую им реакцию. Собственно говоря, при тестировании мы проверяем как раз эту реакцию. В противном случае, автомат совершал бы какие-то переходы, но мы не смогли бы узнать, правильные они или нет. С другой стороны, о правильности переходов можно судить также по постсостояниям при условии, что они наблюдаемы.

Отдельно стоит вопрос о наблюдаемости состояний автомата. Если в любой момент времени мы можем узнать состояние автомата, прочитав его или получив в ответ на специальную операцию status message (предполагается, что операция не изменяет состояние) [15], то такое тестирование будем называть тестированием с открытым состоянием. В противном случае, будем говорить о тестировании со скрытым состоянием.

Специальный случай тестирования соответствия (в узком смысле), когда спецификация – это модельный автомат, эксплицитно заданный своим графом состояний, и проверяется эквивалентность реализационного (тестируемого) автомата модельному [15]. Два состояния (одного или разных автоматов) эквивалентны, если любая последовательность стимулов, допустимая, начиная с одного состояния, допустима, начиная с другого состояния, и вызывает одну и ту же последовательность реакций. Автоматы эквивалентны, если каждому состоянию одного автомата соответствует эквивалентное ему состояние другого автомата. Модельный автомат, тем самым, описывает класс эквивалентных ему реализационных автоматов.

При наличии модельного автомата тестирование с открытым состоянием сводится к обходу модельного графа [15], при котором каждый модельный переход сопровождается подачей на реализационный автомат того же стимула и проверкой того, что получаемые реализационные реакция и постсостояние такие же, как в модельном переходе. Заметим, что в такой постановке задачи, поскольку модельный граф известен, не требуется неизбыточности алгоритма обхода. Если реализационное состояние нам недоступно (тестирование со скрытым состоянием), приходится вводить специальные ограничения на реализацию и модель и прибегать к гораздо более сложным методам проверяющих последовательностей (checking sequence) [15]. Обход модельного графа в этом случае недостаточен, но, очевидно, также необходим, и также для этого не требуется неизбыточности алгоритма обхода.

К сожалению, на практике спецификации, во-первых, не описывают явно модельный автомат и существует проблема его эксплицирования, а, во-вторых, реализация должна быть эквивалентна не полному модельному автомату, а некоторому его подавтомату, заранее неизвестному.

Наиболее широко распространенный случай – это имплицитные спецификации в виде пред- и постусловий. Предусловие –  предикат над пресостоянием и стимулом – определяет допустимость стимулов в состояниях, а постусловие – предикат над пресостоянием, стимулом, реакцией и постсостоянием – определяет возможные переходы. Эксплицирование автомата из таких спецификаций сводится к решению системы уравнений общего вида и, в общем случае, не имеет удовлетворительного решения. Но дело не только в этом.

Обычно считается, что спецификация описывает возможные, но не обязательные, переходы автомата. Если спецификация допускает несколько переходов по данному стимулу из данного пресостояния, то это не обязательно означает недетерминизм реализации. Допускается, чтобы реализация имела хотя бы один из таких переходов, но не обязательно все; детерминированная реализация должна иметь ровно один такой переход. Фактически, это означает, что модельному автомату соответствует не один класс эквивалентных реализационных автоматов, а семейство таких классов. Реализационный автомат, точнее, как сказано выше, его подавтомат R(M)ÍR, определяемый модельными стимулами, эквивалентен некоторому подавтомату M(R) спецификационного автомата M, причем в каждом состоянии M(R) допустимы все стимулы, которые в этом состоянии допустимы в M, но среди всех переходов в M из данного состояния по данному стимулу не все должны присутствовать в M(R). (Иногда в этом случае говорят о квази-эквивалентности R и M(R) и редукции R к M [13].)  Понятно, что в этом случае, во-первых, работа по эксплицированию спецификационного автомата M может оказаться чрезмерной, так как нам требуется только его подавтомат M(R), число состояний и переходов которого может быть во много раз меньшим, чем в M. Во-вторых, сам M(R) заранее неизвестен, поскольку определяется не только M, но и R.

Можно также отметить, что недетерминированный спецификационный автомат M может использоваться для тестирования детерминированных реализационных автоматов R [16]. В этом случае эксплицированный подавтомат M(R) также детерминирован.  Это важно, поскольку тестирование детерминированных автоматов намного проще тестирования недетерминированных.

Таким образом, нужда в неизбыточном алгоритме обхода графа состояний возникает естественным образом. Тестирование с открытым состоянием, фактически, сводится к такому алгоритму, а для тестирования со скрытым состоянием оно необходимо (хотя и недостаточно).

В части 2 настоящей статьи формулируются основные понятия графа, обхода и алгоритма. В части 3 изучается проблема существования и длины обхода графов. В части 4 предлагаются неизбыточные алгоритмы обхода. В части 5 описывается применение этих алгоритмов в тестировании.

2.    Понятия графа и алгоритма движения по графу

Ориентированным графом (далее просто графом) G будем называть совокупность трёх объектов: VG – множество вершин, XG – множество стимулов, EGÍVG´XG´VG – множество дуг.

Стимул x допустим в вершине a, если в графе существует дуга (a,x,b). Для дуги (a,x,b) вершину a будем называть началом дуги, вершину b – концом дуги, стимул x – раскраской дуги. Если стимул дуги несущественен, мы будем также вместо (a,x,b) писать просто (a,b).

Замечание: При тестировании граф рассматривается как граф состояний автомата. Однако, при изучении алгоритмов обхода мы не используем раскраску дуг графа реакциями, поскольку для алгоритма достаточно при проходе любой дуги уметь определять конец дуги (постсостояние), начинающейся в данной вершине (пресостоянии), и раскрашенной данным стимулом. При тестировании с открытым состоянием мы определяем постсостояние непосредственно, а при тестировании со скрытым состоянием постсостояние иногда можно вычислить по реакции, но мы относим это к способу определения постсостояния, внешнему для алгоритма обхода, а не к самому алгоритму обхода. Подробнее о реакции в процессе тестирования см. раздел 5.

Граф называется конечным, если множества вершин и дуг конечны. Число вершин и дуг конечного графа обозначим, соответственно, n и k.

Граф называется детерминированным, если конец дуги однозначно определяется ее началом и допустимым в нем стимулом: для дуг (a,x,b) и (a`,x`,b`) из a=a` и x=x` следует b=b`. В данной статье мы будем рассматривать только конечные детерминированные графы.

Дуги (a,b) и (a`,b`) называются смежными, если конец первой дуги совпадает с началом второй дуги: b=a`. Маршрутом P длины n в графе G называется последовательность n смежных дуг: для i=1..n–1 дуга P[i] смежна с дугой P[i+1]. Начало a первой дуги маршрута будем называть его началом, конец b последней дуги маршрута – его концом, сам маршрут – [a,b]-маршрутом. Пустой последовательности дуг соответствует маршрут нулевой длины, начало и конец которого совпадают. Маршрут будем называть обходом, если он содержит все дуги графа.

Алгоритмом движения по графу будем называть алгоритм, который в процессе своей работы строит маршрут в графе. Формально такой алгоритм можно определить как специальный вид машины с абстрактным состоянием (машина Гуревича, ASM – Abstract State Machine [26]), в котором внешние операции частично специфицированы заданием графа, на котором происходит работа алгоритма, и текущей вершины в нем. Для наших целей достаточно указать, что алгоритму предоставляются две специальные внешние операции status(), возвращающая идентификатор текущей вершины, и call(x), которая осуществляет переход из текущей вершины a по дуге со стимулом x. Для детерминированного графа такая дуга (a,x,b) единственная (единственна вершина b). Предусловием операции call(x) является допустимость стимула x в текущей вершине a. Маршрут строится алгоритмом как последовательность дуг, проходимых последовательными вызовами операции call. Следует отметить, что никакая внешняя операция (не говоря уже о внутренней) не меняет сам граф, и единственной модифицирующей операцией, которая может изменить текущую вершину, является операция call.

Неизбыточным алгоритмом будем называть алгоритм движения по графу, который зависит только от пройденной части графа и допустимости стимулов в текущей вершине. Допустимость стимулов алгоритм может определить с помощью специальной внешней операции next(), которая возвращает стимул, неспецифицированным образом выбираемый среди не выбранных ранее стимулов, допустимых в текущей вершине, осуществляя тем самым итерацию стимулов в вершине. Если все стимулы, допустимые в текущей вершине, уже выбирались, будем считать, что next() возвращает «пустой» символ e.

Свободным алгоритмом  будем называть неизбыточный алгоритм, который узнает о допустимости стимула, еще не опробованного в текущей вершине a, не заранее, а одновременно с проходом по дуге, раскрашенной этим стимулом. Иначе говоря, свободный алгоритм осуществляет первичный проход по любой еще не пройденной дуге с началом в текущей вершине, используя совмещенную внешнюю операцию nextcall(): x=next(); if x¹e then call(x); return x else return e end. Эта операция неспецифицированным образом выбирает еще не опробованный в текущей вершине a стимул x и проходит по дуге (a,x,b). Если все стимулы уже опробованы в текущей вершине, возвращается пустой символ e. Для вторичного прохода по дуге (a,x,b), по-прежнему, используется операция call(x) в тот момент, когда текущей вершиной является вершина a.

Алгоритм предназначен для решения той или иной задачи; в данной статье такой задачей является обход графа. Нас будут интересовать только такие алгоритмы, которые останавливаются через конечное число шагов. В момент остановки алгоритм может сообщить, выполнен обход или нет. Возможен также случай, когда построенный маршрут является обходом, но алгоритм об этом «не знает». Противоположный случай, когда обход не выполнен и алгоритм «знает», что в данном графе вообще нет обхода. Подобную информацию, сообщаемую алгоритмом в момент остановки, будем называть вердиктом алгоритма. Мы будем говорить, что вердикт достоверен, если сообщаемая в нем информация соответствует действительности.

Работа алгоритма, вообще говоря, зависит от выполнения внешних операций; для неизбыточных алгоритмов – от операции next, которая определена неоднозначно. Будем говорить, что алгоритм совершает гарантированный обход данного графа с данной начальной вершиной, если это происходит при любом допустимом выполнении всех внешних операций; для неизбыточных алгоритмов – независимо от итерации стимулов в вершинах (next).

3.    Обход графа

3.1. Сильно-связные графы

Вершина b достижима из вершины a, если существует [a,b]-маршрут. Граф сильно-связен, если из каждой его вершины достижима каждая его вершина. Путем называют маршрут без повторного вхождения вершин.

Теорема 3.1: 1) Для любого сильно-связного графа и любой пары его вершин a и b всегда существует [a,b]-обход с длиной O(nk). 2) Для любых n и k существует сильно-связный граф с числом вершин n и числом дуг k`³k, в котором любой обход имеет длину W(nk`).

1) Произвольным образом линейно упорядочим все дуги графа так, чтобы первая дуга начиналась в вершине a, а последняя дуга заканчивалась в вершине b. Для двух последовательных дуг (v_i,v_i`) и (v<sub>i+1</sub>,v<sub>i+1</sub>`) в сильно-связном графе всегда существует маршрут из конца v_i` i-ой дуги в начало i+1-ой дуги v<sub>i+1</sub>. Удаляя из него циклы, получаем, путь P<sub>i</sub>,  ведущий из v<sub>i</sub>` в v_i+1. Искомый обход представляет собой конкатенацию дуг и путей: (v₁,v₁`)^P<sub>1</sub>^…^(v<sub>i</sub>,v<sub>i</sub>`)^P_i^…^P_k–1^(v_k,v_k`), где v₁=a и v_k=b. 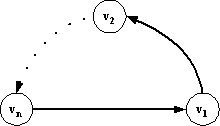Поскольку длина пути в графе не превосходит n–1, обход имеет длину не более k+(n–1)(k–1)=n(k–1)+1, то есть, O(nk).

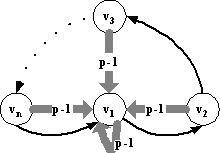
2) Пример графа приведен на рис.1, где p=k`/n – полустепень выхода каждой вершины.

Обход этого графа можно представить в виде конкатенации маршрутов P₁,…,P_t, причем каждый из P₁,…,P_t-1 заканчивается дугой (v_i,v₁), где i>1, а каждый из P₂,…,P_t-1 начинается в v₁. Каждый маршрут из P₂,…,P_t-1, заканчивающийся дугой (v_i,v₁) имеет длину i, а их число равно p-1. Поэтому, считая, что маршрут P₁ заканчивается дугой (v_j,v₁) и имеет длину не менее 1, и не учитывая последний маршрут P_t, получаем нижнюю оценку длины обхода
(p–1)+2(p–1)+…+n(p–1)–j+1 = (p–1)n(n–1)/2 –j+1 ³ (p–1)n(n–1)/2–n+1 = L. Нам достаточно, чтобы для некоторой константы C>0 при любом n>0 выполнялось L ³ Cpn² = Ck`n. Легко показать, например, что это так для C=1/3 и p³3. Тем самым, мы определяем k` = max{k,3n}.

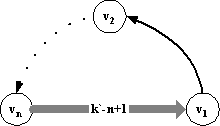
Заметим, что в примере на рис.1 полустепени выхода у всех вершин одинаковые. Это сделано для того, чтобы не накладывать на число стимулов ограничений снизу, кроме необходимого k`/n. Без этого требования пример можно упростить, заменив все дуги, ведущие из v<sub>i</sub> в v<sub>1</sub> на дуги, ведущие из v<sub>n</sub> в v<sub>1</sub>, что требует k`–n+1 стимулов (рис.2). ÿ

3.2. Достижимые графы

Поскольку взаимная достижимость вершин – это отношение эквивалентности, в общем случае граф G разбивается на компоненты сильной связности, на множестве которых достижимость является отношением частичного порядка. Компонент является подграфом графа G,  множество вершин которого – это класс эквивалентности, а дуги – все дуги графа G, начало и конец которых принадлежат этому классу. Компонент, которому принадлежит вершина a, будем обозначать K(a). Дугу графа G, начало и конец которой относятся к разным компонентам, будем называть связующей.

Для графа G его фактор-графом по отношению взаимной достижимости будем называть граф F(G), вершинами которого являются компоненты сильной связности графа G, а дуга (A,x,B), где A¹B – компоненты графа G, существует тогда и только тогда, когда в графе G существует связующая дуга (a,x,b), где aÎVA и bÎVB. Вершины фактор-графа будем называть фактор-вершинами, а дуги – фактор-дугами.

 Достижимым графом называется граф, все вершины которого достижимы из выделенной начальной вершины. В дальнейшем, специально не оговаривая это, мы будем рассматривать только достижимые графы, поскольку только в них, очевидно, возможен обход.  Граф называется ациклическим, если в нем нет циклических маршрутов; источником называется вершина, в которую не входят дуги; стоком называется вершина, из которой не выходят дуги.

Теорема 3.2: Для того, чтобы граф G был достижимым графом с начальной вершиной v₀, необходимо и достаточно, чтобы его фактор-граф F(G) был ациклическим графом с одним источником K(v₀).

Необходимость. Фактор-граф F(G), очевидно, является ациклическим. В достижимом графе G для любой вершины v существует [v₀,v]-маршрут. Оставляя в нем только связующие дуги и заменяя их соответствующими фактор-дугами, получаем [K(v₀),K(v)]-маршрут в фактор-графе, то есть, F(G) также является достижимым графом и следовательно, имеет только один источник K(v₀).

Достаточность. В ациклическом фактор-графе F(G) с одним источником K(v₀) для каждой вершины v существует [K(v₀),K(v)]-маршрут как последовательность фактор-дуг, соответствующих связующим дугам (a_i,b_i), i=1..t. Обозначая b₀=v₀ и a_t+1=v, получаем, что для i=0..t, вершины b_i и a_i+1 принадлежат одному компоненту и, следовательно, в графе G существует [b_i,a_i+1]-маршрут P_i. [v₀,v]-маршрут в графе G строится как конкатенация P₀^(a₁,b₁)^…^P_t–1^(a_t,b_t)^P_t. ÿ

3.3. Графы 1-го рода

Графом 1-го рода будем называть граф с линейным порядком достижимости компонентов, в котором из каждого непоследнего компонента выходит только одна связующая дуга и она ведет в следующий компонент. По умолчанию, начальная вершина v₀ принадлежит первому компоненту. Иными словами, фактор-граф такого графа состоит из одного ациклического маршрута с началом в компоненте начальной вершины K(v₀) (рис.3).

Рис.3

Пройденным графом маршрута будем называть подграф, состоящий из дуг маршрута и инцидентных им вершин.

Теорема 3.3: 1) Пройденный граф маршрута является графом 1-го рода, начало и конец маршрута принадлежат, соответственно, его первому и последнему компонентам. 2) [a,b]-обход существует для и только для графа 1-го рода, в котором вершины a и b принадлежат, соответственно, первому и последнему компонентам; минимальная длина обхода равна O(nk). 3)  Для любых возможных n и k существует граф 1-го рода с n вершинами и k`³k дугами, любой обход которого имеет длину W(nk`). 4) Обход из любой начальной вершины v₀ существует для и только для сильно-связных графов.

Утверждение 1) непосредственно следует из того, что все вершины пройденного графа линейно упорядочиваются маршрутом в порядке достижимости. 2) Из 1) следует существование обхода только для графов 1-го рода. Обратно, для графа 1-го рода со связующими дугами (a_i,b_i), i=1..t–1, обозначая b₀=a и a_t=b,  строим [b_i–1,a_i]-обход P_i i-го компонента для i=1..t и [a,b]-обход графа как конкатенацию P₁^(a₁,b₁)^…^P_t–1^(a_t,b_t)^P_t. Длина этого обхода не превосходит t–1+S{O(n_ik_i)|i=1..t}, где n_i, k_i – число вершин и дуг i-го компонента, то есть, равна O(nk). Утверждение 3) доказано в Теореме 3.1 для сильно-связных графов (t=1). Утверждение 4) непосредственно следует из утверждения 2). ÿ

3.4. Покрытия достижимых графов

Множество маршрутов, начинающихся в начальной вершине v₀, будем называть покрытием  графа, если каждая вершина и каждая дуга графа входит хотя бы в один из этих маршрутов. Длиной покрытия будем называть сумму длин его маршрутов.

Теорема 3.4: Покрытие существует для и только для достижимых графов и его минимальная длина равна O(nk); для любых возможных n и k существует граф достижимости с n вершинами и k`³k дугами, любое покрытие которого имеет длину W(nk`).

Утверждение теоремы о существовании покрытия непосредственно следует из определения достижимого графа G с начальной вершиной v₀: для каждой вершины a имеется [v₀,a]-маршрут P(a), для каждой дуги (a,b) имеется маршрут P(a)^(a,b), проходящий через эту дугу.

Для оценки длины покрытия рассмотрим фактор-граф F(G), который, по Теореме 3.2, является ациклическим графом с одним источником K(v₀). Обозначим  t – число компонентов, а k₀ – число связующих дуг графа G. Выделим в F(G) остов (максимальное дерево), ориентированный от корневого компонента-источника K(v₀); в нем t–1 дуг, остальные k₀–(t–1) связующие дуги – хорды. Для покрытия F(G) достаточно взять a) все фактор-маршруты, ведущие из корня K(v₀) в листовые компоненты, из которых не выходят хорды, и дополнительно b) все фактор-маршруты, ведущие из корня в начальные компоненты всех хорд и далее проходящие по хорде. Число фактор-маршрутов a) не превосходит t, число фактор-маршрутов b) не превосходит k₀–(t–1); суммарное число фактор-маршрутов – не более k₀+1.

Каждый такой фактор-маршрут F можно рассматривать как чередующуюся последовательность компонентов и связующих дуг. Заменим каждое вхождение компонента K в фактор-маршрут F маршрутом P(K,F) в графе G, который начинается в конце связующей дуги фактор-маршрута F, входящей в K (для первого компонента K(v₀) – в вершине v₀), и заканчивается в начале связующей дуги фактор-маршрута F,  выходящей из K (для последнего компонента – в любой его вершине). В результате получим маршрут P(F) в графе G как чередующуюся конкатенацию маршрутов P(K,F) и связующих дуг. Для каждого компонента K в одном из маршрутов P(F), проходящих через K, маршрут P(K,F) выберем обходом компонента K, а во всех остальных – либо путем, если K непоследний компонент в F, либо маршрутом нулевой длины, если K – последний компонент в F. Очевидно, это множество маршрутов P(F) будет покрытием графа G. Если бы каждый маршрут P(F) содержал не обходы, а только пути в компонентах, он сам был бы путем или путем, удлиненным на одну дугу (хорду фактор-графа), и, следовательно, его длина не превосходила бы n, а сумма длин – (k₀+1)n. Поскольку каждый i-ый компонент обходится ровно в одном маршруте P(F), длина покрытия не превосходит (k₀+1)n+S{O(n_ik_i)|i=1.. t}, где n_i, k_i – число вершин и дуг i-го компонента, то есть, равна O(nk).

Оценка W(nk`) достигается на графе на рис.1,2 с начальной вершиной v₁. ÿ

4.    Алгоритмы обхода

4.1. Графы 2-го рода и свободные алгоритмы

Для маршрута в графе вершину будем называть полностью пройденной, если в этом маршруте пройдены все выходящие из вершины дуги.

Графом 2-го рода будем называть такой граф 1-го рода, в котором все компоненты, кроме, быть может, последнего, состоят из одной вершины и не содержат дуг, кроме одной связующей дуги, ведущей в следующий компонент (рис.4).

Рис.4

Теорема 4.1: 1) Любой свободный алгоритм может гарантированно обойти только граф 2-го рода с начальной вершиной v₀ из первого компонента и остановкой в вершине из последнего компонента. 2) Существует свободный алгоритм A₁, который останавливается на любом графе, проходя маршрут длиной O(nk), и гарантированно обходит все графы 2-го рода  с начальной вершиной v₀ из первого компонента.

1) По Теореме 3.3, обход существует только для графа 1-го рода. Если граф не 2-го рода, то некоторый непоследний компонент графа либо состоит более, чем из одной вершины, либо из его единственной вершины выходит не только связующая дуга. В первом случае, в силу сильной связности компонента, имеется маршрут из начала связующей дуги в другую вершину компонента, следовательно, из начала связующей дуги (a,x,b) выходит еще одна дуга (a,x`,b`), а во втором случае наличие таких двух дуг явно постулируется. Когда алгоритм впервые оказывается в вершине a, в ней еще ни один стимул не опробован, и поэтому свободный алгоритм должен применить операцию nextcall. Поскольку алгоритм должен гарантированно обходить граф, то есть, независимо от выполнения этой операции, предположим, что она выбирает стимул x. В этом случае мы пройдем по связующей дуге (a,x,b) в следующий компонент и, следовательно, больше не сможем вернуться в вершину a, и дуга (a,x`,b`) останется непройденной.

2) В процессе работы алгоритма A₁ мы будем хранить описание пройденного графа, запоминая все пройденные дуги. Кроме того, будем помечать вершины, в которых операция nextcall вернула пустой символ e, то есть, вершины, которые гарантированно полностью пройдены. Заметим, что вершина может быть полностью пройдена, но мы об этом еще не знаем и она непомечена.

Шаг алгоритма состоит из следующих пунктов:

1.      Выполняем операцию nextcall, запоминая пройденные дуги (стимул дуги возвращается nextcall, а ее конец определяется с помощью операции status), до тех пор, пока nextcall не вернет пустой символ e. В последнем случае помечаем текущую вершину.

2.      Если все пройденные вершины помечены (и, тем самым, полностью пройдены), алгоритм останавливается.

3.      В противном случае, в пройденном графе ищем путь  из текущей вершины в какую-нибудь непомеченную вершину. Если такой путь есть, проходим его с помощью операций call. Шаг заканчивается.

4.      Если такого пути нет, алгоритм останавливается.

Остановка алгоритма. Каждый из этих пунктов выполняется за конечное время, поскольку в графе конечное число дуг (конечность п.1) и конечное число путей (конечность п.3). За один шаг из пунктов 1–3 алгоритм проходит хотя бы одну непройденную дугу и/или помечает хотя бы одну непомеченную вершину. Поэтому алгоритм A₁ останавливается через конечное время на любом графе.

Длина маршрута. Пройденный маршрут можно представить как конкатенацию первичных вхождений дуг (п.1) и соединяющих их путей (п.3), поэтому длина маршрута получается O(nk).

Гарантированный обход. В графе 2-го рода каждый непоследний компонент состоит из одной вершины, из которой выходит одна дуга, ведущая в следующий компонент, поэтому алгоритм, начинающий работать в вершине первого компонента, очевидно, после п.1 окажется в последнем компоненте и, следовательно, остановится в некоторой вершине b последнего компонента. Пусть в момент остановки имеется непройденная дуга (c,d), тогда ее начало c не помечено и, очевидно, принадлежит последнему компоненту. Тогда существует маршрут из b в c. Удаляя из маршрута циклы, получаем путь из текущей вершины b в непомеченную вершину c. Если этот путь содержит только пройденные дуги, то алгоритм не должен был остановиться (п.3). Если же на этом пути есть непройденные дуги, то рассмотрим начальный отрезок этого пути до первой непройденной дуги (c`,d`) – вершина c` непомечена и в пройденном графе имеется путь в нее из текущей вершины, следовательно алгоритм не должен был остановиться (п.3). Мы пришли к противоречию и, значит, в момент остановки все дуги пройдены и совершен обход. ÿ

Различные алгоритмы, использующие стратегию алгоритма A₁, различаются выбором непомеченной вершины v` из текущей помеченной вершины v в п.3 [25]. Алгоритмы, основанные на обходе остова графа, выбирают самую дальнюю от корня («поиск в глубину») или самую ближнюю к корню («поиск в ширину») вершину v`, достижимую из v. «Жадный» алгоритм выбирает v` ближайшую к v по длине [v,v`]-пути.

Теперь исследуем вопрос: какие достоверные вердикты может выносить свободный алгоритм обхода?

Об отсутствии непройденной дуги, выходящей из данной вершины, свободный алгоритм может узнать, только получив пустой стимул в ответ на операцию nextcall, когда эта вершина была текущей. Такую вершину назовем помеченной, как это делается в алгоритме A₁. Если в момент остановки алгоритма отсутствуют непомеченные вершины, алгоритм может вынести достоверный вердикт «совершен обход» (напомним, что мы рассматриваем только достижимые графы). Это может произойти только в сильно-связном графе, поскольку проход по связующей дуге делает невозможным возвращение в ее начальную вершину v₀ и, следовательно, эта вершина останется непомеченной. Поэтому, если все пройденные вершины помечены, достоверным будет даже более сильный вердикт «совершен гарантированный обход». Алгоритм A₁ может делать это в п.2. Если же в момент остановки остались непомеченные вершины (п.4 алгоритма A₁), алгоритм, анализируя пройденный граф, может вынести один из двух достоверных вердиктов: если пройденный граф 2-го рода – «неизвестно, совершен ли обход, но если совершен, то обход гарантированный»; в противном случае – «неизвестно, совершен ли обход, но если совершен, то обход негарантированный».

4.2. Неизбыточные алгоритмы

Неизбыточные алгоритмы отличаются от свободных тем, что могут получить с помощью операции next опережающую информацию о стимулах непройденных дуг до того, как они будут пройдены. Это дает возможность неизбыточным алгоритмам отождествить понятия помеченной и полностью пройденной вершины и, следовательно, выносить более сильные достоверные вердикты.

Теорема 4.2: Существует неизбыточный алгоритм A₂, который останавливается на любом графе, проходя маршрут длиной O(nk), и выносит достоверный вердикт 1) «совершен гарантированный обход» для всех графов 2-го рода, 2) «совершен негарантированный обход» при некоторых выполнениях внешних операций для графов 1-го (но не 2-го) рода, и 3) «обход не совершен» при некоторых выполнениях внешних операций для графов 1-го (но не 2-го) рода, и для всех графов не 1-го рода.

Алгоритм A₂ является модификацией алгоритма A₁ и строит тот же самый маршрут. Вместо операции nextcall применяется «опережающая» операция next, результат которой запоминается в текущей вершине (при первом попадании в вершину next выполняется два раза подряд, если, конечно, из вершины выходит хотя бы одна дуга). После этого по непройденной дуге мы идем операцией call(x), где x – стимул, выданный в текущей вершине предпоследней операцией next. За счет этого алгоритм помечает вершину непосредственно перед тем, как выходит из нее по последней непройденной дуге. Тем самым, понятия помеченной и полностью пройденной вершины совпадают. При остановке в п.2 (все вершины помечены) алгоритм анализирует пройденный граф. Если это граф 2-го рода, выносится вердикт «совершен гарантированный обход», в противном случае – «совершен негарантированный обход». В п.4 выносится вердикт «обход не совершен». ÿ

4.3. Предикат связующих дуг

Алгоритм может гарантированно обходить графы 1-го рода, если ему каким-то внешним образом поставляется информация о связующих дугах. Пусть в каждой вершине графа задан предикат от стимула p(x), который будем называть предикатом связующих дуг.  Предикат достоверен, если он истинен на и только на стимулах связующих дуг. Алгоритм, с внешними операциями next, call и p, конечно, не является неизбыточным, но в некотором смысле «минимально избыточным» алгоритмом.

Теорема 4.3: Существует алгоритм A₃ с предикатом связующих дуг p, который останавливается на любом графе, проходя маршрут длиной O(nk), и гарантированно обходит графы 2-го рода и графы 1-го рода с достоверным предикатом.

Алгоритм A₃ отличается от алгоритма A₂ тем, что сначала проходятся только несвязующие дуги, выходящие из пройденных вершин, а стимулы связующих дуг запоминаются в их начальных вершинах. Когда несвязующих непройденных дуг больше не остается, алгоритм ищет в пройденном графе путь в начало одной из запомненных непройденных связующих дуг и, если находит такой путь, проходит его и связующую дугу, после чего снова ищет непройденные несвязующие дуги. Является дуга связующей или нет, определяется по предикату p. Доказательство утверждений теоремы об остановке алгоритма, длине маршрута и обходе очевидно. ÿ

Легко показать, что алгоритм A₃ после остановки может проанализировать пройденный граф и выдать один из следующих достоверных вердиктов:

1.      «Совершен обход», если из пройденных вершин не выходят непройденные дуги.

a)      + «Обход гарантированный и предикат достоверен», если предикат в пройденном графе 1-го рода истинен на и только на его связующих дугах.

b)      + «Обход гарантированный, но предикат недостоверен», если предикат в пройденном графе 1-го рода истинен на некоторых дугах последнего компонента и/или ложен на некоторых связующих дугах, из начала которых не выходят другие дуги.

c)      + «Обход негарантированный и предикат недостоверен» – во всех остальных случаях.

2.      «Обход не совершен», если хотя бы из одной пройденной вершины выходит непройденная дуга.

a)      + «Либо предикат достоверен и тогда исходный граф не 1-го рода, либо предикат недостоверен и тогда неизвестно, является ли исходный граф графом 1-го рода», если предикат истинен на и только на связующих дугах и непройденных дугах.

b)      + «Предикат не достоверен и неизвестно, является ли исходный граф графом 1-го рода» – во всех остальных случаях.

Предикат p формально определен на тройках (граф, вершина, стимул). Будем называть предикат неизбыточным, если он не зависит от графа. Более точно, зависимость предиката от графа сводится к зависимости от множества стимулов, допустимых в вершине, то есть, формально предикат определен на тройках (вершина, множество допустимых в вершине стимулов, стимул). Если неизбыточный предикат рассматривать не как внешнюю, а как внутренную операцию алгоритма, то соответствующим образом модифицированный алгоритм A₃ (обозначим его A₄), во-первых, будет неизбыточным, и во-вторых, гарантированно обходит все графы 2-го рода и те графы 1-го рода, на которых предикат достоверен.

Вместе с тем, неизбыточный предикат, очевидно, не может быть достоверен на всех графах с выделенными начальными вершинами v₀, изоморфных с точностью до раскраски дуг стимулами, если это не графы 2-го рода.

Теорема 4.4: Не существует неизбыточного алгоритма, который обходил бы некоторый граф G 1-го (но не 2-го) рода и все графы, отличающиеся от G только раскраской дуг стимулами.

Доказательство похоже на доказательство утверждения 1) Теоремы 4.1. Если граф G не 2-го рода, то в нем имеется связующая дуга (a,x,b), из начала которой выходит еще одна дуга (a,x`,b`). Рассмотрим момент времени, когда алгоритм осуществляет первичный проход по второй дуге – в вершине a вызывается операция call(x`). Если алгоритм обходит граф, то в этот момент первая дуга  (a,x,b) еще не пройдена. Если алгоритм неизбыточен, то информация о графе, которой он обладает в этот момент, одинакова как для графа G, так и для графа G`, отличающегося от G переменой местами стимулов раскраски этих двух дуг (a,x`,b) и (a,x,b`). Поэтому в графе G` алгоритм пойдет по дуге (a,x`,b) в тот момент, когда дуга (a,x,b`) еще не пройдена. Однако, в этом графе связующей является дуга (a,x`,b), то есть, обход совершен не будет. ÿ

4.4. Оптимальный по времени и памяти свободный алгоритм

До сих пор нас интересовала только длина обхода, строящегося алгоритмом (количество операций call), но не время его работы (общее количество элементарных операций, как внешних, так и внутренних) и не объем используемой памяти.

Теорема 4.5: Существует свободный алгоритм A₅, который останавливается на любом графе, и гарантированно обходит все графы 2-го рода  с начальной вершиной v₀ из первого компонента. Время работы алгоритма O(nk), а используемая память O(n(log₂n+I+X)) бит, где I и X – размер, соответственно, идентификатора вершины и стимула в битах. При этом выносятся достоверные вердикты, возможные для свободных алгоритмов.

Идея алгоритма заключается в построении в пройденном графе forward-пути (состоит из forward-дуг) и леса back-деревьев (состоит из back-дуг). Согласно Теореме 3.3, пройденный граф является графом 1-го рода, начальная вершина v₀ принадлежит первому компоненту, а конечная вершина v – последнему. Пройденные вершины, в которых алгоритм вызывал операцию nextcall с получением в ответ пустого символа e, помечены и, тем самым, гарантированно полностью пройдены. 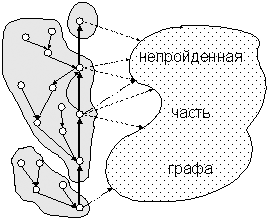Работа алгоритма представляет собой последовательность шагов, в начале каждого шага выполнены следующие условия:

Ш        forward-путь – [v₀,v]-путь, все вершины которого непомечены.

Ш        Все остальные пройденные вершины помечены.

Ш        Текущей вершиной является конец forward-пути.

Ш        Каждое back-дерево является остовом компонента сильной связности пройденного графа, ориентированным к корню, который лежит на forward-пути; этот корень будем называть также корнем компонента. (См. рис.5.)

Рис.5

Рассмотрим работу алгоритма на одном шаге. Если из текущей вершины (конца forward-пути) выходит непройденная дуга e, идем по ней. Если попадаем в новую (не пройденную ранее) вершину, forward-путь удлиняется на дугу e и шаг заканчивается. В противном случае, двигаемся по back-дугам до первой вершины, лежащей на forward-пути (в крайнем случае, мы дойдем до корня back-дерева), и далее – по forward-дугам до конца forward-пути, и заканчиваем шаг. Если дуга e вела ниже корня back-дерева последнего компонента, соответствующим образом корректируем back-деревья. Такое же движение по back-дугам и далее по forward-дугам совершаем и в том случае, когда из конца forward-пути не выходят непройденные дуги, но только теперь конец forward-пути становится помеченным и мы останавливаемся в предыдущей на forward-пути вершине и укорачиваем forward-путь на последнюю его дугу. Если такой предпоследней вершины нет (forward-путь нулевой длины), алгоритм останавливается.

Заметим, что дуги, которые в процессе работы алгоритма A₅ были forward-дугами в началах шагов, в момент остановки образуют forward-дерево – остов пройденного графа, ориентированный от корня. Фактически, алгоритм обходит это forward-дерево методом поиска в глубину.

Для оценки времени работы алгоритма опишем используемые им структуры данных:

• Для представления леса back-деревьев используется список Traversed всех пройденных вершин в произвольном порядке. Traversed-описание вершины содержит:
• идентификатор вершины,
• ссылку «вперед» по списку,
• описание back-дуги – дуги back-дерева, выходящей из этой вершины:
• стимул дуги,
• ссылка на Traversed-описание конца дуги (для корня ссылка нулевая),
• ссылку на Forward-описание непомеченной вершины (для помеченной вершины ссылка нулевая).
• Для представления forward-пути ­используется двунаправленный список Forward непомеченных пройденных вершин в порядке forward-пути. Forward-описание вершины содержит:
• ссылку на Traversed-описание,
• описание forward-дуги – дуги forward-пути, выходящей из этой вершины:
• ссылка «вперед» по списку Forward на Forward-описание конца дуги,
• стимул дуги
• ссылку «назад» по списку Forward,
• индекс компонента сильной связности, которому принадлежит вершина, в качестве которого используется индекс его корня по списку Forward.
• Длина списка Forward.

Ссылка по списку вершин и индекс компонента не превосходят n и поэтому для их хранения требуется O(log₂n) бит памяти. Поскольку число описаний не превосходит числа вершин n, общий объем используемой памяти O(n(log₂n+I+X)) бит. Эта оценка точная по порядку: в момент остановки алгоритма на графе 2-го рода список Traversed содержит n описаний, то есть, занимает W(n(log₂n+I+X)) бит.

Замечание: Внешняя операция next, вообще говоря, также занимает память для каждой вершины – последний стимул (или его номер), который она выдавала (или собирается выдавать). Эта дополнительная память, очевидно, также имеет объем O(nI) бит.

Теперь шаг алгоритма опишем подробнее:

1.      Выполняется операция nextcall.

2.      Если nextcall возвращает стимул x¹e, с помощью операции status определяем конец b дуги (a,x,b) и ищем его в списке Traversed.

3.      Если не находим – вершина b новая, то создаем Traversed- и Forward-описания вершины b, помещая их в соответствующие списки; forward-путь удлиняется на forward-дугу (a,x,b). Поскольку вершина b – корень последнего компонента K(b), индекс K(b) устанавливается равным длине списка Forward, то есть, индексу в нем Forward-описания вершины b. Шаг заканчивается.

4.      Вершина b старая. Наша задача – вернуться в вершину a, скорректировав, при необходимости, back-деревья и индексы компонентов. Если вершина b не лежит на forward-пути, то по back-дугам двигаемся с помощью операций call до первой вершины c, лежащей на forward-пути. Сравниваем индексы компонентов в вершинах a и c. Если они равны, двигаемся с помощью операций call по forward-дугам до конца forward-пути. Если они не равны, то коррекция необходима, и во время движения устанавливаем для каждой вершины после c, начиная с первого попавшегося корня (включительно) индекс компонента такой же, как в c, а в качестве back-дуги – forward-дугу, кроме конца forward-пути, где back-дугой становится дуга (a,x,b). Заметим, что в п.4 мы проходит в графе контур из двух половинок: back- и forward-пути, который всегда имеет длину не более n. Шаг заканчивается.

5.      Если nextcall возвращает пустой символ e, то наша задача – перейти в предпоследнюю вершину a^–1 forward-пути, укоротив его на последнюю дугу. Прежде всего проверяем, не является ли вершина a корнем back-дерева. Если да, то алгоритм заканчивает свою работу. При этом, если a=v₀ – начальная вершина графа, то выносится вердикт «совершен гарантированный обход». В противном случае анализируются списки Traversed и Forward для проверки того, является ли пройденный граф графом 2-го рода. Если да, то выносится вердикт «неизвестно, совершен ли обход, но если совершен, то обход гарантированный», в противном случае  – «неизвестно, совершен ли обход, но если совершен, то обход негарантированный». Если же a не является корнем back-дерева, то находим вершину a^–1 (используя двунаправленность списка Forward) и двигаемся с помощью операций call по back-дугам до первой вершины c, лежащей на forward-пути, и далее по forward-дугам до вершины a^–1. Уничтожаем Forward-описание вершины a, удалив его из списка Forward, тем самым, помечая вершину a и укорачивая forward-путь, и заканчиваем шаг. Заметим, что в п.5 мы тоже проходим в графе путь из двух половинок: back- и forward-пути.

Нетрудно видеть, что, если алгоритм не заканчивается в данном шаге, то к концу шага выполнены необходимые условия начала следующего шага.

Обозначив через t_i и call_i, соответственно, число операций и число проходов по дугам (call и nextcall) в пункте i, а через C – некоторую константу, зависящую от программной реализации, имеем: t₁£С, call₁£1, t₂£Сn, call₂=0, t₃£C, call₃=0, t₄£Сn, call₄£n, t₅£Сn, call₅£n. В каждом шаге, кроме последнего, либо 1) выполняются пункты 1,2,3 или 1,2,4 и проходится ровно одна непройденная ранее дуга, либо 2) выполняются пункты 1,5 и помечается ровно одна непомеченная ранее вершина. Очевидно, число шагов вида 1) не превосходит числа дуг k, а число шагов вида 2) – числа вершин n. В результате, через конечное число элементарных операций алгоритм останавливается и общее число операций не превосходит max[ k(t₁+t₂+max(t₃,t₄)), n(t₁+t₅) ] £ k(t₁+t₂+t₄)+n(t₁+t₅) £ k(C+2Cn)+n(C+Cn), то есть, учитывая n £ k–1, равно O(nk), а длина пройденного маршрута не превосходит max[ k(call₁+call₂+max(call₃,call₄)), n(call₁+call₅) ] £ k(call₁+call₂+call₄)+n(call₁+call₅) £ k(1+n)+n(1+n), то есть, учитывая n £ k–1, равно O(nk).

Очевидно также, что алгоритм совершает гарантированный обход любого графа 2-го рода и выносит достоверный вердикт на любом графе. ÿ

4.5. Модификации оптимального алгоритма

Алгоритм A₅ является модификацией алгоритма, предложенного в 1971 г. одним из авторов настоящей статьи [5], для решения более сложной задачи обхода сильно-связных ориентированных графов с помощью робота на графе. Если неизбыточный алгоритм можно рассматривать как ASM на графе, то робот – это конечный автомат на графе. Оценка длины обхода роботом O(nk + n²log₂n). Второе слагаемое возникает из-за того, что алгоритм A₅, используя двунаправленность списка Forward, переходит в предпоследнюю вершину forward-пути (шаг 5) за один проход по циклическому маршруту, а робот вынужден делать много таких проходов. Если не применять специальных оптимизирующих приемов, оценка для робота получится O(nk + n³). Робот в [5] для обхода forward-дерева применяет метод поиска в ширину, что уменьшает оценку до O(nk + n²log₂n). В 1994 г. Y.Afek и E.Gafni в [12] предложили робот, использующий метод поиска в глубину вместе со специальным оптимизирующим приемом, что также дает оценку длины обхода O(nk + n²log₂n). Как мы считаем, сочетание поиска в ширину с этим оптимизирующим приемом должно дать суммарную оценку для робота O(nk + n²log₂log₂n). Для сравнения отметим, что хорошо известный алгоритм Тэрри [10] обхода неориентированных графов тоже является свободным и может быть реализован роботом с длиной обхода 2k и временем работы порядка O(k).

Свободному алгоритму A₅ соответствует неизбыточный алгоритм A₆, проходящий тот же маршрут, но выносящий более точный достоверный вердикт. Более того, его можно оптимизировать так, чтобы после прохода по последней хорде, выходящей из конца forward-пути, возвращаться не в предпоследнюю вершину forward-пути, а в последнюю на forward-пути вершину, из которой выходят еще не пройденные дуги. Алгоритм A₆, соответственно, можно модифицировать для работы с предикатом связующих дуг («минимально избыточный» алгоритм) или с неизбыточным предикатом (неизбыточный алгоритм). Во всех этих модификациях порядок верхней оценки времени работы и длины обхода не меняется. Тем не менее, для некоторых классов графов верхняя оценка минимальной длины обхода может отличаться от O(nk) и на некоторых из них неизбыточный алгоритм работает лучше, чем свободный. Например, для графа на рис.6 свободный алгоритм A₅ имеет оценку W(n²), а неизбыточный алгоритм A₆ – W(n).

Рис.6

Рассматриваемые алгоритмы могут применяться также для покрытия любых достижимых графов с помощью повторных запусков алгоритмов с сохранением информации от предыдущей работы. Иначе говоря, алгоритмы могут работать с графами, для которых определена достоверная операция reset [15], которую они будут использовать только в случае необходимости (в частности, не будут использовать на сильно-связных графах).

Поскольку алгоритм A₅ для каждой дуги, которую он может проходить повторно (дуги back-дерева и forward-пути), хранит в описании начала дуги ссылку на описание ее конца, он может работать на произвольных графах, в процессе своей работы контролируя детерминизм. Для этого после каждой операции call вызывается операция status и возвращенная ею вершина сравнивается с запомненной. При обнаружении недетерминизма алгоритм останавливается с соответствующим вердиктом. Разумеется, если недетерминизм до остановки алгоритма не обнаружен, это не означает, что его нет, просто при данном выполнении нам «повезло».

Еще одной областью применения алгоритма с предикатом (избыточным или неизбыточным) связующих дуг являются многоуровневые графы. Двухуровневый граф можно определить как граф 2-го уровня, в котором вершины являются графами 1-го уровня, причем все эти графы сильно-связны. Более строго, двухуровневый граф можно определить как граф, в котором некоторые дуги промаркированы. Если маркированные дуги удалить, то получится набор изолированных сильно-связных графов – графов 1-го уровня. Если факторизовать двухуровневый граф по отношению взаимной достижимости вершин через немаркированные дуги, то получится сильно-связный граф 2-го уровня.

Если предикат понимать как предикат маркированных дуг, то алгоритм будет обходить двухуровневый граф по уровням: попадая первый раз в некоторый граф 1-го уровня, он сначала полностью его обходит по немаркированным дугам, а потом по маркированной дуге переходит в следующий граф 1-го уровня. При повторном вхождении в граф 1-го уровня, в нем достаточно пройти путь до нужной маркированной дуги, выходящей из графа. Для оценки длины обхода таким алгоритмом можно рассмотреть класс двухуровневых графов, в которых все графы 1-го уровня имеют одинаковое число вершин n₁ и дуг k₁, а граф 2-го уровня имеет n₂ вершин (число графов 1-го уровня) и k₂ дуг. Число вершин и дуг двухуровневого графа n=n₁n₂ и k=k₂+n₂k₁. 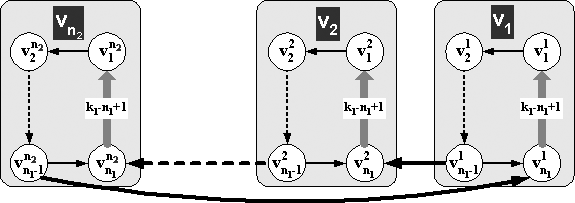Длина обхода равна O(n₂k₂)O(n₁)+n₂O(n₁k₁) = O(n(k₁+k₂)), что при росте k₁ дает предельный выигрыш в n₂ раз. Пример графа приведен на рис.7: графы 1-го уровня (выделены серым фоном) аналогичны графу на рис.2 с начальной вершиной v_n1, граф 2-го уровня аналогичен графу на рис.6, i-ая дуга 2-го уровня ведет из вершины v_n1–1 i-го графа 1-го уровня в начальную вершину v_n1 i+1-го графа 1-го уровня (i меняется по циклу 0..n₂ и показан как верхний индекс вершин).

Рис.7

Пусть две дуги, выходящие из вершин v_n1–1 графов 1-го уровня, упорядочены так, что дуга (vⁱ_n1–1, vⁱ⁺¹_n1) предшествует дуге (vⁱ_n1–1, vⁱ_n1), а дуга (vⁿ²_n1–1, v¹_n1) предшествует дуге (vⁿ²_n1–1, vⁿ²_n1). Тогда алгоритмы A₅ и A₆, «не знающие» о двухуровневой структуре графа, сначала пройдут в графе гамильтонов контур (проходящий через все вершины графа по одному разу), все дуги которого, кроме первой дуги (одной из дуг (v¹_n1, v¹₁)), станут back-дугами. В дальнейшем после прохода по каждой хорде из множества k₁-n₁+1 дуг, обозначенных на рисунке серым цветом, кроме первой и последней в каждом множестве, понадобится пройти весь этот гамильтонов путь. Число таких хорд W(n₂k₁), а длина пути W(n), поэтому длина обхода W(nn₂k₁). В то же время алгоритм, использующий маркировку дуг 2-го уровня, напротив, будет обходить графы 1-го уровня по очереди: сначала обходим i-ый граф, а потом переходим по маркированной дуге в следующий i+1-ый граф. Тем самым, длина обхода будет W(n₂n₁k₁)=W(nk₁), то есть, имеем выигрыш в n₂ раз. Таким образом, если алгоритм «знает» о двухуровневой структуре графа и это «знание» выражено в форме достоверного предиката маркированных дуг, то его обход будет ближе к оптимальному обходу графов такого класса.

p-уровневый граф определяется по индукции как двухуровневый граф, компонентами которого являются p–1-уровневые графы. Алгоритм можно модифицировать для работы с любым наперед заданным числом уровней p.

5.    Тестирование на основе неизбыточных алгоритмов обхода

Предложенные неизбыточные алгоритмы обхода детерминированных ориентированных графов могут служить основой тестирования с открытым состоянием. Дополнительно тест содержит:

Ш        Итератор стимулов (операция next), определяемый предусловием спецификации, которое задает допустимость каждого стимула x в каждом состоянии v автомата: PRE(v,x)=true.

Ш        Медиатор (операции call и status), предназначенный для подачи стимула на тестируемый автомат и получения реакции и постсостояния.

Ш        Оракул, проверяющий правильность перехода и определяемый постусловием спецификации, которое задает допустимость полученных реакции y и постсостояния v` при переходе из пресостояния v по стимулу x: POST(v,x,y,v`)=true.

Мы предполагаем выполненной следующую гипотезу о допустимости для тестирования с открытым состоянием частично определенных автоматов: для каждого состояния, достижимого по модели из начального состояния, все стимулы, допустимые в модели, допустимы и в реализации (обратное не требуется).

Тестирование со скрытым состоянием – гораздо более сложная задача. Прежде всего, возникает проблема допустимости стимулов для частично определенных автоматов. Если мы не знаем, в каком состоянии находится тестируемый автомат, то мы не знаем, какие стимулы в нем допустимы, а какие нет. Если не делать никаких допущений о реализации, то мы можем подавать только такие стимулы, которые допустимы во всех состояниях. Это одна из причин, по которой часто рассматриваются только полностью определенные автоматы [15].

Спецификация автомата, вообще говоря, может определять несколько спецификационных переходов из данного пресостояния по данному стимулу с получением одной и той же реакции; такие переходы различаются только своим постсостоянием. Иными словами, уравнение постусловия POST(v,x,y,v`)=true может иметь более одного решения относительно постсостояния v`. Если для любых возможных v,x,y таких решений не более одного, то будем говорить, что спецификация и описываемый ею модельный автомат слабо-детерминированы. В [21] это называется наблюдаемым недетерминизмом.

Следует отметить, что слабый детерминизм не уменьшает описательную мощность спецификаций с точностью до эквивалентности специфицируемых автоматов. Дело в том, что классу эквивалентных конечных автоматов соответствует регулярное множество последовательностей в алфавите стимулов и реакций (в декартовом произведении их алфавитов), которое, по известной теореме о регулярных множествах [2,4,11], может быть порождено детерминированным конечным графом. Детерминизм здесь понимается как отсутствие двух одинаково раскрашенных (стимулом и реакцией) дуг, выходящих из одной вершины, что эквивалентно слабому детерминизму в нашем определении. Другое дело, что спецификации без ограничения слабо-детерминированности часто писать проще, а определение эквивалентных слабо-детерминированных спецификаций может быть трудным делом.

Для тестирования со скрытым состоянием частично определенных автоматов со слабо-детерминированной спецификацией, примем следующую гипотезу о допустимости: для данных пресостояния, допустимого в нем стимула и реакции любой стимул, допустимый в постсостоянии спецификационного перехода, допустим и в постсостоянии реализационного перехода. Если через x(v) обозначить множество стимулов, допустимых в состоянии v, то наша гипотеза означает вложенность x(v`)Íx(v<sub>R</sub>), где v<sub>R</sub> – постсостояние реализационного перехода (v,x,y,v<sub>R</sub>), а v` – решение уравнения постусловия POST(v,x,y,v`)=true. Если уравнение не имеет решений, то это означает неправильность реакции y, и на этом тестирование прекращается.

Гипотеза о допустимости, кажущаяся на первый взгляд немотивированной, на практике оказывается вполне естественной. Она означает, что допустимость стимулов в каждый момент времени однозначно определяется историей (последовательностью подаваемых стимулов и получаемых реакций), что вполне естественно при работе пользователя с программной системой, моделируемой автоматом. Естественно, предполагается, что ошибки, возможные в реализации, могут быть обнаружены (по получаемым реакциям) до того, как они приведут к нарушению «гипотезы о допустимости».

Предположим, что мы можем определить правильность реакции и для правильной реакции вычислить постсостояние. Например, постусловие имеет вид “ReactionChecking(v,x,y) & v`=Poststate(v,x,y)”, где ReactionChecking – предикат, определяющий правильность реакции, а Poststate – эксплицитная функция, вычисляющая постсостояние для правильной реакции. Тогда тестирование можно вести следующим образом.

Будем считать, что начальное состояние v₀ известно. Подав на него стимул x₀ и получив реакцию y₀, мы проверяем правильность реакции и, если она правильная, вычисляем постсостояние v₁. Тогда, согласно «гипотезе о допустимости», реализация находится в постсостоянии, в котором допустимы все стимулы, допустимые в v₁. Исходя из этого, на следующем шаге выбираем стимул, допустимый в v₁, и так далее. В процессе такого тестирования будем строить гипотетический граф и маршрут в нем, проводя дуги, соответствующие гипотетическим переходам автомата. Если какая-то реакция отвергается, то тест фиксирует ошибку, и тестирование заканчивается.

Важно подчеркнуть следующее: если реализационный автомат детерминирован, то построенный гипотетический граф также детерминирован. Отчасти это дает возможность контролировать допущение о детерминизме реализационного графа. Более важно то, что если пройденный маршрут является обходом построенного графа, то мы можем считать построенный граф графом состояний эксплицированного подавтомата M(R) модельного автомата M. Реализационный автомат R (в котором не учитываются «лишние» стимулы, допустимые в реализации, но недопустимые в спецификации) удовлетворяет спецификации тогда и только тогда, когда он эквивалентен подавтомату M(R). После этого можно проверять эту эквивалентность, используя обычные методы тестирования соответствия с помощью проверяющих последовательностей, рассматривая граф M(R) в качестве модельного графа.

Таким образом, мы видим, что неизбыточные алгоритмы обхода могут использоваться в качестве базовых в первой фазе тестирования со скрытым состоянием, которую можно назвать фазой эксплицирования модели. Условием являются детерминизм реализации, слабый детерминизм спецификации и возможность определения правильности реакции и вычисления постсостояния для правильной реакции, а также «гипотеза о допустимости». Вторая фаза тестирования – это обычное тестирование соответствия автоматов с использованием эксплицированного графа в качестве модели.

Недетерминированной (в частности, слабо-детерминированной) спецификации, конечно, может соответствовать недетерминированная реализация. Часто при тестировании прибегают к факторизации спецификации, вводя эквивалентность переходов [29,22]. Ближайшей целью такой факторизации является  уменьшение требуемого числа тестовых воздействий как следствие уменьшения числа состояний и переходов в факторизованном модельном автомате. При таком тестировании требуется проверять только фактор-переходы, для чего может быть выбран любой переход из соответствующего класса эквивалентности. Понятно, что если заданную эквивалентность «раздробить», то тестирование по фактор-модели с более «дробной» эквивалентностью даст не худшее тестовое покрытие. Существуют методы такого дальнейшего «дробления» заданной эквивалентности, которые в некоторых случаях приводят к детерминированности фактор-модели, оставляя ее все еще достаточно «малой» по сравнению с исходной нефакторизованной моделью [24]. Таким образом, наши неизбыточные алгоритмы обхода детерминированных графов могут применяться также при факторизованном тестировании недетерминированных реализаций.

6.    Заключение

Предложенные в настоящей статье неизбыточные алгоритмы обхода графов и тестирование на их основе были разработаны и апробированы, начиная с 1995 г., группой RedVerst [1] в ходе выполнения нескольких масштабных проектов по тестированию разнообразного программного обеспечения [29,22], которое велось на основе функциональных спецификаций, полученных на стадии проектирования или реинжениринга.

Как правило, при тестировании критичным является не столько сложность по времени и памяти алгоритма обхода, сколько число тестовых воздействий, то есть, длина обхода. Свободный алгоритм A₅ (и его неизбыточная версия A₆) обеспечивают лишь минимальный порядок nk длины обхода в наихудшем случае. В то же время на многих графах с минимальной длиной обхода по порядку меньшей nk, они могут строить обход столь же длинный, как и в наихудшем случае. Исследование неизбыточных алгоритмов, стремящихся совершить обход минимальной длины, в последнее время активно развивается (см. например, [25]).

В следующей статье мы рассмотрим алгоритмы обходы недетерминированных графов, которые могут использоваться как основа тестирования недетерминированных автоматов. Там также будут рассмотрены два случая: 1) тестирование с открытым состоянием и 2) первая фаза (эксплицирование модельного автомата) тестирования со скрытым состоянием при условии слабой детерминированности спецификации.

Литература

1.                    http://www.ispras.ru/~RedVerst/

2.                    Рабин М., Скотт Д., Конечные автоматы и проблемы их разрешения. Кибернетический сборник, ИЛ, вып. 4 (1962), 58-91.

3.                    M.O. Rabin, Maze Threading Automata. An unpublished lecture presented at MIT and UC Berkeley, 1967.

4.                    Сеймур Гинзбург. Математическая теория контекстно-свободных языков. М., «МИР», 1970, 71-78.

5.                    И.Б.Бурдонов, Изучение поведения автоматов на графах. Дипломная работа, МГУ им. М.В.Ломоносова, механико-математический факультет, 1971 г.

6.                    J. Edmonds, E. L. Johnson. Matching, Euler Tours and the Chinese Postman, Mathematical Programming, 5:88124, 1973.

7.                    J. K. Lenstra, A. H. G. Rinnooy Kan. On General Routing Problems. Networks 6:273280, 1976.

8.                    M. Blum and W.J. Sakoda, On the Capability of Finite Automata in 2 and 3 Dimensional Space. In Proceeding of the Eighteenth Annual Symposium on Foundations of Computer Science, 1977. pp. 147-161.

9.                    S. Even, Graph Algorithms, Computer Science press, 1979.

10.                О.Оре. Теория графов. Пер. с англ., 2-е изд., М., «Наука», 1980

11.                Д.В.Варсанофьев, А.Г.Дымченко. Основы компиляции. 1991. http://www.codenet.ru/progr/compil/cmp/intro.php

12.                Y. Afek and E. Gafni, Distributed Algorithms for Unidirectional Networks, SIAM J. Comput., Vol. 23, No. 6, 1994, pp. 1152-1178.

13.                G. von Bochmann, A. Petrenko. Protocol Testing: Review of Methods and Relevance for Software Testing. Proceeding of ISSTA 1994, pp. 109-124.

14.                A. Petrenko, N. Yevtushenko, R. Dssouli. Grey-Box FSM-based Testing Strategies. Department Publication 911, University de Montreal, 1994, 22 p.

15.                D. Lee and M. Yannakakis. Principles and methods of testing finite state machines - a survey. Proceedings of the IEEE, vol. 84, 8:1090-1123, Berlin, IEEE Computer Society Press, Aug. 1996.

16.                A. Petrenko, N. Yevtushenko, G. von Bochmann. Testing deterministic implementations from nondeterministic FSM specifications. Selected proceedings of the IFIP TC6 9-th international workshop on Testing of communicating systems, September 1996.

17.                D. Hoffman, P.Strooper. ClassBench: a Framework for Automated Class Testing. Software Maintenance: Practice and Experience, Vol. 27, No. 5, May 1997, pp. 573-579.

18.                S. Even, A. Litman and P. Winkler, Computing with Snakes in Directed Networks of Automata. J. of Algorithms, Vol. 24, 1997, pp. 158-170.

19.                L. Murray, D. Carrington. I. MacColl, J. McDonald, P. Strooper. Formal Derivation of Finite State Machines for Class Testing. In J.P. Bowen, A.Fett, M.G.Hinchey, editors, ZUM'98: The Z Formal Specification Notation., 11-th Int. Conf. of Z Users, Vol. 1493 of Lecture Notes in Computer Science. Springer-Verlag, 1998, pp. 42-59.

20.                X. Deng and C.H. Papadimitriou, Exploring an Unknown Graph, J.of Graph Th., Vol. 32, No. 3, 1999, pp. 265-297.

21.                Marine Tabourier, Ana Cavalli and Melania Ionescu , A GSM-MAP Protocol Experiment Using Passive Testing, Proceeding of FM'99 (World Congress on Formal methods in development of Computing Systems), Toulouse (France), 20-24 September 1999.

22.                I. Bourdonov, A. Kossatchev, A. Petrenko, and D. Galter. KVEST: Automated Generation of Test Suites from Formal Specifications. FM’99: Formal Methods. LNCS, vol. 1708, pp. 608621, Springer-Verlag, 1999.

23.                M. A. Fecko, M. U. Uyar, A. S. Sethi, and P. D. Amer. Conformance testing in systems with semicontrollable interfaces. Annals of Telecommunications, 55(1):7083, Jan. 2000.

24.                И.Б.Бурдонов, А.С.Косачев, В.В.Кулямин. Использование конечных автоматов для тестирования программ. "Программирование", 2000, №2.

25.                S. Albers and M.R. Henzinger, Exploring Unknown Environments, SIAM J. Comput., Vol. 29, No. 4, 2000, pp. 1164-1188.

26.                Yuri Gurevich, "Sequential Abstract State Machines Capture Sequential Algorithms", ACM Transactions on Computational Logic, vol. 1, no. 1, July 2000, 77-111.

27.                H. Thimbleby. The directed Chinese Postman Problem. Technical Report, School of Computing Science, Middlesex University, Bounds Green Road, LONDON, 2000.

28.                BHATT, S., EVEN S., GREENBERG, D., and TAYAR, R., "Traversing directed eulerian mazes'', Graph Theoretic Concepts in Computer Science, Proceedings of WG'2000, U. Brandes and D. Wagner (eds), Lecture Notes in Computer Science No. 1928, pp. 35-46, Springer, 2000.

29.                I. Bourdonov, A. Kossatchev, V. Kuliamin, and A. Petrenko. UniTesK Test Suite Architecture. Proceedings of FME 2002. LNCS 2391, pp. 77-88, Springer-Verlag, 2002.