Как правило под "числом" мы будем иметь в виду неотрицательное целое число.
Обозначение 4.1:1: Для n>0 через I(n) обозначим множество целых чисел от 0 до n-1.
Мы будем рассматривать также двоичное представление числа. Если x![]() I(2m),
то x имеет m двоичных разрядов 0,1,...,m-1.
I(2m),
то x имеет m двоичных разрядов 0,1,...,m-1.
Обозначение 4.1:2: Для x![]() I(2m)
и r
I(2m)
и r![]() I(m) через
x|r обозначим значение r-го двоичного разряда числа x.
I(m) через
x|r обозначим значение r-го двоичного разряда числа x.
m-1 x
I(2m) однозначно раскладывается x =
2r*(x|r) r=0
Определение 4.1:1: Для x![]() I(2),
то есть x=0,1, его отрицанием называется число
I(2),
то есть x=0,1, его отрицанием называется число ![]() x,
определяемое следующим образом:
x,
определяемое следующим образом:
x =
0, если x=1 1, если x=0
Определение 4.1:2: Для x![]() I(2m)
его отрицанием называется число
I(2m)
его отрицанием называется число ![]() x,
которое есть поразрядное отрицание x, то есть число, в котором значение
каждого двоичного разряда есть отрицание значения соответствующего разряда числа
x:
x,
которое есть поразрядное отрицание x, то есть число, в котором значение
каждого двоичного разряда есть отрицание значения соответствующего разряда числа
x: ![]() r
r![]() I(m)
(
I(m)
(![]() x)|r =
x)|r = ![]() (x|r).
Числа x и
(x|r).
Числа x и ![]() x будем
называть взаимно-инвертированными.
x будем
называть взаимно-инвертированными.
Определение 4.1:3: Для x,y![]() I(2),
то есть x,y=0,1, исключающей дизъюнкцией чисел x и y называется число x
I(2),
то есть x,y=0,1, исключающей дизъюнкцией чисел x и y называется число x![]() y,
определяемое следующим образом:
y,
определяемое следующим образом:
x y =
0, если x=y 1, если x y0
Определение 4.1:4: Для x,y![]() I(2m)
исключающей дизъюнкцией чисел x и y называется число x
I(2m)
исключающей дизъюнкцией чисел x и y называется число x![]() y,
которое есть поразрядная исключающая дизъюнкция x и y, то есть число,
в котором значение каждого двоичного разряда есть исключающая дизъюнкция значений
соответствующих разрядов чисел x и y:
y,
которое есть поразрядная исключающая дизъюнкция x и y, то есть число,
в котором значение каждого двоичного разряда есть исключающая дизъюнкция значений
соответствующих разрядов чисел x и y: ![]() r
r![]() I(m)
(x
I(m)
(x![]() y)|r = (x|r)
y)|r = (x|r)![]() (y|r).
Число y, фактически, задаёт те двоичные разряды числа x, которые инвертируются
при переходе к x
(y|r).
Число y, фактически, задаёт те двоичные разряды числа x, которые инвертируются
при переходе к x![]() y.
y.
Теорема 4.1:1: ![]() x,y
x,y![]() I(2m)
(
I(2m)
(![]() x)
x)![]() y
=
y
= ![]() (x
(x![]() y).
y).
Доказательство:
Это утверждение легко проверяются для m=1 (Определения 1,3) и очевидным образом распространяется для поразрядных операций (Определения 2,4).
Обозначение 4.2:1: Группу всех взаимно-однозначных
преобразований (подстановок) множества I(n) по операции умножения преобразований,
определяемой как их последовательное выполнение, иначе называемую группой подстановок,
или симметрической группой, степени n, обозначим через ![]() (n).
Тождественное преобразование (единица группы) будем обозначать
(n).
Тождественное преобразование (единица группы) будем обозначать ![]() .
.
Обозначение 4.2:2: Подстановку ![]()
![]()
![]() (n)
множества I(n) можно записать в виде:
(n)
множества I(n) можно записать в виде:
n-1, n-2, ...,1, 0 или, считая верхний ряд фиксированным: (n-1) ,(n-2)
,...,1
,0
( (n-1) ,(n-2)
,...,1
,0
)
Теорема 4.2.1:1: Множество I(2m)
по операции ![]() является
коммутативной группой со следующими свойствами:
является
коммутативной группой со следующими свойствами:
Доказательство:
Все эти свойства легко проверяются для m=1 (Определения 4.1:1,3) и очевидным образом распространяется для поразрядных операций (Определения 4.1:2,4).
Обозначение 4.2.1:1: Для t![]() I(2m)
отображение
I(2m)
отображение ![]() :I(2m)
:I(2m)![]() I(2m),
определяемое
I(2m),
определяемое ![]() x
x![]() I(2m)
x
I(2m)
x![]() =x
=x![]() t,
будем обозначать
t,
будем обозначать ![]() (t).
(t).
Теорема 4.2.1:2: Если t![]() I(2m),
то отображение
I(2m),
то отображение ![]() (t)
является подстановкой множества I(2m), то есть
(t)
является подстановкой множества I(2m), то есть ![]() (t)
(t)![]()
![]() (2m).
(2m).
Доказательство:
Нужно доказать, что отображение ![]() (t)
является биекцией (взаимно-однозначным отображением) I(2m)
на I(2m), то есть оно a) инъективно и b) сюръективно.
(t)
является биекцией (взаимно-однозначным отображением) I(2m)
на I(2m), то есть оно a) инъективно и b) сюръективно.
a) Отображение ![]() (t)
инъективно, то есть разным x соответствуют разные x
(t)
инъективно, то есть разным x соответствуют разные x![]() (t):
(t):
![]() x1,x2
x1,x2![]() I(2m)
x1
I(2m)
x1![]() x2
x2
![]() x1
x1![]() (t)
(t)![]() x2
x2![]() (t).
(t).
Действительно, если x1
x2, то
r
I(m) x1|r
x2|r, поэтому, как непосредственно следует из определения операции
, (x1|r)
(t|r)
(x2|r)
(t|r)
x1
t
x2
t, то есть x1
(t)
x2
(t).
b) Отображение ![]() (t)
сюръективно, то есть это отображение I(2m) на I(2m),
то есть
(t)
сюръективно, то есть это отображение I(2m) на I(2m),
то есть ![]() x
x![]() I(2m)
I(2m)
![]() y
y![]() I(2m)
такое, что yt(
I(2m)
такое, что yt(![]() )=x.
)=x.
Действительно, если y=x
t, то yt(
)=y
t=(x
t)
t=x
(t
t)=x
0=x.
Определение 4.2.1:1: Для t![]() I(2m)
преобразование
I(2m)
преобразование ![]() =
=![]() (t),
определяемое
(t),
определяемое ![]() x
x![]() I(2m)
x
I(2m)
x![]() (t)=x
(t)=x![]() t,
назовём инвертирующим порядка 2m, поскольку
t,
назовём инвертирующим порядка 2m, поскольку ![]() определяется инвертированием некоторых двоичных разрядов чисел из I(2m).
определяется инвертированием некоторых двоичных разрядов чисел из I(2m).
Теорема 4.2.1:3: Число инвертирующих преобразований порядка 2m равно 2m.
Доказательство очевидно.
Обозначение 4.2.1:2: Множество инвертирующих
преобразований обозначим T(2m) и для
![]()
![]() T(2m)
соответствующее число t
T(2m)
соответствующее число t![]() I(2m)
будем обозначать t=t(
I(2m)
будем обозначать t=t(![]() ).
).
Теорема 4.2.1:4: Множество T(2m)
есть подгруппа группы T(2m) изоморфная
группе I(2m) по операции![]() .
.
Доказательство:
Соответствие ![]() =
=![]() (t)
можно рассматривать как соответствие I(2m) и T(2m).
Оно, очевидно:
(t)
можно рассматривать как соответствие I(2m) и T(2m).
Оно, очевидно:
a) является отображением, то есть каждому t![]() I(2m)
ставит в соответствие только одно
I(2m)
ставит в соответствие только одно ![]() (t)
в силу определения
(t)
в силу определения ![]() (t);
(t);
b) сюръективно, то есть это отображение I(2m) на T(2m) в силу определения T(2m);
c) инъективно, то есть ![]() t1,t2
t1,t2![]() I(2m)
t1
I(2m)
t1![]() t2
t2
![]()
![]() (t1)
(t1)![]() (t2);
(t2);
действительно, t1 ![]() t2
t2
![]() 0
0![]() t1
t1
![]() 0
0![]() t2,
то есть 0
t2,
то есть 0![]() (t1)
(t1)
![]() 0
0![]() (t2).
(t2).
Для доказательства изоморфизма нужно показать, что ![]() (t1
(t1![]() t2)
=
t2)
= ![]() (t1)
(t1)![]() (t2).
Действительно,
(t2).
Действительно, ![]() x
x![]() I(2m)
x
I(2m)
x![]() (t1
(t1![]() t2)
= x
t2)
= x![]() (t1
(t1![]() t2)
= (x
t2)
= (x![]() t1)
t1)![]() t2
= (x
t2
= (x![]() (t1))
(t1))![]() t2)
= (x
t2)
= (x![]() (t1))
(t1))![]() (t2)
= x(
(t2)
= x(![]() (t1)
(t1)![]() (t2)).
(t2)).
Теорема 4.2.1:5: Инвертирующее преобразование,
обратное данному инвертирующему преобразованию, совпадает с ним самим: ![]()
![]()
![]() T(2m)
T(2m)
![]() -1=
-1=![]() .
.
Доказательство:
![]() x
x![]() I(2m)
x(
I(2m)
x(![]()
![]() )
= (x
)
= (x![]() )
)![]() = (x
= (x![]() t(
t(![]() ))
))![]() = (x
= (x![]() t(
t(![]() ))
))![]() t(
t(![]() )
= x
)
= x![]() (t(
(t(![]() )
)![]() t(
t(![]() ))
= x
))
= x![]() 0 = x.
Поэтому
0 = x.
Поэтому ![]() -1=
-1=![]() .
.
Теорема 4.2.1:6: Подгруппа T(2m)имеет
систему образующих из m преобразований ![]() r
=
r
= ![]() (2r),
где r
(2r),
где r![]() I(m).
I(m).
Доказательство:
| m-1 | ||
| Поскольку |
2r*(x|r) | |
| r=0 |
и поскольку операция ![]() определена поразрядно, доказательство теоремы очевидно.
определена поразрядно, доказательство теоремы очевидно.
Теорема 4.2.2:1: Если {M,![]() }
- группа на множестве M с операцией
}
- группа на множестве M с операцией ![]() ,
и на том же множестве M определена операция
,
и на том же множестве M определена операция ![]() :
:
![]() x,y
x,y![]() M
x
M
x![]() y=y
y=y![]() x,
то {M,
x,
то {M,![]() }
будет группой, изоморфной группе {M,
}
будет группой, изоморфной группе {M,![]() }.
}.
Доказательство:
Рассмотрим отображение ![]() :M
:M![]() M,
ставящее в соответствие каждому элементу его обратный элемент в группе {M,
M,
ставящее в соответствие каждому элементу его обратный элемент в группе {M,![]() }:
}:
![]() x
x![]() M
x
M
x![]() =x-1.
Очевидно, что
=x-1.
Очевидно, что ![]() есть взаимно-однозначное отображение M на M. Для доказательства изоморфизма
осталось показать, что (x
есть взаимно-однозначное отображение M на M. Для доказательства изоморфизма
осталось показать, что (x![]() y)
y)![]() =x
=x![]()
![]() y
y![]() .
Действительно: (x
.
Действительно: (x![]() y)
y)![]() =(y
=(y![]() x)
x)![]() =(y
=(y![]() x)-1=x-1
x)-1=x-1![]() y-1=x
y-1=x![]()
![]() y
y![]() .
.
Обозначение 4.2.2:1: Для ![]()
![]()
![]() (m)
отображение
(m)
отображение ![]() :I(2m)
:I(2m)![]() I(2m),
определяемое
I(2m),
определяемое ![]() x
x![]() I(2m)
I(2m)
![]() r
r![]() I(m)
(x
I(m)
(x![]() )|r=x|(r
)|r=x|(r![]() )
будем обозначать
)
будем обозначать ![]() (
(![]() ).
).
Теорема 4.2.2:2: Если ![]()
![]()
![]() (m),
то отображение
(m),
то отображение ![]() (
(![]() )
является подстановкой множества I(2m), то есть
)
является подстановкой множества I(2m), то есть ![]() (
(![]() )
)![]()
![]() (2m).
(2m).
Доказательство:
Нужно доказать, что отображение ![]() (
(![]() )
является биекцией (взаимно-однозначным отображением) I(2m)
на I(2m), то есть оно a) инъективно и b) сюръективно.
)
является биекцией (взаимно-однозначным отображением) I(2m)
на I(2m), то есть оно a) инъективно и b) сюръективно.
a) Отображение ![]() (
(![]() )
инъективно, то есть разным x соответствуют разные x
)
инъективно, то есть разным x соответствуют разные x![]() (
(![]() ):
):
![]() x1,x2
x1,x2![]() I(2m)
x1
I(2m)
x1![]() x2
x2
![]() x1
x1![]() (
(![]() )
)![]() x2
x2![]() (
(![]() ).
).
Действительно, если x1![]() x2,
то
x2,
то ![]() r
r![]() I(m)
x1|r
I(m)
x1|r![]() x2|r.
В силу того, что
x2|r.
В силу того, что ![]() - подстановка множества I(m),
- подстановка множества I(m), ![]() r1
r1![]() I(m)
r=r1
I(m)
r=r1![]() и значит x1|(r1
и значит x1|(r1![]() )
)![]() x2|(r1
x2|(r1![]() ),
то есть x1
),
то есть x1![]() (
(![]() )
)![]() x2
x2![]() (
(![]() ).
).
b) Отображение ![]() (
(![]() )
сюръективно, то есть это отображение I(2m) на I(2m),
то есть
)
сюръективно, то есть это отображение I(2m) на I(2m),
то есть ![]() x
x![]() I(2m)
I(2m)
![]() y
y![]() I(2m)
такое, что y
I(2m)
такое, что y![]() (
(![]() )=x.
)=x.
Действительно, если y=x![]() (
(![]() -1),
то
-1),
то ![]() r
r![]() I(2m)
(y
I(2m)
(y![]() (
(![]() ))|r=y|(r
))|r=y|(r![]() )=(x
)=(x![]() (
(![]() -1))|(r
-1))|(r![]() )=x|((r
)=x|((r![]() )
)![]() -1)=x|(r(
-1)=x|(r(![]()
![]() -1))=x|r,
то есть y
-1))=x|r,
то есть y![]() (
(![]() )
и x совпадают по всем двоичным разрядам и значит x=y
)
и x совпадают по всем двоичным разрядам и значит x=y![]() (
(![]() ).
).
Определение 4.2.2:1: Для ![]()
![]()
![]() (m)
преобразование
(m)
преобразование ![]() =
=![]() (
(![]() ),
определяемое
),
определяемое ![]() x
x![]() I(2m)
I(2m)
![]() r
r![]() I(m)
(x
I(m)
(x![]() )|r=x|(r
)|r=x|(r![]() ),
назовём перестановочным порядка 2m, поскольку
),
назовём перестановочным порядка 2m, поскольку ![]() определяется некоторой перестановкой двоичных разрядов чисел из I(2m).
определяется некоторой перестановкой двоичных разрядов чисел из I(2m).
Теорема 4.2.2:3: Число перестановочных преобразований порядка 2m равно m!.
Доказательство очевидно.
Обозначение 4.2.2:2: Множество перестановочных
преобразований обозначим P(2m)
и для ![]()
![]() P(2m)
соответствующую подстановку
P(2m)
соответствующую подстановку ![]()
![]()
![]() (m)
будем обозначать
(m)
будем обозначать ![]() =
=![]() (
(![]() ).
).
Теорема 4.2.2:4: Множество P(2m)
есть подгруппа группы ![]() (2m)
изоморфная группе
(2m)
изоморфная группе ![]() (m).
(m).
Доказательство:
Соответствие ![]() =
=![]() (
(![]() )
можно рассматривать как соответствие
)
можно рассматривать как соответствие ![]() (m)
и P(2m). Оно, очевидно:
(m)
и P(2m). Оно, очевидно:
a) является отображением, то есть каждому ![]()
![]()
![]() (m)
ставит в соответствие только одно
(m)
ставит в соответствие только одно ![]() (
(![]() )
в силу определения
)
в силу определения ![]() (
(![]() );
);
b) сюръективно, то есть это отображение ![]() (m)
на
(m)
на ![]() (2m)
в силу определения P(2m);
(2m)
в силу определения P(2m);
c) инъективно, то есть ![]()
![]() 1,
1,![]() 2
2![]()
![]() (m)
(m)
![]() 1
1![]()
![]() 2
2
![]()
![]() (
(![]() 1)
1)![]() (
(![]() 2);
действительно,
2);
действительно, ![]() 1
1![]()
![]() 2
2
![]()
![]() r
r![]() I(m)
r
I(m)
r![]() 1
1![]() r
r![]() 2,
и значит для x, имеющего "1" в разряде r
2,
и значит для x, имеющего "1" в разряде r![]() 1
и "0" в разряде r
1
и "0" в разряде r![]() 2,
x|(r
2,
x|(r![]() 1)
1)
![]() x|(r
x|(r![]() 2),
то есть (x
2),
то есть (x![]() (
(![]() 1))|r
1))|r
![]() (x
(x![]() (
(![]() 2))|r.
2))|r.
Теперь покажем, что ![]() (
(![]() 1
1![]() 2)=
2)=
![]() (
(![]() 2)
2)
![]() (
(![]() 1).
Действительно,
1).
Действительно, ![]() x
x![]() I(2m)
I(2m)
![]() r
r![]() I(m)
(x
I(m)
(x ![]() (
(![]() 1
1![]() 2))|r=x|(r(
2))|r=x|(r(![]() 1
1![]() 2))=x|((r
2))=x|((r![]() 1)
1)![]() 2)=(x
2)=(x
![]() (
(![]() 2))|(r
2))|(r![]() 1)=((x
1)=((x
![]() (
(![]() 2))
2))
![]() (
(![]() 1))|r=(x(
1))|r=(x(
![]() (
(![]() 2)
2)
![]() (
(![]() 1)))|r.
1)))|r.
Таким образом, ![]() (m)
изоморфно P(2m) с операцией "обратного
последовательного выполнения преобразований". В силу теоремы
1
(m)
изоморфно P(2m) с операцией "обратного
последовательного выполнения преобразований". В силу теоремы
1 ![]() (m)
изоморфно также P(2m) с нормальной операцией
"прямого последовательного выполнения преобразований".
(m)
изоморфно также P(2m) с нормальной операцией
"прямого последовательного выполнения преобразований".
Теорема 4.2.2:5: Перестановочное преобразование,
обратное данному перестановочному преобразованию, определяется перестановкой
двоичных разрядов чисел, обратной перестановке, определяющей данное перестановочное
преобразование: ![]()
![]()
![]() P(2m)
P(2m)
![]() (
(![]() -1)=(
-1)=(![]() (
(
![]() ))-1.
))-1.
Доказательство:
![]() x
x![]() I(2m)
2
I(2m)
2 ![]() r
r![]() I(m)
x(
I(m)
x(![]() (
(![]() )
)![]() (
(![]() -1))|r
= ((x
-1))|r
= ((x![]() (
(![]() ))
))![]() (
(![]() -1)|r
= (x
-1)|r
= (x![]() (
(![]() ))|(r
))|(r![]() -1)
= x|((r
-1)
= x|((r![]() -1)
-1)![]() )
= x|(r(
)
= x|(r(![]() -1
-1![]() ))
= x|(r
))
= x|(r![]() )
= x|r.
)
= x|r.
Поэтому ![]() (
(![]() )
)![]() (
(![]() -1)=
-1)=![]() ,
то есть
,
то есть ![]() (
(![]() )-1
=
)-1
= ![]() (
(![]() -1),
то есть
-1),
то есть ![]() (
(![]() -1)=(
-1)=(![]() (
(
![]() ))-1.
))-1.
Теорема 4.2.2:6: Подгруппа P(2m)
имеет систему образующих из двух элементов: ![]() 0
=
0
= ![]() (
(![]() 0)
и
0)
и ![]() 1
=
1
= ![]() (
(![]() 1),
где
1),
где
0 = (m-2,m-1,...,3,2,0,1) - транспозиция чисел 0 и 1
1 = (m-2,m-3,...,1,0,m-1) - циклический сдвиг всех элементов
Доказательство: Согласно известной теореме теории групп, ![]() (m)
имеет систему образующих {
(m)
имеет систему образующих { ![]() 0,
0,![]() 1}.
Поскольку
1}.
Поскольку ![]() (m)
изоморфно
(m)
изоморфно ![]() (2m),
теорема доказана.
(2m),
теорема доказана.
Определение 4.2.3:1: Логическим преобразованием порядка 2m назовём преобразование, которое является преобразованием или произведением нескольких преобразований, каждое из которых - это инвертирующее или перестановочное преобразование порядка 2m.
Обозначение 4.2.3:1: Множество логических преобразований
обозначим ![]() (2m).
(2m).
Теорема 4.2.3:1: Множество логических преобразований
![]() (2m)
является подгруппой группы
(2m)
является подгруппой группы ![]() (2m).
(2m).
Доказательство очевидно.
Теорема 4.2.3:2: Группы T(2m)
и P(2m) имеют единственный общий элемент
- тождественное преобразование: T(2m)![]() P(2m)=
P(2m)=![]() .
.
Доказательство:
Пусть ![]()
![]() T(2m)
T(2m)
![]()
![]()
![]()
![]()
![]() P(2m);
t=t(
P(2m);
t=t(![]() )
) ![]() =
=![]() (
(![]() ).
Поскольку
).
Поскольку ![]()
![]()
![]() , t
, t ![]() 0 и
поэтому t
0 и
поэтому t![]()
![]() 0
(
0
(![]() не изменяет
количество "1" в двоичном представлении числа), но t
не изменяет
количество "1" в двоичном представлении числа), но t![]() =t
=t![]() t=0.
Следовательно, t
t=0.
Следовательно, t![]()
![]() t
t![]() и, значит,
и, значит, ![]()
![]()
![]() .
.
Лемма 4.2.3:1: ![]() x,y
x,y![]() I(2m)
I(2m)
![]()
![]()
![]() P(2m)
(x
P(2m)
(x![]() y)
y)![]() =(x
=(x![]() )
)![]() (y
(y![]() ).
).
Доказательство:
Пусть ![]() =
=![]() (
(![]() ).
).
r
I(m)
((x y)
)|r
= (по определению )
= (x y)|(r
)
= (по определению )
= (x|(r ))
(y|(r
))
= (по определению )
= ((x )|r)
((y
)|r)
= (по определению )
= ((x )
(y
))|r.
Следовательно, (x![]() y)
y)![]() =(x
=(x![]() )
)![]() (y
(y![]() ),
что и требовалось доказать.
),
что и требовалось доказать.
Теорема 4.2.3:3: Группа T(2m)
перестановочна с любым преобразованием из P(2m):
![]()
![]()
![]() P(2m)
P(2m)
![]() T(2m)=
T(2m)
T(2m)=
T(2m)![]() .
Как следствие подгруппы T(2m) и P(2m)
перестановочны: T(2m)P(2m)
= P(2m)T(2m).
.
Как следствие подгруппы T(2m) и P(2m)
перестановочны: T(2m)P(2m)
= P(2m)T(2m).
Доказательство:
Нужно доказать, что ![]()
![]()
![]() P(2m)
P(2m)
![]()
![]()
![]() T(2m)
T(2m)
![]()
![]() 1,
1,![]() 2
2![]() T(2m)
такие, что
T(2m)
такие, что ![]()
![]() =
=![]() и
и ![]()
![]() =
= ![]()
![]() 2.
2.
Обозначая t=t(![]() ),
возьмём t1=t
),
возьмём t1=t![]() -1
и, соответственно,
-1
и, соответственно, ![]() 1=
1=![]() (t1).
Тогда t=t1
(t1).
Тогда t=t1![]() и
и ![]() x
x![]() I(2m)
x(
I(2m)
x(![]()
![]() )
= (x
)
= (x![]() )
)![]() = (x
= (x![]() )
)![]() t
= (x
t
= (x![]() )
)![]() (t1
(t1![]() )
= (по Лемме 1) = (x
)
= (по Лемме 1) = (x![]() t1)
t1)
![]() = (x
= (x![]() 1)
1)![]() = x(
= x(![]() 1
1![]() ).
Итак:
).
Итак: ![]() x
x![]() I(2m)
x(
I(2m)
x(![]()
![]() )
= x(
)
= x(![]() 1
1![]() ),
то есть
),
то есть ![]()
![]() =
= ![]() 1
1![]() .
Если теперь t2 =t
.
Если теперь t2 =t![]() ,
то t=t2
,
то t=t2![]() -1
и для
-1
и для ![]() 2
=
2
= ![]() (t2),
как только что доказано,
(t2),
как только что доказано, ![]()
![]() 2
=
2
= ![]()
![]() .
.
Теорема 4.2.3:4: Подгруппа ![]() (2m),
порождённая подгруппами T(2m) и P(2m)
группы
(2m),
порождённая подгруппами T(2m) и P(2m)
группы ![]() (2m),
совпадает с произведением подгрупп T(2m)P(2m)=
P(2m)T(2m)
и каждое преобразование
(2m),
совпадает с произведением подгрупп T(2m)P(2m)=
P(2m)T(2m)
и каждое преобразование ![]()
![]()
![]() (2m)
однозначно раскладывается в произведение инвертирующего и перестановочного преобразований
(2m)
однозначно раскладывается в произведение инвертирующего и перестановочного преобразований
![]() =
=![]()
![]() ,
или, столь же однозначно, - в произведение перестановочного и инвертирующего
преобразований
,
или, столь же однозначно, - в произведение перестановочного и инвертирующего
преобразований ![]() =
=![]() 1
1![]() 1,
где
1,
где ![]() ,
,![]() 1
1![]() T(2m)
и
T(2m)
и ![]() ,
,![]() 1
1![]() P(2m).
P(2m).
Доказательство:
1) То, что ![]() (2m)=
T(2m)P(2m)
следует (Курош,50) из перестановочности T(2m)P(2m)
= P(2m)T(2m).
Таким образом
(2m)=
T(2m)P(2m)
следует (Курош,50) из перестановочности T(2m)P(2m)
= P(2m)T(2m).
Таким образом ![]()
![]()
![]()
![]() (2m)
можно представить как произведения
(2m)
можно представить как произведения ![]() =
=![]()
![]() =
=![]() 1
1![]() 1,
где
1,
где ![]() ,
,![]() 1
1![]() T(2m)
и
T(2m)
и ![]() ,
,![]() 1
1![]() P(2m).
P(2m).
2) Если ![]() =
=![]() 1
1![]() 1=
1=![]() 2
2![]() 2,
то
2,
то ![]() 1=
1=![]() 2
и
2
и ![]() 1=
1=![]() 2.
Действительно, из
2.
Действительно, из ![]() 1
1![]() 1=
1=![]() 2
2![]() 2
следует
2
следует ![]() 1=
1=![]() 2
2![]() 2
2![]() 1-1
и
1-1
и ![]() 2-1
2-1![]() 1=
1=![]() 2
2![]() 1-1,
но левая часть этого равенства
1-1,
но левая часть этого равенства ![]() T(2m),
а правая часть
T(2m),
а правая часть ![]() P(2m)
и значит, по теореме 2,
P(2m)
и значит, по теореме 2, ![]() 2-1
2-1![]() 1=
1=![]() =
=![]() 2
2![]() 1-1,
поэтому
1-1,
поэтому ![]() 1=
1=![]() 2
и
2
и ![]() 1=
1=![]() 2.
2.
3) Аналогично, если ![]() =
=![]() 1
1![]() 1=
1=![]() 2
2![]() 2,
то
2,
то ![]() 1=
1=![]() 2
и
2
и ![]() 1=
1=![]() 2.
Действительно, из
2.
Действительно, из ![]() 1
1![]() 1=
1=![]() 2
2![]() 2
следует
2
следует ![]() 1=
1=![]() 1-1
1-1![]() 2
2![]() 2и
2и
![]() 1
1![]() 2-1=
2-1=![]() 1-1
1-1![]() 2,
но левая часть этого равенства
2,
но левая часть этого равенства ![]() T(2m),
а правая часть
T(2m),
а правая часть ![]() P(2m)
и значит, по теореме 2,
P(2m)
и значит, по теореме 2, ![]() 1
1![]() 2-1=
2-1=![]() =
=![]() 1-1
1-1![]() 2,
поэтому
2,
поэтому ![]() 1=
1=![]() 2
и
2
и ![]() 1=
1=![]() 2.
2.
Теорема 4.2.3:5: Число логических преобразований порядка 2m равно произведению числа инвертирующих преобразований порядка 2m и числа перестановочных преобразований порядка 2m, то есть 2m*m!.
Доказательство непосредственно следует из теоремы 4.
Теорема 4.2.3:6: Группа ![]() (2m)
имеет систему образующих из трёх преобразований:
(2m)
имеет систему образующих из трёх преобразований: ![]() 0=
0=
![]() (
(![]() 0),
0),
![]() 1=
1=
![]() (
(![]() 1)
и
1)
и ![]() 0=
0=![]() (1),
где
(1),
где
0=(m-2,m-1,...,3,2,0,1) - транспозиция чисел 0 и 1
1=(m-2,m-3,...,1,0,m-1) - циклический сдвиг всех элементов
Доказательство:
Поскольку ![]()
![]()
![]()
![]() (2m)
можно представить в виде произведения
(2m)
можно представить в виде произведения ![]() =
=![]()
![]() ,
где
,
где ![]()
![]() T(2m)
и
T(2m)
и ![]()
![]() P(2m),
и поскольку подгруппы T(2m) и P(2m)
имеют по теоремам 4.2.1:6 и 4.2.2:6
системы образующих, соответственно, {
P(2m),
и поскольку подгруппы T(2m) и P(2m)
имеют по теоремам 4.2.1:6 и 4.2.2:6
системы образующих, соответственно, {![]() i},
где i
i},
где i![]() I(m),
и {
I(m),
и {![]() 0,
0,![]() 1},
то эти две системы образующих в совокупности образуют систему {
1},
то эти две системы образующих в совокупности образуют систему {![]() i,
i,![]() 0,
0,![]() 1}
образующих
1}
образующих ![]() (2m).
(2m).
Легко показать, что ![]() i
i![]() I(m)
I(m)
![]() i=
i=![]() i
i![]() 0
0![]() i,
где
i,
где ![]() i
i![]() P(2m)
и
P(2m)
и ![]() (
(![]() i)=(m-1,m-2,...,i+1,0,i-1,...,2,1,i)
- транспозиция чисел 0 и i.
i)=(m-1,m-2,...,i+1,0,i-1,...,2,1,i)
- транспозиция чисел 0 и i.
Таким образом, ![]()
![]()
![]()
![]() (2m)
можно представить в виде произведений
(2m)
можно представить в виде произведений ![]() 0,
0,
![]() 1
и
1
и ![]() i,
где i
i,
где i![]() I(m);
далее, раскладываем
I(m);
далее, раскладываем ![]() i
для i>0 в произведение
i
для i>0 в произведение ![]() 0
и перестановочных преобразований; далее каждое перестановочное преобразование
раскладываем в произведение
0
и перестановочных преобразований; далее каждое перестановочное преобразование
раскладываем в произведение ![]() 0,
0,
![]() 1;
в результате
1;
в результате ![]() разложится в произведение трёх преобразований
разложится в произведение трёх преобразований ![]() 0,
0,
![]() 0,
0,
![]() 1.
Поэтому система образующих подгруппы
1.
Поэтому система образующих подгруппы ![]() (2m)
состоит из трёх преобразований:
(2m)
состоит из трёх преобразований: ![]() 0=
0=
![]() (
(![]() 0),
0),
![]() 1=
1=
![]() (
(![]() 1)
и
1)
и ![]() 0=
0=![]() (1).
(1).
Определение 4.3:1: Квадратом порядка n назовём матрицу nxn, элементы которой - это все числа из I(n2), то есть каждое целое число от 0 до n2-1 встречается как элемент матрицы и только один раз.
Очевидно, квадрат - это подстановка множества I(n2).
Обозначение 4.3:1: Множество квадратов порядка n обозначим K(n).
Очевидно, K(n)=![]() (n2).
(n2).
Обозначение 4.3:2: Если k![]() K(n)
и i,j
K(n)
и i,j![]() I(n),
то через k[i,j] обозначим число в i-ой строке и j-ом столбце квадрата
k, то есть, учитывая, что k - это подстановка множества I(n2),
k[i,j]=(ni+j)k.
I(n),
то через k[i,j] обозначим число в i-ой строке и j-ом столбце квадрата
k, то есть, учитывая, что k - это подстановка множества I(n2),
k[i,j]=(ni+j)k.
Определение 4.3.1:1: Набор n чисел из I(n2) назовём магическим, если сумма этих чисел равна (n2-1)n/2, то есть 1/n от суммы всех чисел из I(n2). Эта сумма (n2-1)n/2 называется магической и обозначается s(n).
Определение 4.3.1:2: Квадрат k![]() K(n)
назовём магическим (m-квадратом), если в нём каждая строка, каждый столбец и
каждая диагональ - магические, то есть имеют место равенства:
K(n)
назовём магическим (m-квадратом), если в нём каждая строка, каждый столбец и
каждая диагональ - магические, то есть имеют место равенства:
n-1 n-1 i
I(n)
k[i,j]=s(n) j
I(n)
k[i,j]=s(n) j=0 i=0 n-1 n-1 k[i,i]=s(n) k[i,n-1-i]=s(n) i=0 i=0
Обозначение 4.3.1:1: Множество m-квадратов порядка n обозначим M(n).
Определение 4.3.2:1: Набор n=2m чисел
xi![]() I(22m),
где i
I(22m),
где i![]() I(2m),
назовём равномерным, если в каждом двоичном разряде r
I(2m),
назовём равномерным, если в каждом двоичном разряде r![]() I(2m)
эти числа имеют поровну "1" и "0", то есть:
I(2m)
эти числа имеют поровну "1" и "0", то есть:
n-1 2m-1 r
I(2m)
xi|r = xi|r = n/2 = 2m-1 i=0 i=0
Определение 4.3.2:2: Квадрат k![]() K(2m)
назовём равномерным (r-квадратом), если в нём каждая строка, каждый столбец
и каждая диагональ равномерные, то есть
K(2m)
назовём равномерным (r-квадратом), если в нём каждая строка, каждый столбец
и каждая диагональ равномерные, то есть ![]() r
r![]() I(2m)
имеют место равенства:
I(2m)
имеют место равенства:
2m-1 2m-1 i
I(2m)
k[i,j]|r=2m-1 j
I(2m)
k[i,j]|r=2m-1 j=0 i=0 2m-1 2m-1 k[i,i]|r=2m-1 k[i,2m-1-i]|r=2m-1 i=0 i=0
Обозначение 4.3.2:1: Множество r-квадратов порядка 2m обозначим R(2m).
Определение 4.3.3:1: Два числа назовём симметричными порядка n, если их сумма равна n2-1=2s(n)/n.
Теорема 4.3.3:1: Симметричные числа порядка
2m взаимно-инвертированы, то есть если x+y=(2m)2-1=22m-1,
то x=![]() y.
y.
Доказательство очевидно.
Определение 4.3.3:2: Квадрат k![]() K(n)
назовём симметричным (c-квадратом), если в его центрально-симметричных клетках
находятся симметричные числа порядка n, то есть:
K(n)
назовём симметричным (c-квадратом), если в его центрально-симметричных клетках
находятся симметричные числа порядка n, то есть:
i,j
I(n) k[i,j]+ k[n-1-i,n-1-j]=n2-1.
Обозначение 4.3.3:1: Множество c-квадратов порядка n обозначим C(n).
Обозначение 4.3.3:2: Магические равномерные
симметричные квадраты будем называть s-квадратами. Множество s-квадратов порядка
2m обозначим S(2m)= M(2m)![]() C(2m)
C(2m)![]() R(2m).
R(2m).
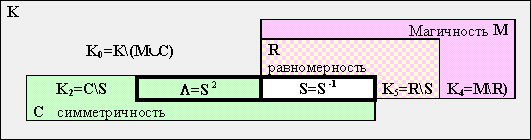
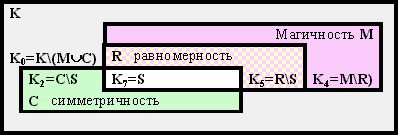
Формально 3 базовых свойства квадрата: магичность, равномерность и симметричность разбивают множество всех квадратов порядка 2m на 23=8 подмножеств Ki :
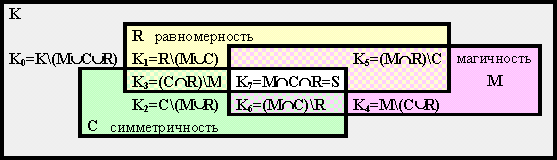
Мы покажем, что при m=2 только 5 из этих множеств непусты: K0=K\(M![]() C
C![]() R),
K2=C\(M
R),
K2=C\(M![]() R),
K4=M\(C
R),
K4=M\(C![]() R),
K5=(M
R),
K5=(M![]() R)\C,
K7=M
R)\C,
K7=M![]() C
C![]() R=S,
то есть R
R=S,
то есть R![]() M,
M
M,
M![]() C
C![]() R
и S=M
R
и S=M![]() C
C![]() R=M
R=M![]() C=C
C=C![]() R.
R.
| M=M(4) | C=C(4) | R=R(4) | S=S(4) |
| K=K(4)= |
T=T(16) | P=P(16) |
Обозначение 4.3.4:2: Шестнадцатиричные цифры будем обозначать так:
| 0= 010 | 1= 110 | 2= 210 | 3= 310 | 4= 410 | 5= 510 | 6= 610 | 7= 710 |
| 8= 810 | 9= 910 | A=1010 | B=1110 | C=1210 | D=1310 | E=1410 | F=1510 |
Теорема 4.3.4:1: Множество K0=K\(M![]() C
C![]() R)
непусто, то есть существует числовой квадрат 4-го порядка, не являющийся ни
магическим, ни равномерным, ни симметричным.
R)
непусто, то есть существует числовой квадрат 4-го порядка, не являющийся ни
магическим, ни равномерным, ни симметричным.
| Доказательство: |
|
Теорема 4.3.4:2: Множество K2=C\(M![]() R)
непусто, то есть существует симметричный квадрат 4-го порядка, не являющийся
ни магическим, ни равномерным.
R)
непусто, то есть существует симметричный квадрат 4-го порядка, не являющийся
ни магическим, ни равномерным.
| Доказательство: |
|
Теорема 4.3.4:3: Множество K4=M\(C![]() R)
непусто, то есть существует магический квадрат 4-го порядка, не являющийся ни
симметричным, ни равномерным.
R)
непусто, то есть существует магический квадрат 4-го порядка, не являющийся ни
симметричным, ни равномерным.
| Доказательство: |
|
Теорема 4.3.4:4: Множество K5=(M![]() R)\C
непусто, то есть существует магический равномерный квадрат 4-го порядка, не
являющийся симметричным.
R)\C
непусто, то есть существует магический равномерный квадрат 4-го порядка, не
являющийся симметричным.
| Доказательство: |
|
Теорема 4.3.4:5: Множество K7=M![]() C
C![]() R=S
непусто, то есть существует магический равномерный симметричный квадрат 4-го
порядка.
R=S
непусто, то есть существует магический равномерный симметричный квадрат 4-го
порядка.
| Доказательство: |
|
Квадрат Дюрера sd |
Теорема 4.3.4:6: Равномерный квадрат порядка
2m является магическим. Как следствие, R![]() M,
S=C
M,
S=C![]() R.
и множества K1=R\(M
R.
и множества K1=R\(M![]() C)
и K3=(C
C)
и K3=(C![]() R)\M
пусты.
R)\M
пусты.
Доказательство:
Учитывая разложение числа по степеням двойки (4.1), для
ряда (строки, столбца или диагонали) чисел xi, где i![]() I(2m),
любого квадрата k
I(2m),
любого квадрата k![]() K(2m)
можно записать:
K(2m)
можно записать:
2m-1 2m-1 2m-1 2m-1 2m-1 2m-1 2m-1 s = xi
= 2r*(xi|r) = 2r*(xi|r) = 2r
(xi|r)
i=0 i=0 r=0 r=0 i=0 r=0 i=0
| 2m-1 | |||
| Для равномерного квадрата |
имеет место равенство | = 2m-1 | |
| i=0 |
| 2m-1 | ||||
| Поэтому | s = | 2r*2m-1 = | (22m -1)*2m-1 = ((22m -1)*2m)/2 = s(2m) | |
| r=0 |
Теорема 4.3.4:7: Магический симметричный квадрат
4-го порядка является равномерным, то есть M![]() C
C![]() R,
S=M
R,
S=M![]() C
и множество K6=(M
C
и множество K6=(M![]() C)\R
пусто.
C)\R
пусто.
Вначале мы докажем три леммы.
Лемма 4.3.4:1: В симметричном магическом квадрате 4-го порядка числа "угловых" подквадратов образуют магический ряд:
| k[0,0] | k[0,1] | k[0,2] | k[0,3] |
|
||||||||||||||||||||||
| q0 | q1 | |||||||||||||||||||||||||
| k[1,0] | k[1,1] | k[1,2] | k[1,3] | |||||||||||||||||||||||
| k[2,0] | k[2,1] | k[2,2] | k[2,3] | |||||||||||||||||||||||
| q2 | q3 | |||||||||||||||||||||||||
| k[3,0] | k[3,1] | k[3,2] | k[3,3] |
Доказательство:
При повороте симметричного магического квадрата на 90o получается, очевидно, тоже симметричный магический квадрат. Поэтому лемму достаточно доказать для подквадрата q0. С учётом симметричности квадрата k его можно записать в виде (симметричные числа порядка 4 взаимно-инвертированы и их сумма равна F - теорема 4.3.3:1):
k[0,0] k[0,1] k[0,2] k[0,3] k[1,0] k[1,1] k[1,2] k[1,3] F- k[1,3] F- k[1,2] F- k[1,1] F- k[1,0] F- k[0,3] F- k[0,2] F- k[0,1] F- k[0,0]
Запишем условия магичности для строк 0,1 и столбцов 0,1 (для квадрата 4-го порядка s(4)=1E):
k[0,0] + k[0,1] + k[0,2] + k[0,3] = 1E k[1,0] + k[1,1] + k[1,2] + k[1,3] = 1E k[0,0] + k[1,0] + F- k[1,3] + F- k[0,3] = 1E k[0,1] + k[1,1] + F- k[1,2] + F- k[0,2] = 1E
Складывая эти равенства, получим:
2*( k[0,0] + k[0,1] + k[1,0] + k[1,1]) +4*F = 2*1E
Поэтому k[0,0] + k[0,1] + k[1,0] + k[1,1] = 1E, то есть лемма доказана для подквадрата q0.
Лемма 4.3.4:2: Диагонали симметричного квадрата 4-го порядка магичны.
Доказательство:
4 клетки диагонали квадрата - это две пары центрально-симметричных клеток. Поэтому на каждой диагонали находятся две пары симметричных чисел 4-го порядка. Сумма чисел каждой пары равна F и поэтому сумма всех четырёх чисел диагонали равна 1E, то есть магической сумме.
Лемма 4.3.4:3: Теорему 7 достаточно доказать для строки 0.
Доказательство:
Учитывая лемму 2, теорему 7 нужно доказывать для строк и столбцов. Доказательство леммы строится на том, что для каждой строки и каждого столбца существует преобразование квадрата, сохраняющее симметричность и магичность квадрата, и такое, что оно переводит эту строку или столбец в строку 0.
Для строки 3, столбцов 0 и 3 такое преобразование - это поворот квадрата на
180o, 90o и 270o по часовой стрелке, соответственно.
Для строки 1 это "перекрещивающее" преобразование вида (см. 3.3,
преобразование ![]() 13):
13):
|
|
k[0,0] k[0,1] k[0,2] k[0,3] k[2,0] k[2,1] k[2,2] k[2,3] |
строка 1 строка 0 строка 3 строка 2 столбец 1 столбец 0 столбец 3 столбец 2 |
Диагонали остаются на месте. | |||||||||||||||||||||||||||||||||||||||||||||
| Центрально-симметричные клетки переходят в центрально-симметричные клетки | ||||||||||||||||||||||||||||||||||||||||||||||||
Для строки 2 и столбцов 1 и 2 такое преобразование - это сочетание "перекрещивающего" преобразования и поворота по часовой стрелке на 180o, 90o и 270o, соответственно.
Доказательство теоремы 7:
Согласно лемме 3 будем доказывать равномерность строки 0.
1) Сначала докажем равномерность строки 0 для двоичного разряда 0, то есть, что в разряде 0 числа строки 0 имеют две "1" и два "0".
Поскольку магическая сумма 4-го порядка чётная (1E), числа любой строки (в том числе и строки 0) должны иметь в 0-м разряде чётное число "1": 0, 2 или 4. Допустим, что в 0-м разряде чисел строки 0 находятся 0 или 4 "1" и постараемся придти к противоречию.
Если в 0-м разряде чисел строки 0 четыре "1", то в строке 3, состоящей из клеток центрально-симметричных клеткам строки 0, числа имеют в 0-м разряде ноль "1" (все четыре "0"). Повернём квадрат на 180o и будем в новом симметричном магическом квадрате рассматривать строку 0. Итак, можно считать, что в строке 0 числа имеют в 0-м разряде все "0".
Числа строки 1 не могут иметь в 0-м разряде все "0", так как в противном случае мы получаем сумму всех восьми чётных чисел (в строках 0 и 1), равную удвоенной магической сумме 2*1E, а на самом деле она равна 0+2+4+6+8+A+C+E=2*1C.
Точно также числа строки 1 не могут содержать в разряде 0 все "1", так как тогда строка 2 как центрально-симметричная строке 1 состоит из чисел, имеющих в 0-м разряде все "0" и опять сумма всех восьми чётных чисел (в строках 0 и 2) оказывается равной 2*1E, что неверно.
Значит строка 1 содержит 2 чётных и 2 нечётных числа. Поскольку согласно лемме 1 сумма чисел в угловых подквадратах магическая, то есть чётна, очевидно строки 0 и 1 в 0-м разряде выглядят:
0000 или 0000 0011 1100
Из условия симметричности следует, что весь квадрат в 0-м разряде выглядит:
0000 или 0000 0011 1100 1100 0011 1111 1111
В обоих случаях на диагоналях получается нечётное число нечётных чисел, чего быть не может.
Итак, доказано, что числа строки 0 имеют в 0-м разряде две "1" и, соответственно, два "0".
2) При суммировании четырёх чисел строки 0, очевидно, будет перенос "1" в 1-ый разряд и, поскольку, магическая сумма 1E содержит "1" в 1-ом разряде, числа строки 0 должны иметь в 1-ом разряде чётное число "1": 0, 2 или 4.
Рассуждения для разряда 0 теперь полностью повторяются для разряда 1, так
как сумма всех восьми чисел, имеющих "0" в 1-ом разряде, равна 0+1+4+5+8+9+C+D=2*1A
![]() 2*1E.
2*1E.
3) Рассуждения для разряда 1 повторяются для разряда 2 с учётом того, что
сумма всех восьми чисел, имеющих "0" во 2-ом разряде, равна 0+1+2+3+8+9+A+B=2*16
![]() 2*1E.
2*1E.
4) Рассуждения для разряда 2 повторяются для разряда 3 с учётом того, что
сумма всех восьми чисел, имеющих "0" в 3-ем разряде, равна 0+1+2+3+4+5+6+7=2*10
![]() 2*1E.
2*1E.
Итак, теорема 7 доказана.
Каждое преобразование чисел ![]()
![]()
![]() (n)
естественно расширяется до преобразования квадратов
(n)
естественно расширяется до преобразования квадратов ![]() ':
K(n)
':
K(n)![]() K(n)
следующим образом:
K(n)
следующим образом: ![]() i,j
i,j![]() I(n)
k
I(n)
k![]() '[i,j]=
k[i,j]
'[i,j]=
k[i,j]![]() .
.
Говоря о преобразованиях чисел из ![]() (n2)
как преобразованиях квадратов, мы будем без специальных оговорок иметь
в виду такие расширения.
(n2)
как преобразованиях квадратов, мы будем без специальных оговорок иметь
в виду такие расширения.
Теорема 4.4.1:1: Расширение ' есть гомоморфизм
группы ![]() (n2)
преобразований множества I(n2) в группу преобразований множества
K(n)=
(n2)
преобразований множества I(n2) в группу преобразований множества
K(n)=![]() (n2)
по операции умножения преобразований:
(n2)
по операции умножения преобразований: ![]()
![]() ,
,![]()
![]()
![]() (n2)
(
(n2)
(![]()
![]() )'=
)'=
![]() '
'![]() '.
'.
Доказательство:
![]()
![]() ,
,![]()
![]()
![]() (n2)
(n2)
![]() i,j
i,j![]() I(n)
k(
I(n)
k(![]()
![]() )'[i,j]
= k[i,j](
)'[i,j]
= k[i,j](![]()
![]() )
= (k[i,j]
)
= (k[i,j]![]() )
)![]() = (k
= (k![]() '[i,j])
'[i,j])![]() = (k
= (k![]() ')
')![]() '[i,j]
= k(
'[i,j]
= k(![]() '
'![]() ')[i,j].
')[i,j].
Поскольку квадрат k порядка n - это преобразование (подстановка) множества
I(n2), то есть k![]()
![]() (n2),
то применение к числам квадрата k преобразования
(n2),
то применение к числам квадрата k преобразования ![]()
![]()
![]() (n2)
есть, фактически, умножение преобразований k
(n2)
есть, фактически, умножение преобразований k![]() :
:
![]() i,j
i,j![]() I(n)
( k[i,j])
I(n)
( k[i,j])![]() = (по обозначению 4.3:2) = ((ni+j) k)
= (по обозначению 4.3:2) = ((ni+j) k)![]() = (ni+j)(k
= (ni+j)(k![]() )
= (k
)
= (k![]() )[i,j].
)[i,j].
Преобразование ![]() клеток квадрата k
клеток квадрата k![]() K(n)
есть, фактически, преобразование множества индексов квадрата, то есть,
учитывая, что
K(n)
есть, фактически, преобразование множества индексов квадрата, то есть,
учитывая, что ![]() i,j
i,j![]() I(n)
[i,j]=(ni+j), множества I(n2). Тем самым
I(n)
[i,j]=(ni+j), множества I(n2). Тем самым ![]()
![]()
![]() (n2).
(n2).
В результате преобразования ![]() число
k[i,j] из клетки [i,j] переходит в клетку [i,j]
число
k[i,j] из клетки [i,j] переходит в клетку [i,j]![]() ,
то есть в новом квадрате k' будет k'([i,j]
,
то есть в новом квадрате k' будет k'([i,j]![]() )=
k[i,j].
)=
k[i,j].
k'([i,j]
) = k'((ni+j)
) = ((ni+j)
) k' = (ni+j)(
k')
k[i,j] = (ni+j)k
Поэтому (ni+j)(![]() k')
= (ni+j)k, то есть
k')
= (ni+j)k, то есть ![]() k'=
k и значит k'=
k'=
k и значит k'=![]() -1k.
-1k.
Пусть ![]() ,
,![]()
![]()
![]() (n2),
(n2),
![]() - это
преобразование чисел квадрата,
- это
преобразование чисел квадрата, ![]() - это преобразование клеток квадрата. Эти преобразования дают одинаковый результат
для квадрата k
- это преобразование клеток квадрата. Эти преобразования дают одинаковый результат
для квадрата k![]() K(n)=
K(n)=![]() (n2),
если, очевидно, k
(n2),
если, очевидно, k![]() =
=![]() -1k.
То есть
-1k.
То есть ![]() k
k![]() =k,
или
=k,
или ![]() =k-1
=k-1![]() -1k,
или
-1k,
или ![]() =k
=k![]() -1k-1.
-1k-1.
Теорема 4.4.5:1: Логические преобразования сохраняют
равномерность квадрата: ![]() k
k![]() R(2m)
R(2m)
![]()
![]()
![]()
![]() (2m)
k
(2m)
k![]()
![]() R(2m).
R(2m).
Доказательство:
Если квадрат порядка 2m равномерный, то каждая его строка, каждый столбец и каждая диагональ является равномерным набором чисел, то есть:
2m-1 r
I(2m)
xi|r = 2m-1, где i I(2m) и xi
22m
i=0
В силу теоремы 4.2.3:4 достаточно доказать теорему для инвертирующих и перестановочных преобразований.
В результате инвертирующего преобразования ![]() (t)
(t)![]() T(22m)
этот набор будет состоять из чисел xi
T(22m)
этот набор будет состоять из чисел xi![]() (t)=xi
(t)=xi![]() t
и соответствующая поразрядная сумма выглядит так:
t
и соответствующая поразрядная сумма выглядит так:
2m-1 2m-1 2m-1, если t|r=0 r
I(2m)
(xi t)|r =
(xi|r) (t|r) =
= 2m-1 2m-2m-1, если t|r=1 i=0 i=0
В результате перестановочного преобразования ![]() (
(![]() )
)![]() P(22m)
этот набор будет состоять из чисел xi
P(22m)
этот набор будет состоять из чисел xi![]() (
(![]() )
и соответствующая поразрядная сумма выглядит так:
)
и соответствующая поразрядная сумма выглядит так:
2m-1 2m-1 r
I(2m)
(xi (
))|r =
(xi|r ) = 2m-1
i=0 i=0
Теорема доказана.
Теорема 4.4.5:2: Логические преобразования сохраняют
симметричность квадрата: ![]() k
k![]() C(2m)
C(2m)
![]()
![]()
![]()
![]() (2m)
k
(2m)
k![]()
![]() C(2m).
C(2m).
Доказательство:
Нужно доказать, что логическое преобразование переводит два симметричных числа
порядка 2m в два симметричных числа того же порядка. В силу теоремы
4.2.3:4 достаточно доказать это для инвертирующих и
перестановочных преобразований. Согласно теореме 4.3.3:1
симметричные числа порядка 2m взаимно-инвертированы, то есть, если
x и y симметричны, то x=![]() y.
y.
В результате инвертирующего преобразования ![]() (t)
(t)![]() T(22m),
x
T(22m),
x![]() (t) = x
(t) = x![]() t
= (
t
= (![]() y)
y)![]() t
= (по теореме 4.1:1) =
t
= (по теореме 4.1:1) = ![]() (y
(y![]() t)
=
t)
= ![]() (y
(y![]() (t)).
(t)).
В результате перестановочного преобразования ![]() (
(![]() )
)![]() P(22m),
P(22m),
![]() r
r![]() I(2m)
(x
I(2m)
(x![]() (
(![]() ))|r
= (x|r
))|r
= (x|r![]() )
= (
)
= (![]() y|r
y|r![]() )
= (по определению 4.1:2) =
)
= (по определению 4.1:2) = ![]() (y|r
(y|r![]() )
=
)
= ![]() (y
(y![]() (
(![]() )).
)).
Теорема доказана.
Теорема 4.4.5:3: Каждый s-квадрат переводится
логическим преобразованием в s-квадрат: ![]() k
k![]() S(2m)
S(2m)
![]()
![]()
![]()
![]() (2m)
k
(2m)
k![]()
![]() S(2m).
S(2m).
Доказательство непосредственно следует из теоремы 4.3.4:7 и теорем 1,2.
Теорема 4.4.5:4: Если магический квадрат 4-го
порядка неравномерный, то существует логическое преобразование, переводящее
его в немагический квадрат: ![]() k
k![]() M\R
M\R
![]()
![]()
![]()
![]() k
k![]()
M.
Доказательство:
Пусть k![]() M\R.
Тогда существует ряд (строка, столбец или диагональ) чисел k0,k1,k2,k3
таких, что:
M\R.
Тогда существует ряд (строка, столбец или диагональ) чисел k0,k1,k2,k3
таких, что:
3 3 ki
= 1E и r
I(4) s(k)=
ki|r
2, то есть s(k)=0,1,3,4.
i=0 i=0
Пусть s(k)=0,1. В результате инвертирующего преобразования ![]() =
=![]() (F):
(F):
3 s(k )=
ki
|r
=4,3. Для s(k)=0,1,3,4. i=0
Пусть s(k![]() )=4.
В результате перестановочного преобразования, переводящего разряд r в разряд
3,
)=4.
В результате перестановочного преобразования, переводящего разряд r в разряд
3, ![]() =
=![]() (
(![]() ),
где
),
где
r,r1,r2,r3 , s(k ) =
3 =
ki |3 = 4, то есть
i
I(4) ki
8.
3,2,1,0 i=0
Поскольку ki![]()
![]() - это четыре разных числа, то s(k
- это четыре разных числа, то s(k![]()
![]() )
)![]() 8+9+A+B=2616>1E.
8+9+A+B=2616>1E.
Пусть теперь s(k![]() )=3.
В результате перестановочного преобразования, переводящего разряд r в разряд
0,
)=3.
В результате перестановочного преобразования, переводящего разряд r в разряд
0, ![]() =
= ![]() (
(![]() ),
где
),
где
r,r1,r2,r3 , s(k ) =
3 =
ki |0 = 3, то есть s(k
) - нечетна и значит не равна 1E.
0,3,2,1 i=0
Итак, мы доказали, что преобразование ![]()
![]() преобразует квадрат k в немагический квадрат.
преобразует квадрат k в немагический квадрат.
Теорема 4.4.5:5: R=R![]() ,
C=C
,
C=C![]() ,
S=S
,
S=S![]() ,
M
,
M![]() M
M![]() .
.
Доказательство:
Поскольку ![]() содержит тождественное преобразование, имеем:
содержит тождественное преобразование, имеем:
R
R
, C
C
, S
S
, M
M
.
Согласно теоремам 1,2,3,4, RR, C
C, S
S и M
\M
.
Поэтому R=R, C=C
, S=S
, M
M
.
Теорема 4.4.5:6: Подгруппа ![]() логических преобразований разбивает множества R, C, S на
непересекающиеся левосторонние смежные классы вида r
логических преобразований разбивает множества R, C, S на
непересекающиеся левосторонние смежные классы вида r![]() ,
c
,
c![]() ,
s
,
s![]() ,
где r
,
где r![]() R,
c
R,
c![]() C,
s
C,
s![]() S.
S.
Доказательство:
Сначала покажем, что ![]() разбивает всё множество квадратов K на непересекающиеся левосторонние
смежные классы (это известный факт теории групп).
разбивает всё множество квадратов K на непересекающиеся левосторонние
смежные классы (это известный факт теории групп).
Если a,b![]() K
и b
K
и b![]() a
a![]() ,
то
,
то ![]()
![]() 0
0![]()
![]() b=a
b=a![]() 0.
Тогда
0.
Тогда ![]()
![]() 1,
1,![]() 2
2![]()
![]() b
b![]() 1=a(
1=a(![]() 0
0![]() 1)
и a
1)
и a![]() 2=b(
2=b(![]() 0-1
0-1![]() 2),
то есть b
2),
то есть b![]() 1
1![]() a
a![]() и a
и a![]() 2
2![]() b
b![]() .
Поэтому два любых левосторонних смежных класса k
.
Поэтому два любых левосторонних смежных класса k![]() ,
где k
,
где k![]() K,
либо совпадают, либо не имеют общих элементов.
K,
либо совпадают, либо не имеют общих элементов.
Разложение множеств R, C, S на непересекающиеся левосторонние
смежные классы по подгруппе ![]() следует теперь из теоремы 5.
следует теперь из теоремы 5.
Теорема 4.4.5:7: Число левосторонних смежных
классов множества R равномерных квадратов 4-го порядка по подгруппе ![]() логических преобразований равно 11, а множества S симметричных равномерных
квадратов 4-го порядка - равно 1:
логических преобразований равно 11, а множества S симметричных равномерных
квадратов 4-го порядка - равно 1:
| ri и |
||
| i=0 |
Сначала мы докажем следующее утверждение:
Лемма 4.4.5:1: В любом равномерном квадрате 4-го порядка равномерными являются наборы чисел в подквадратах:
| "угловом" | - | k[0,0]+ k[0,3]+ k[3,0]+ k[3,3]=1E |
| "центральном" | - | k[1,1]+ k[1,2]+ k[2,1]+ k[2,2]=1E |
| "вертикально-среднем" | - | k[0,1]+ k[0,2]+ k[3,1]+ k[3,2]=1E |
| "горизонтально-среднем" | - | k[1,0]+ k[1,3]+ k[2,0]+ k[2,3]=1E |
Доказательство:
Пусть r![]() I(4).
I(4).
|
Рассмотрим картинку, на которой числом x (x=a,b,c,d) помечены клетки квадрата, в которых находят четыре числа x0,x1,x2,x3 такие, что | |||||||||||||||||
| 3 | ||||||||||||||||||
| i=0 |
Надо доказать, что a=b=c=d=2.
Запишем условия равномерности по разряду r для строк и столбцов квадрата:
| строки | 0,3: | a+b = 2*2 = 4 | столбцы | 1,2: | d+b = 2*2 = 4 | ||
| столбцы | 0,3: | a+c = 2*2 = 4 | строки | 1,2: | d+c = 2*2 = 4 | ||
| Отсюда: | 2a+(b+c) = 8 | 2d+(b+c) = 8 | |||||
Поэтому: 2a = 2d ![]() a = d
a = d
Условие равномерности по разряду r для диагоналей квадрата: a+d = 2*2 = 4. Поэтому
a= d = 2. Следовательно b= 4-a = 2, c = 4-a = 2.
Доказательство теоремы 7:
1) Для любого квадрата k![]() R
можно найти инвертирующее преобразование
R
можно найти инвертирующее преобразование ![]()
![]() T
такое, что k
T
такое, что k![]() [1,1]=F.
Действительно, для t(
[1,1]=F.
Действительно, для t(![]() )
=
)
= ![]() k[1,1],
k
k[1,1],
k![]() [1,1]
= k[1,1]
[1,1]
= k[1,1]![]() k[1,1]
=
k[1,1]
= ![]() ( k[1,1]
( k[1,1]![]() k[1,1])=
k[1,1])=
![]() 0 = F. Поэтому
далее будем рассматривать квадрат k1=k
0 = F. Поэтому
далее будем рассматривать квадрат k1=k![]() ,
в котором k1[1,1]=F.
,
в котором k1[1,1]=F.
2) Существует перестановочное преобразование ![]() 1
1![]() P
такое, что k1
P
такое, что k1![]() 1[2,2]
= 0,8,C,E.
1[2,2]
= 0,8,C,E. ![]() (
(![]() 1)
в зависимости от k1[2,2] определяется так:
1)
в зависимости от k1[2,2] определяется так:
| (3210): 0 |
(3210): 8 |
(3210): C |
(3210): E |
|||
| (2310): 4 |
(3120): A |
(3201): D |
||||
| (1230): 2 |
(3012): 9 |
(3012): B |
||||
| (0213): 1 |
(1230): 6 |
(0213): 7 |
||||
| (0213): 5 |
||||||
| (1032): 3 |
Поэтому далее будем рассматривать квадрат k2 = k1![]() 1,
в котором k2[2,2] = 0,8,C,E.
1,
в котором k2[2,2] = 0,8,C,E.
| 1 | 2 | 3 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
на главной диагонали две "1" в разряде 3 |
|
на главной диагонали две "1" в разрядах 3,2 |
|
на главной диагонали две "1" в разрядах 3,2,1 |
3) Существует перестановочное преобразование ![]() 2
2![]() P
такое, что центральный подквадрат в квадрате k3 = k2
P
такое, что центральный подквадрат в квадрате k3 = k2![]() 2,
с учётом его равномерности, имеет один из 12 типов. Квадрат k3
имеет вид:
2,
с учётом его равномерности, имеет один из 12 типов. Квадрат k3
имеет вид:
| 1.1 | 1.2 | 1.3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2.1 | 2.2 | 2.3 | 2.4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.1 | 3.2 | 3.3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4.1 | 4.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Рассмотрим все эти случае по порядку.
4) Квадрат k3 имеет вид:
| 1.1 | 1.3 | 4.1 | 4.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Условие равномерности ряда x,F,E,y: x+y=0+1. Числа, выделенные красным, уже есть в квадрате. Таким образом эти 4 случая отпадают. |
5) Квадрат k3 имеет вид:
| 2.1 | 2.4 | |||||||||||||||||||||||||||||||||
|
|
Условие равномерности ряда x,F,7,y: x+y=0+8. Числа, выделенные красным, уже есть в квадрате. Таким образом эти 2 случая отпадают. |
6) Квадрат k3 имеет вид:
| 1.2 | 3.1 | 3.3 | |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Условие равномерности ряда x,F,C,y: x+y=0+3=1+2. Значит, x=1, y=2 или x=2, y=1. |
Перестановкой ![]() 3
разрядов 1,0, не изменяющей уже имеющиеся в квадрате числа F,C,3,0, можно добиться
, чтобы в квадрате k3=k2
3
разрядов 1,0, не изменяющей уже имеющиеся в квадрате числа F,C,3,0, можно добиться
, чтобы в квадрате k3=k2![]() (
(![]() 3)
было x=2, y=1.
3)
было x=2, y=1.
| 1.2 | 3.1 | 3.3 | |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Условие равномерности ряда x,F,3,y: x+y=0+C=4+8. Числа, выделенные красным, уже есть в квадрате. Значит, x=4, y=8 или x=8, y=4. |
Перестановкой ![]() 4
разрядов 3,2, не изменяющей уже имеющиеся в квадрате числа F,C,3,2,1,0, можно
добиться , чтобы в квадрате k4=k3
4
разрядов 3,2, не изменяющей уже имеющиеся в квадрате числа F,C,3,2,1,0, можно
добиться , чтобы в квадрате k4=k3![]() (
(![]() 4)
было x=8, y=4.
4)
было x=8, y=4.
| 1.2 | 3.1 | 3.3 | |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Условие равномерности ряда x,3,0,y: x+y=F+C=E+D. Числа, выделенные красным, уже есть в квадрате. Значит, x=E, y=D или x=D, y=E. |
Для вариантов 3.1, 3.3 число "y" стоит в ряду, где уже есть два чётных числа 2,8. Поэтому y - нечётно, то есть x=E, y=D.
Для варианта 1.2 рассмотрим квадрат k|0 ( ![]() i,j
i,j![]() I(4)
(k|0)[i,j]=k[i,j]|0 ). v= k[0,0]|0, w=
I(4)
(k|0)[i,j]=k[i,j]|0 ). v= k[0,0]|0, w=![]() v,
t=y|0.
v,
t=y|0.
| 1.2|0 (0-й разряд квадрата 1.2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
равномерность столбца 2 |
|
равномерность столбца 0 |
|
равномерность столбца 3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таким образом y|0=t=1, то есть в варианте 1.2 тоже y - нечётно, и x=E, y=D.
| 1.2 | 3.1 | 3.3 | |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Условие равномерности ряда x,F,0,y: x+y=F+0=E+1=D+2=C+3=B+4=A+5=9+6=8+7. Числа, выделенные красным, уже есть в квадрате. Значит x=5, y=A или x=A, y=5 или x=9, y=6 или x=6, y=9. |
Число x стоит в ряду, в котором уже есть два чётных числа 2,E. Поэтому x - нечётно, то есть x=5, y=A или x=9, y=6.
| 1.2.1 | 1.2.2 | 3.1.1 | 3.1.2 | 3.3.1 | 3.3.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Достроим эти квадраты с помощью условий равномерности (или магичности). |
| 1.2.1 | 1.2.2 | 3.1.1 | 3.1.2 | 3.3.1 | 3.3.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Знаком "?" помечены клетки, в которых по условиям равномерности (магичности) должны быть записаны числа, уже имеющиеся в квадрате: 3,F. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| m0 | m1 | m2 | m3 | m4 |
Таким образом, первые 5 квадратов m0, m1, m2, m3, m4.
7) Квадрат k3 имеет вид:
| 2.2 | 2.3 | |||||||||||||||||||||||||||||||||
|
|
Условие равномерности ряда x,F,6,y: x+y=0+9=1+8. Числа, выделенные красным, уже есть в квадрате. Значит x=0, y=9 или x=9, y=0. |
Условие равномерности ряда u, 1, 8, z: u+z=F+6=E+7. Числа F, 6 уже есть в квадрате. Таким образом u=E, z=7 или u=7, z=E.
Рассмотрим для обоих вариантов 2.2, 2.3 квадраты k|0 ( ![]() i,j
i,j![]() I(4)
(k|0)[i,j]= k[i,j]|0). v=k[0,0]|0, w=
I(4)
(k|0)[i,j]= k[i,j]|0). v=k[0,0]|0, w=![]() v,
t=y|0, s=z|0.
v,
t=y|0, s=z|0.
| 2.2|0=2.3|0 (0-й разряд квадратов 2.2, 2.3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
равномерность столбцов 1, 2 |
|
равномерность строки 0 |
|
равномерность столбца 3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таким образом, y|0=t=v=s=z|0, то есть y и z одинаковой чётности. Поэтому x=0, y=9, u=E, z=7 или x=9, y=0, u=7, z=E.
| 2.2.1 | 2.2.2 | 2.3.1 | 2.3.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Условие равномерности ряда x,F,8,y: x+y=7+0=6+1=5+2=4+3. Числа, выделенные красным, уже есть в квадрате. Значит x=5, y=2 или x=2, y=5 или x=4, y=3 или x=3, y=4. |
Число x стоит в ряду, в котором уже есть два чётных числа 0,E. Поэтому x - нечётно, то есть x=5, y=2 или x=3, y=4.
Перестановкой ![]() 3
разрядов 2,1, не изменяющей уже имеющиеся в квадрате числа F,E,9,8,7,6,1,0 можно
добиться , чтобы в квадрате k3=k2
3
разрядов 2,1, не изменяющей уже имеющиеся в квадрате числа F,E,9,8,7,6,1,0 можно
добиться , чтобы в квадрате k3=k2![]() (
(![]() 3)
было x=5, y=2.
3)
было x=5, y=2.
| 2.2.1 | 2.2.2 | 2.3.1 | 2.3.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Условие равномерности ряда x,F,1,y: x+y=E+0=C+2=A+4=6+8. Числа, выделенные красным, уже есть в квадрате. Значит x=A, y=4 или x=4, y=A. |
Число x стоит в ряду, в котором уже есть два числа, имеющие "1" в разряде 2: 5|2=C|2=1. Поэтому x|2=0, то есть x=A, y=4.
| 2.2.1 | 2.2.2 | 2.3.1 | 2.3.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Таким образом, следующие 4 квадрата m5, m6, m7, m8 получены. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| m5 | m6 | m7 | m8 |
8) Квадрат k3 имеет вид:
| 3.2 | |||||||||||||||||
|
Условие равномерности ряда x,F,C,y: x+y=0+3=1+2. Условие равномерности ряда u,1,2,z: u+z=F+C=E+D. |
Рассмотрим квадрат k|0 ( ![]() i,j
i,j![]() I(4)
( k|0)[i,j]= k[i,j]|0). v=x|0, w=
I(4)
( k|0)[i,j]= k[i,j]|0). v=x|0, w= ![]() v,
s=u|0.
v,
s=u|0.
| 3.2|0 (0-й разряд квадрата) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
равномерность столбцов 1, 2 |
|
равномерность строки 0 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
Таким образом, x|0=v, u|0=s=w=![]() v,
то есть x и u разной чётности. Поэтому x=0, y=3, u=D, z=E или x=3, y=0, u=E,
z=D.
v,
то есть x и u разной чётности. Поэтому x=0, y=3, u=D, z=E или x=3, y=0, u=E,
z=D.
| 3.2.1 | 3.2.2 | |||||||||||||||||||||||||||||||||
|
|
Условие равномерности ряда x,3,E,y: x+y=D+0=C+1=9+4=5+8. |
Число x стоит в ряду, в котором уже есть два нечётных числа F,1. Поэтому x - чётно, то есть x=4, y=9 или x=8, y=5.
Перестановкой ![]() 3
разрядов 3,2, не изменяющей уже имеющиеся в квадрате числа F,E,D,C,3,2,1, можно
добиться , чтобы в квадрате k3=k2
3
разрядов 3,2, не изменяющей уже имеющиеся в квадрате числа F,E,D,C,3,2,1, можно
добиться , чтобы в квадрате k3=k2![]() (
(![]() 3)
было x=4, y=9.
3)
было x=4, y=9.
| 3.2.1 | 3.2.2 | |||||||||||||||||||||||||||||||||
|
|
Условие равномерности ряда x,F,2,y: x+y=D+0=C+1=9+4=5+8. |
Число x стоит в ряду, в котором уже есть два нечётных числа 3,D. Поэтому x - чётно, то есть x=8, y=5.
| 3.2.1 | 3.2.2 | |||||||||||||||||||||||||||||||||
|
|
Таким образом, следующие 2 квадрата m9, m10 получены. |
||||||||||||||||||||||||||||||||
| m9 | m10 |
9) Итак, мы получили 11 квадратов
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| m0 | m1 | m2 | m3 | m4 | m5 | m6 | m7 | m8 | m9 | m10 |
Сам способ их построения гарантирует, что они относятся к разным левосторонним
смежным классам множества R равномерных квадратов 4-го порядка по подгруппе
![]() логических
преобразований. Можно преобразовать их к виду, когда число 0 находится в клетке
[0,0], а числа 1,2,4,8 встречаются именно в таком порядке при считывании чисел
квадрата по строкам сверху вниз (в порядке возрастания [i,j]=4i+j). Очевидно,
что никакими логическими преобразованиями такие квадраты друг в друга перейти
не могут.
логических
преобразований. Можно преобразовать их к виду, когда число 0 находится в клетке
[0,0], а числа 1,2,4,8 встречаются именно в таком порядке при считывании чисел
квадрата по строкам сверху вниз (в порядке возрастания [i,j]=4i+j). Очевидно,
что никакими логическими преобразованиями такие квадраты друг в друга перейти
не могут.
ri = mi
(ti)
(
i)
| ti = | 5 | 2 | 2 | 2 | 2 | 5 | 2 | 5 | 2 | 3 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (1032) | (2310) | (3210) | (2031) | (3021) | (3012) | (0312) | (1302) | (1023) | (2310) | (2031) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| r0 | r1 | r2 | r3 | r4 | r5 | r6 | r7 | r8 | r9 | r10 |
10) Только один из этих одиннадцати квадратов является симметричным - квадрат
r0. Поэтому существует только один левосторонний смежный класс
множества S по подгруппе ![]() :
:
![]() s
s![]() S
s
S
s![]() =S.
=S.
Теорема 4.4.6:1: Логическое преобразование клеток
равномерного симметричного квадрата 4-го порядка переводит его также в равномерный
симметричный квадрат, то есть (согласно 4.4.3): ![]()
![]()
![]()
![]()
![]() s
s![]() S
S
![]() -1s
-1s![]() S.
S.
Доказательство:
1) Теорему достаточно доказать для одного (любого) s0![]() S.
Действительно, в силу теоремы 4.4.5:7
S.
Действительно, в силу теоремы 4.4.5:7 ![]() s
s![]() S
S
![]()
![]() 0
0![]()
![]() s=s0
s=s0![]() 0.
Поэтому, если
0.
Поэтому, если ![]()
![]()
![]()
![]() s1=
s1=![]() -1s0
-1s0![]() S,
то
S,
то ![]() -1s
=
-1s
= ![]() -1(s0
-1(s0![]() 0)
= (
0)
= (![]() -1s0)
-1s0)![]() 0
= s1
0
= s1![]() 0
0
![]() S.
S.
2) Поскольку ![]() имеет, согласно теореме 4.2.3:6, систему образующих
{
имеет, согласно теореме 4.2.3:6, систему образующих
{ ![]() 0,
0,
![]() 1,
1,
![]() 0},
где
0},
где ![]() (
(![]() 0)=
0)=![]() 0=(3201),
0=(3201),
![]() (
(![]() 1)=
1)=![]() 1=(2103),
t(
1=(2103),
t(![]() 0)=1,
то теорему достаточно доказать для
0)=1,
то теорему достаточно доказать для ![]() 0s0,
0s0,
![]() 1s0,
1s0,
![]() 0s0.
0s0.
Соответствующие им преобразования клеток, согласно 4.4.3,
![]() 0-1,
0-1,
![]() 1-1,
1-1,
![]() 0-1:
0-1:
(
0-1) =
0-1 =
0 = (3201)
(
1-1) =
1-1 = (0321)
t(0-1) = t(
0) = 1
 |
 |
 |
3) Для квадрата r0 из теоремы 4.4.5:7 имеем:
| r0 = |
|
|
|
|
Симметричность и равномерность (или магичность) этих квадратов проверяется непосредственно.
Теорема 4.4.6:2: Существует логическое преобразование
![]()
![]()
![]() клеток квадрата, которое каждый несимметричный квадрат ri
из теоремы 4.4.5:7 переводит в немагический квадрат,
то есть (согласно 4.4.3)
клеток квадрата, которое каждый несимметричный квадрат ri
из теоремы 4.4.5:7 переводит в немагический квадрат,
то есть (согласно 4.4.3) ![]() -1ri
-1riM.
Доказательство:
Рассмотрим преобразование ![]() 0,
0,
![]() 0(
0(![]() 0)=
0)=![]() 0=(3201).
Соответствующее ему преобразование клеток
0=(3201).
Соответствующее ему преобразование клеток ![]() 0-1=
0-1=![]() 0
переставляет местами столбцы 1 и 2. Для квадратов r1
0
переставляет местами столбцы 1 и 2. Для квадратов r1![]() r10
из теоремы 4.4.5:7 главная диагональ квадратов
r10
из теоремы 4.4.5:7 главная диагональ квадратов ![]() 0r1
0r1![]()
![]() 0r10
не является магической:
0r10
не является магической:
Теорема 4.4.6:3: Если равномерный квадрат 4-го
порядка не является симметричным, то существует логическое преобразование клеток,
переводящее его в неравномерный квадрат, то есть (согласно 4.4.3)
![]() r
r![]() R\S
R\S
![]()
![]()
![]()
![]()
![]() -1r
-1rR.
Доказательство:
1) В силу теоремы 4.4.5:7 теорему достаточно доказать
для любых представителей ri левосторонних смежных классов
R\ S по подгруппе ![]() .
.
Действительно, ![]() r
r![]() R
R
![]() i
i![]() I(11)
I(11)
![]()
![]() 0
0![]()
![]() r=ri
r=ri![]() 0.
0.
Поэтому, если ![]()
![]()
![]()
![]() k=
k=![]() ri
riR,
то
![]() r=
r=![]() (ri
(ri![]() 0)=(
0)=(![]() ri)
ri)![]() 0=k
0=k![]() 0.
0.
Очевидно, что k![]() 0
0R,
так как иначе, если k
![]() 0
0![]() R,
то (k
R,
то (k![]() 0)
0)![]() 0-1
0-1![]() R
и значит k
R
и значит k![]() R,
что неверно.
R,
что неверно.
2) В силу теоремы 2 теорема 3 доказана.
Теорема 4.4.6:4: Логическое преобразование клеток
симметричного квадрата 4-го порядка переводит его также в симметричный квадрат,
то есть (согласно 4.4.3) ![]() c
c![]() C
C
![]()
![]()
![]()
![]()
![]() -1c
-1c![]() C.
C.
Доказательство:
Достаточно проверить, что 3 преобразования клеток, соответствующие образующим
преобразованиям ![]() 0,
0,
![]() 1,
1,
![]() 0,
переводят центрально-симметричные клетки квадрата в центрально-симметричные
клетки. Это непосредственно видно по их схемам (доказательство теоремы
1).
0,
переводят центрально-симметричные клетки квадрата в центрально-симметричные
клетки. Это непосредственно видно по их схемам (доказательство теоремы
1).
Теорема 4.4.6:5: S=![]() S,
C=
S,
C=![]() C,
R=
C,
R=![]() R,
M
R,
M![]()
![]() M.
M.
Доказательство:
Поскольку ![]() содержит тождественное преобразование, имеем: S
содержит тождественное преобразование, имеем: S![]()
![]() S,
C
S,
C![]()
![]() C,
R
C,
R![]()
![]() R,
M
R,
M![]()
![]() M.
M.
Согласно теоремам 1![]() 4
4
![]() S
S![]() S,
S,
![]() C
C![]() C,
C,
![]() R
R![]() R,
R,
![]() M\M
M\M![]()
![]() .
.
Поэтому S=![]() S,
C=
S,
C=![]() C,
R=
C,
R=![]() R,
M
R,
M![]()
![]() M.
M.
Теорема 4.4.7:1: ![]() s
s![]() S
S
![]()
![]()
![]()
![]() s
s![]() =
=![]() s=S
s=S![]() =
=![]() S=S
S=S![]() =
=![]() S=S.
S=S.
Доказательство:
1) По теореме 4.4.5:7 ![]() s
s![]() S
s
S
s![]() =S.
Поскольку
=S.
Поскольку ![]() и S конечные множества, то число логических преобразований равно числу
s-квадратов.
и S конечные множества, то число логических преобразований равно числу
s-квадратов.
2) По теореме 4.4.5:5 S![]() =
S. По теореме 4.4.6:5
=
S. По теореме 4.4.6:5 ![]() S=S.
S=S.
3) Из 2) вытекает ![]() s
s![]() S
S
![]()
![]()
![]()
![]()
![]() s
s![]()
![]() S=S,
S
S=S,
S![]()
![]() S
S![]() =S,
=S,
![]() S
S![]()
![]() S=S.
В силу равномощности конечных множеств
S=S.
В силу равномощности конечных множеств ![]() и S имеем
и S имеем ![]() s=S
s=S![]() =
=![]() S=S.
S=S.
Доказательство:
1) Для квадрата Дюрера имеем
sd = sd-1 =
F 2 1 C 4 9 A 7 8 5 6 B 3 E D 0
2) Согласно теореме 4.4.5:7 ![]() s
s![]() S
S
![]()
![]()
![]()
![]() s=sd
s=sd![]() .
Поэтому s-1 = (sd
.
Поэтому s-1 = (sd![]() )-1
=
)-1
= ![]() -1sd-1
=
-1sd-1
= ![]() -1sd.
Согласно теореме 1, поскольку
-1sd.
Согласно теореме 1, поскольку ![]() -1
-1![]()
![]() ,
,
![]() -1sd
-1sd![]() S,
то есть s-1
S,
то есть s-1![]() S.
S.
3) Итак, S-1![]() S.
В силу конечности S имеем S-1=S
S.
В силу конечности S имеем S-1=S
Теорема 4.4.7:3: ![]() s
s![]() S
7е sS=Ss=S2=
S
7е sS=Ss=S2=![]() .
.
Доказательство:
1) ![]() s,s1
s,s1![]() S
s-1s1
S
s-1s1![]()
![]() .
.
Действительно, ![]() s,s1
s,s1![]() S
S
![]()
![]()
![]()
![]() ss1=s
ss1=s![]() .
Поэтому s-1s1=
.
Поэтому s-1s1=![]() ,
то есть s-1s1
,
то есть s-1s1![]()
![]() .
.
2) ![]() s,s1
s,s1![]() S
ss1
S
ss1![]()
![]() .
.
Действительно, ![]() s,s1
s,s1![]() S
ss1=(s-1)-1s1.
Согласно теореме 2 s-1
S
ss1=(s-1)-1s1.
Согласно теореме 2 s-1![]() S.
По 1) (s-1)-1s1
S.
По 1) (s-1)-1s1![]()
![]() ,
то есть ss1
,
то есть ss1![]()
![]() .
.
3) Из 2) следует, что ![]() s
s![]() S
sS
S
sS![]()
![]() ,
Ss
,
Ss![]()
![]() и
S2=SS
и
S2=SS![]()
![]() .
В группе всех преобразований K, как во всякой группе,
.
В группе всех преобразований K, как во всякой группе, ![]() s,s1,s2
s,s1,s2![]() S
S![]() K
s1
K
s1![]() s2
s2
![]() ss1
ss1![]() ss2
. Следовательно, поскольку множества sS, Ss и S конечные,
они имеют одинаковое число элементов. Поскольку, в свою очередь, число логических
преобразований равно числу s-квадратов, получаем, что sS=
ss2
. Следовательно, поскольку множества sS, Ss и S конечные,
они имеют одинаковое число элементов. Поскольку, в свою очередь, число логических
преобразований равно числу s-квадратов, получаем, что sS=![]() ,
Ss=
,
Ss=![]() и S2=SS=
и S2=SS=![]() .
.
Теорема 4.4.7:4: S![]()
![]() =S
=S![]() S2
является подгруппой группы k=
S2
является подгруппой группы k=![]() и это минимальная подгруппа, содержащая S.
и это минимальная подгруппа, содержащая S.
Доказательство:
1) S![]()
![]() =S
=S![]() S2
является подгруппой группы k=
S2
является подгруппой группы k=![]() :
:
По теореме 3: ![]()
![]()
![]() S
S
![]()
![]()
![]() S
S
![]()
![]()
![]()
![]() =S2.
=S2.
По теореме 1: ![]()
![]()
![]() S
S
![]()
![]()
![]()
![]()
![]()
![]()
![]() S.
S.
По теореме 1: ![]()
![]()
![]()
![]()
![]()
![]()
![]() S
S
![]()
![]()
![]() S.
S.
Поскольку ![]() подгруппа:
подгруппа: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =S2.
=S2.
По теореме 2: ![]()
![]()
![]() S
S
![]() -1
-1![]() S.
S.
Поскольку ![]() подгруппа:
подгруппа: ![]()
![]()
![]()
![]()
![]() -1
-1![]()
![]() =S2.
=S2.
2) Поскольку ![]() =S2,
то, очевидно, S
=S2,
то, очевидно, S![]()
![]() - минимальная подгруппа, содержащая S.
- минимальная подгруппа, содержащая S.
Теорема 4.4.7:5: Подгруппа S![]()
![]() =S
=S![]() S2
имеет систему образующих из четырёх преобразований { s0,
S2
имеет систему образующих из четырёх преобразований { s0, ![]() 0,
0,
![]() 1,
1,
![]() 0},
где
0},
где
s0 - любой симметричный магический квадрат (например, квадрат Дюрера sd),
(
0) = (3201),
(
1) = (2103),
t(0) = 1.
Доказательство непосредственно вытекает из теорем 4.2.3:6 и 4.4.5:7.
Теорема 4.4.7:6: Если логическое преобразование
16-го порядка рассматривать как квадрат 4-го порядка, то этот квадрат симметричен,
но не магичен, то есть ![]()
![]() C\M.
C\M.
Доказательство:
1) Поскольку по теореме 4.3.4:7 магический симметричный квадрат является равномерным, достаточно доказать, что логические преобразования симметричны и неравномерны.
2) Поскольку любое логическое преобразование можно представить как произведение
образующих преобразований ![]() 0,
0,
![]() 1,
1,
![]() 0
и поскольку логические преобразования сохраняют равномерность и симметричность
квадрата, то теорему достаточно доказать для этих преобразований.
0
и поскольку логические преобразования сохраняют равномерность и симметричность
квадрата, то теорему достаточно доказать для этих преобразований.
3) Симметричность и неравномерность преобразований ![]() 0,
0,
![]() 1,
1,
![]() 0
как квадратов 4-го порядка проверяется непосредственно:
0
как квадратов 4-го порядка проверяется непосредственно:
|
|
|
Теорема доказана.
Таким образом картинка квадратов 4-го порядка выглядит так: