 |
 |
 |
|
|
|
|
Число имеет много ипостасей. По-видимому, возникнув как порядковое число (первый, второй, третий,...), оно получило наибольшую формализацию как количественное число (один, два, три,...). Это видно уже из того, что только первые два числа в русском языке имеют разные корни для порядка и количества: первый-один, второй-два, а уже с числа 3 порядковое числительное образуется из количественного с помощью окончания: три-третий, четыре-четвёртый, пять-пятый,...
Для конечных чисел порядок и количество в известном смысле эквивалентны. Открытие кардинальных (бесконечных количественных) чисел и трансфинитных (бесконечных порядковых) чисел вновь явило их принципиальное различие: два разных трансфинитных числа могут соответствовать одному кардинальному числу. Но это в области бесконечного. На уровне языка (а не математики) порядковые и количественные числительные в Европе разделялись с самого начала. Выделялась и ещё одна ипостась числа - собирательное числительное (двое, трое,...).
Аналогично обстояло дело и в Китае. Однако, здесь же проявляются и различия. Артём Кобзев в книге "Учение о символах и числах в китайской классической философии" даёт следующую сравнительную таблицу для числа 2:
| числовые обозначения |
русский язык |
китайский язык |
| собирательные | двое | лян |
| количественные | два | эр |
| порядковые | второй | ди эр (букв. "по порядку - два") |
"Как показывает таблица, в европейских языках глубинное различие проходит между собирательными и количественными (в данном случае - однокоренными) числительными, с одной стороны, и порядковыми - с другой, что является лексическим коррелятом грамматическому различению множественного и единственного числа. Напротив, в китайском языке подобная граница отделяет количественные и производные от них порядковые обозначения чисел от собирательных, что отражает отсутствие грамматического различения множественного и единственного числа. Следовательно, на языковом уровне для китайской модели мира характерно разграничение не индивидов и множеств, а множеств и подмножеств, поскольку именно такое смыслоразличение осуществляется собирательными и количественными обозначениями чисел. Два - это подмножество какого-то более обширного множества (например, два человека из множества всех людей), а двое - самостоятельное множество. Показанная фундаментальная особенность китайского языка получила развитие в общеметодологической нацеленности китайских философов и учёных на осмысление мира как онтологической иерархии разного рода множеств и подмножеств."
Кобзев отмечает китайский "понятийный синкретизм единого и многого, чуждый того резкого их противопоставления, которое стало питательной средой для возникновения европейского идеализма и полемики вокруг проблемы универсалий." Примером служат понятия Дао и Великого Предела, обозначаемые одновременно и минимальным числом 1 (Единое) и "максимальным" числом 10.000 (множество всех вещей, что обычно переводится на русский как "вся тьма вещей").
Но что означает китайская "великая стена" между собирательными числительными и количественными и порядковыми числительными? Что означает "онтологическая иерархия" множеств и подмножеств?
Кобзев обращает внимание на ещё две особенности китайских чисел.
"Принципиальное различие между древнегреческим соматизмом и китайским процессуализмом, т.е. осмысление мира в образах дискретных тел, с одной стороны, и непрерывных процессов (событий, дел) - с другой." Этим объясняется разное отношение к иррациональным числам. "Фундаментальное открытие иррациональных чисел на основе установления несоизмеримости диагонали и стороны квадрата (или гипотенузы и катета равнобедренного прямоугольного треугольника) нанесло сокрушительный удар по числовой теории пифагорейцев и стимулировало геометризацию древнегреческой математики. Китайские же математики как будто не заметили качественной специфики иррациональных чисел, что, по мнению Дж. Нидэма, обусловливалось использованием ими десятичных дробей. В решении проблем, связанных с теоремой Пифагора, они ограничивались получением приближённых числовых значений и подбором троек пифагоровых чисел, т.е. целых числовых значений... В рамках китайского процессуализма, не знакомого ни с индивидуацией (букв. неделимостью) атомов, ни с индивидуацией идей (эйдосов), процессуализировавшего действительность и представляющего её в виде множества континуальных масс, бесконечная десятичная дробь вполне могла пониматься как отражение бесконечной делимости любого материального предмета или явления и потому не казалась чем-то необычайным."
Эта "процессуальность" китайской математики делала её более алгебраичной. Однако, спор об алгебраичности или геометричности китайской математики и шире - китайского способа мышления - вовсе не закончен. Разные исследователи придерживаются противоположных точек зрения. В пользу алгебраичности, помимо отношения к иррациональным числам, говорит вся китайская нумерология с её "алгебраическими" операциями над триграммами, гексаграммами, пятью элементами и собственно числами. Здесь выделяются целые классы различных преобразований, а, кстати, современная алгебра возникла из теории групп, которая, в свою очередь, начинала развиваться именно как теория преобразований (группы Галуа). Манипуляции со всевозможными последовательностями пяти элементов напоминают о группе подстановок степени 5. Сам способ построения китайских нумерологических чисел из базовых чисел 1,2,3 и 5 (впрочем, число 5 часто тоже строилось как 2+3) с помощью арифметических операций сложения, умножения и возведения в степень есть способ алгебраический именно в современном его понимании, когда некоторое подмножество элементов с помощью определённых алгебраических операций расширяется до полной (в смысле этих операций) алгебраической структуры.
И, тем не менее, следует признать, что китайским числам геометричность присуща никак не меньше, чем алгебраичность.
Согласно китайской традиции числа рисовались состоящими из соответствующего
количества кружков: белых (нечётные) и чёрных (чётные). В "Цзо чжуани"
(Y-IY вв. до н.э.) сказано: "Рождаются вещи, а затем возникают символы
(визуальные геометрические образы); вслед за символами возникает размножение;
вслед за размножением возникают числа." В древнейшем математическом каноне
"Чжоу би" говорится: "Законы чисел исходят из круглого и квадратного",
- т.е. числа объявляются производными от геометрических образов. Геометричность
видна и в тесной связи чисел с чертами триграмм и гексаграмм (3 и 9 - целая
черта ян 
, 2 и 6 - прерванная черта
инь 
), с самими триграммами и гексаграммами.
Основополагающие нумерологические матрицы - квадрат Ло Шу и крест Хэ Ту - являются
одновременно числовыми и геометрическими конструкциями.
Мне кажется, китайская нумерология демонстрирует две новые ипостаси числа, отличные как от количества, так и от порядка.
Первую ипостась я бы назвал "алгебраическим" числом. Это такие числа, которые определяются через операции над числами. Суть алгебраического числа не в том, что оно обозначает количество или порядок, в а том, что над ним можно выполнять различные алгебраические операции. Алгебраическое число - это такая абстракция общей идеи числа, когда мы отвлекаемся не только от предметов, которые считаются, но и от понятий количества и порядка, и интересуемся только операциями над числами. Примерами таких операций являются, конечно, обычные арифметические операции сложения, умножения и т.п. По существу алгебраическая ипостась числа породила всю современную алгебру, базирующуюся на теории групп. Алгебраические числа - как бы даже уже не числа, а просто какие-то элементы множества, над которыми определены некоторые операции с определёнными свойствами (ассоциативность, коммутативность, дистрибутивность и т.д.).
В китайской нумерологии зародыши таких операций просматриваются в манипулировании самыми разными нумерологическими элементами: триграммами, гексаграммами, пятью элементами, элементами 60-летнего цикла, направлениями пространства (4,6 или 8 сторон света), делениями времени суток, года, жизни человека и т.п. Все эти элементы вроде бы не числа, но китайская традиция всегда связывает с ними числа и, таким образом, сами числа также оказываются вовлечёнными в необычные (неарифметические) операциями с ними.
По-видимому, алгебраическое число соответствует собирательному числительному. Действительно, алгебраичность числа смещает акцент с самого отдельного числа на операции над числами. Алгебраично всегда множество чисел: группа, кольцо, поле и т.п. Именно множеству чисел соответствует собирательное числительное. В алгебре особое внимание уделяется "иерархии подмножеств": подгруппы, разложение на смежные классы по операциям, прямые произведения и т.д.
Иерархия подмножеств тесно связана с логикой, а именно с булевой алгеброй. Одна из первых и наиболее распространённых и "понятных" интерпретаций логических операций - их интерпретация через операции на множествах: дизъюнкция = объединение множеств, конъюнкция = пересечение множеств, отрицание = дополнение множества и т.д.
Собирательные числительные в европейских языках слабо развиты. Во многих словарях
(например, "Советский энциклопедический словарь", М.,1983; "Словарь
русского языка" С.И. Ожегова, М.,1987) числительное определяется только
как количественное или порядковое, но зато указывается собирательное существительное,
"форма единственного числа которых обозначает совокупность лиц, одинаковых,
однородных или сходных предметов (листва, молодняк) как одно неделимое целое".
По семантике такими собирательными существительными являются слова "библиотека",
"фонотека", "дискотека" (в смысле собрания "дисков",
а не танцзал), образованные от "-тека" (греческое 
- хранилище). Например, библиотека - это не просто собрание книг, но собрание
определённым образом организованное, каталогизированное; в библиотеке есть библиотекари
и читатели, они определённым образом функционируют, выполняются операции выдачи
и приёма книг, поиска и т.п. То есть библиотека - это своего рода алгебраическая
структура.
Вторая ипостась числа более интересная - это "структурное" число. Здесь число выступает не как количество чего-либо, не как номер чего-либо и не как операнд алгебраических операций, а как самостоятельный объект, определённым образом организованный, имеющий внутреннюю структуру.
По-видимому, в Европе понимание числа как структуры впервые появилось вместе с изобретением позиционной системы счисления. Действительно, про число 125 мы можем сказать, что оно имеет три десятичных разряда (единицы, десятки и сотни) и эти разряды заняты цифрами 1,2 и 5. Число становится структурой - вектором, линейной последовательностью цифр. Числа 69 и 96 кажутся нам ассоциированными друг с другом только потому, что оба они имеют два разряда и состоят из одних и тех же цифр 6 и 9. В другой системе счисления, например, в восьмеричной, они записываются иначе - 105 и 140, и уже не кажутся похожими.
Дробные числа имеют более сложную структуру: представление в виде десятичной
дроби содержит ещё один элемент структуры - десятичную точку (например, 125.69).
Введение отрицательных чисел добавляет ещё один элемент структуры - знак ("+"
или "-"). Особую структуру имеет представление числа с плавающей запятой
N= 
Rp*q,
где R - выбранное основание (обычно, 10), p - порядок (целое число) и q - мантисса
числа N, обычно являющаяся правильной дробью (1/R
0q<1).
В этом представлении структура числа состоит из элементов: знак порядка, знак
числа, цифровой код порядка и цифровой код мантиссы. Это представление является
основным способом для ЭВМ, так как позволяет поддерживать вычисления с сохранением
заданного числа значащих цифр в большом диапазоне значений числа. (Основание,
как правило, выбирается двоичное R=2.)
В вычислительной технике и программировании основной стала двоичная система счисления, имеющая только две цифры "0" и "1". Прежде всего, это связано с особенностями электронных элементов и электрических сигналов: "0" - сигнала нет, "1" - сигнал есть. Более глубокая связь - с двоичной логикой: "0" - ложь, "1" - истина. По-существу, вычислительная машина - это "логическая" машина, имеющая дело со множеством двоичных переменных (триггеров, хранящих значения "0" или "1") и логическими операциями над ними (конъюнкция, дизъюнкция, отрицание и т.п.). Арифметические операции - более сложные и для их выполнения используются специальные алгоритмы, "зашитые" в аппаратные схемы машины. Единственной "простой" операцией (кроме логических) является операция сдвига двоичного кода влево (или вправо) на один разряд, т.е. умножение (или деление) на 2.
Производными от двоичной системы счисления являются используемые в программировании восьмеричная и шестнадцатиричная системы счисления. Их удобство (и вообще системы счисления с основанием, равным степени двойки) заключается в тривиальности преобразования в двоичную систему и обратно: каждая восьмеричная (шестнадцатиричная) цифра преобразуется стандартно в три (четыре) двоичных разряда независимо от её позиции. Имея таблицу двоичных кодов восьмеричных (шестнадцатиричных) цифр, такие преобразования делать очень легко.
| восьмеричная цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||||||
| двоичный код | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 | ||||||||
| шестнадцатиричная цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| двоичный код | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
1258 = 001 010 101 = 8510 12516 = 0001 0010 0101 = 29310
Иными словами, двоичный код восьмеричного (шестнадцатиричного) числа есть просто последовательность двоичных кодов составляющих число восьмеричных (шестнадцатиричных) цифр. Таким образом, базовыми оказываются двоичные коды цифр. Эти коды представляют собой структуры из "0" и "1". Восьмеричные цифры - это все возможные тройки из "0" и "1", шестнадцатиричные цифры - это все возможные четвёрки из "0" и "1".
С двоичной структурой чисел связаны все операции над ними. Логические операции определяются поразрядно, например:
| 1258 & 638 = 218 | 1258 | = | 001 010 101 | |
| 638 | = | 000 110 011 | ||
 |
||||
| 218 | = | 000 010 001 |
Операция сравнения (больше, меньше) определяет из двух двоичных кодов тот, в котором единицы "самые левые". Например, из двух чисел 638 и 658 второе число больше, потому что в двоичных кодах этих чисел при самом левом несовпадении значений разрядов у числа 638 в этом разряде стоит "0", а у числа 658 - "1":
638 = 110 20 011
658 = 110 21 001
Двоичные коды используются в ЭВМ и программировании не только для представления чисел, но и для кодирования любой информации. В частности, восьмиразрядными двоичными кодами (две шестнадцатиричные цифры) обозначаются все буквы и знаки. Каждая буква или знак при выбранной кодировке оказывается связанной с парой шестнадцатиричных цифр, т.е. с числом от 0 до 255. В ЭВМ всё оказывается числами, но эти числа часто уже не выражают идеи количества или порядка. Они выражают идею кода, то есть двоичной структуры.
У человека, знакомого с программированием или просто с двоичной системой счисления, китайские инь и ян - мгновенно ассоциируются с "0" и "1", триграммы как все возможные тройки двух видов черт - с восьмеричными цифрами, гексаграммы - с парами восьмеричных цифр. Не случайно Лейбниц, занимавшийся двоичной системой счисления, когда ознакомился с гексаграммами "И ЦЗИНа", пришёл в восхищение и послал китайскому императору письмо, в котором убеждал его, что 64 гексаграммы - это закодированный гиперкуб (куб шестимерного пространства). Борхес даже считал наоборот, что гексаграммы "И ЦЗИНа" подвигли Лейбница на изобретение двоичной системы счисления.
Точно также пять элементов, девять цифр квадрата Ло Шу, девять чисел креста Хэ Ту - это тоже коды, но, правда, уже не двоичной структуры.
Глубинное тождество шестнадцатиричных цифр и логических операций, основанное на двоичном кодировании логических операций, существенно связано со структурной ипостасью числа. Именно в этой ипостаси число 3 это код 0011, а число 5 это код 0101, то есть они соответствуют операндам x и y в кодировке логических функций (выбор кодировки x=0011, y=0101 не единственно возможный, но об этом ниже).
Число 7 это код 0111, что соответствует дизъюнкции:
x = 0011 y = 0101 x y
= 0111
Число 1 это код 0001, что соответствует конъюнкции:
x = 0011 y = 0101 x&y = 0001
В силу такого способа кодировки логические операции над цифрами, применяемые поразрядно, дают тот же результат, что взятие двоичного кода производной логической операции. Например:
(x (x&y)
x
0y
код (x
70111 0001 1001
Более того, поскольку код импликации ()
равен D, можно записать 7D1=9 или, в функциональной нотации, D(7,1)=9.
Таким образом, каждая шестнадцатиричная цифра определяет соответствующую логическую операцию, которая применяется к цифрам - операндам поразрядно. Структурная цифра есть одновременно и число в обычном понимании и операция над числами. Таблицы этих операций приведены в Приложении 1.
Логический смысл теории базируется на структурных числах, на тождестве шестнадцатиричных цифр и логических операций. Базовые понятия теории числовых квадратов 4-го порядка, как показано в разделе 4, - это симметричность и равномерность квадратов, инвертирующие и перестановочные преобразования (логические преобразования). В этом подразделе укажем на логический смысл этих понятий, то есть на их смысл, когда числа понимаются как логические операции. В основном об этом уже шёл предварительный разговор в разделе 3. Здесь мы подводим итоги и проводим нумерологический анализ полученных результатов.
Симметричный квадрат чисел - это квадрат, центрально-симметричные клетки которого занимает пара симметричных чисел a и b, то есть таких, что a+b=F16.
Если a и b - это коды логических функций, то равенство a+b=F эквивалентно
a=
b (или b=a).
Иными словами, симметричный квадрат операций - это квадрат, центрально-симметричные
клетки которого занимает пара взаимно-инвертированных операций, то есть таких,
что каждая операция есть отрицание другой операции пары. В этом и состоит логический
смысл симметричности.
В китайской нумерологии при квадратно-круговом расположении триграмм и гексаграмм взаимосвязь через центр называется принципом сян цо.
Коды взаимно-инвертированных операций поразрядно противоположны. Например,
конъюнкция x&y имеет двоичный код 0001, а её отрицание, штрих Шеффера, x
y
= (x&y) -
код 1110. Это соответствует почертной противоположности-супротивности - сян
дуй, пан тун триграмм и гексаграмм. Например, триграммы:
ГРОМ ДЕРЕВО
Эти два принципа сян цо и сян дуй соответствуют сянь тянь - "преднебесному", то есть первоприродному, генотипическому, априорному. Этому соответствует древнейшее расположение триграмм и гексаграмм, приписываемое императору Фу Си. В расположении триграмм по периферии 9-клеточного квадрата по Фу Си центрально-симметричные клетки заняты взаимно-противоположными триграммами:
дуй
озеро
цянь
небо
сюнь
ветер
ли
огонь
кань
вода
чжэнь
гром
кунь
земля
гэнь
гора
Можно ли сделать какие-то выводы из этого соответствия отрицания и "преднебесного"? По-видимому, это говорит о фундаментальной природе отрицания, более фундаментальной, чем другие логические операции, лежащие в основе равномерности квадрата.
Равномерный квадрат чисел - это квадрат, в каждом ряду (строке, столбце, диагонали) которого четыре числа имеют в каждом из четырёх разрядов поровну (по две) "1" и "0". Уже само определение равномерности требует представления числа как двоичной структуры.
Если четыре числа a,b,c,d - это коды логических операций, то условие равномерности можно записать в виде:
a & b & c & d a & b & c d a & b & c & d a & b & c & d a & b & c d a & b & c & d = F16
Однако, более интересно следующее эквивалентное условие. Рассмотрим те из 16
логических операций, которые одновременно ассоциативны и коммутативны. Таких
операций четыре: конъюнкция &, дизъюнкция ,
эквивалентность
и исключающая дизъюнкция 
.
Квадрат равномерный тогда и только тогда, когда для каждого ряда:
a&b&c&d = 0 a a a
Действительно, легко показать, что:
a&b&c&d = 0 в каждом разряде есть "0" ( число "1" < 4 ); a в каждом разряде есть "1" ( число "1" > 0 ); a в каждом разряде число операндов, равных "1", равно по модулю 2 общему числу операндов; для 4-х операндов это означает, что число "1" чётно. a
Как видно, два последних условия эквивалентны.
Итак, все 4 условия выполняются тогда и только тогда, когда число "1" в каждом разряде меньше 4, больше 0 и чётно, то есть равно 2.
Проверка равномерности по рядам чисел, быть может, соответствует взаимосвязи триграмм и гексаграмм по периметру или окружности при квадратно-круговом расположении (принцип сян цзун).
Взаимная перевёрнутость-обратность - фань дуй, цянь гуа - триграмм
и гексаграмм, быть может, связана с равномерностью в том смысле, что равномерность
ряда из 4-х логических операций инвариантна к переворачиванию кодов всех 4-х
логических операций ряда (например, 1011 
1101).
Эти два принципа ( сян цзун и фань дуй) соответствуют хоу тянь - "посленебесному", то есть природоявленному, фенотипическому, апостериорному. Этому соответствует более позднее расположение триграмм и гексаграмм, приписываемое Вэнь-вану. В расположении гексаграмм по Вэнь-вану пара соседних гексаграмм (гексаграмма с нечётным и следующим за ним чётным номерами) - это взаимно-перевёрнутые гексаграммы, например:
|
|
И только если переворачивание не меняет гексаграмму, вступает в действие принцип противоположности-супротивности - сян дуй, например:
|
|
Всякое преобразование, названное в разделе 4 "логическим", может быть представлено (и единственным образом!) как произведение (последовательное выполнение) двух преобразований: инвертирующего и логического. Эти преобразования существенно опираются на структурное представление чисел.
Инвертирующее преобразование чисел меняет некоторые двоичные разряды на противоположные. Для логических операций это означает применение исключающей дизъюнкции с тем или иным вторым операндом. 16 инвертирующих преобразований - это все преобразования вида:
(p) = p
где t пробегает все логические функции.
Для триграмм и гексаграмм это соответствует почертной противоположности-супротивности
сян дуй, пан тун. Такая полная противоположность есть частный
случай инвертирующего преобразования, когда t=F (тождественно истинная логическая
функция), то есть когда инвертирующее преобразование меняет все двоичные разряды
числа (кода логической функции) на противоположные, что для логической операции
означает её отрицание: pF
= p. Инвертирующее
преобразование - "преднебесное".
Перестановочное преобразование чисел меняет порядок следования двоичных разрядов. Для логических операций это означает подстановку в качестве операндов операции вместо x и y тех или иных логических операций a и b. 24 перестановочных преобразований - это все преобразования вида:
(p) = p(a,b), то есть
где a и b пробегают все логические операции такие, что a&b0, a
b
Для триграмм и гексаграмм это соответствует взаимной перевёрнутости-обратности - фань дуй, цянь гуа. Такая перевёрнутость есть частный случай перестановочного преобразования. p(a,b) есть "перевёрнутое" p, в зависимости от p для нескольких пар a и b. В таблице операций (Приложение 1) перевёрнутые коды логических операций выделены белым шрифтом на черном фоне. Перестановочное преобразование - "посленебесное".
До сих пор мы изучали исключительно бинарные, унарные и нуль-арные (тождественные истина и ложь) логические операции. Унарная (нуль-арная) операция - частный случай функции от 2-х переменных, когда один из аргументов (оба аргумента) не влияет на значение функции. То есть мы изучали все 16 логических функций от 2-х переменных. Является ли это ограничением? Нет, поскольку известно, что в логическом смысле существенны логические функции именно от 2-х переменных: всякую логическую функцию от n>2 переменных можно выразить через логические функции от 2-х переменных.
Действительно, пусть f(x1,x2,...xn-1,xn) - логическая функция от n>2 переменных.
Обозначим: fi(x1,x2,...xn-1) = f(x1,x2,...xn-1,i), где i=0
F
F Тогда, очевидно, f = (fi& i=0
Функции fi - логические функции от n-1 переменных. Применяя тот
же приём к этим функциям, и так далее, получим в конце концов выражение f через
функции от 2-х переменных (включая операции &, ,
).
Числа 3 и 5 являются важнейшими в китайской нумерологии. Достаточно отослать к 4-ой главе книги Кобзева "Учение о символах и числах в китайской классической философии", которая так и называется "Универсальная троично-пятеричная модель мироздания". Следует подчеркнуть, что по нумерологическим правилам 3 и 5 являются репрезентантами целого класса чисел: 3=6,9,12,18,27,81,... и 5=10,25,50,100,125,...
Числа 3 и 5 оказываются также важнейшими в числовой булевой алгебре B16 (в которой аргументы и операции - шестнадцатиричные цифры). На них основана кодировка логических операций: пары возможных значений аргументов x и y перечисляются в порядке:
(0,0), (0,1), (1,0), (1,1) или, в иной записи:
x = 0011 = 3
y = 0101 = 5
3 и 5 оказываются числовыми кодами функций 3(x,y)=x и 5(x,y)=y.
Возникает, однако, вопрос: не является ли это случайностью? Быть может, при другом перечислении пар возможных значений аргументов получатся совсем другие числа? Рассмотрим эти иные способы кодировки. Кодировка будет допустимой, если в перечислении присутствуют все четыре разные возможные пары. Иными словами, при любой правильной кодировке:
r3,r2,r1,r0
I(4) такие, что
xr3=0 xr2=0 xr1=0 xr0=0 yr3=0 yr2=0 yr1=0 yr0=0
Всего получается 24 возможные кодировки.
x y |
в этих графах десятичные числа | |||
3 5 |
3 * 5 |
3*5 |
3 *(3 + 2) |
15 |
3 6 |
3 * 6 |
3*3*2 |
3 * 3 * 2 |
18 |
3 9 |
3 * 9 |
3*3*3 |
3 * 3 * 3 |
27 |
3 A |
3 * 10 |
3*5*2 |
3 *(3 + 2)* 2 |
30 |
5 3 |
3 * 5 |
|||
5 6 |
5 * 6 |
3*5*2 |
3 *(3 + 2)* 2 |
30 |
5 9 |
5 * 9 |
3*3*5 |
3 * 3 *(3 + 2) |
45 |
5 C |
5 * 12 |
3*5*2*2 |
3 *(3 + 2)* 2 * 2 |
60 |
6 3 |
6 * 3 |
|
|
|
6 5 |
6 * 5 |
|||
6 A |
6 * 10 |
3*5*2*2 |
3 *(3 + 2)* 2 * 2 |
60 |
6 C |
6 * 12 |
3*3*2*2*2 |
3 * 3 * 2 * 2 * 2 |
72 |
9 3 |
9 * 3 |
|||
9 5 |
9 * 5 |
|||
9 A |
9 * 10 |
3*3*5*2 |
3 * 3 *(3 + 2)* 2 |
90 |
9 C |
9 * 12 |
3*3*3*2*2 |
3 * 3 * 3 * 2 * 2 |
108 |
A 3 |
10 * 3 |
|||
A 6 |
10 * 6 |
|||
A 9 |
10 * 9 |
|||
A C |
10 * 12 |
3*3*5*2*2 |
3 * 3 *(3 + 2)* 2 * 2 |
120 |
C 5 |
12 * 5 |
|||
C 6 |
12 * 6 |
|||
C 9 |
12 * 9 |
|||
C A |
12 * 10 |
|||
В таблице приведены значение и структура произведения кодов x и y для каждого варианта. Пары операндов, отличающиеся только порядком операндов (x,y и y,x), расположены в строках с разным цветом фона (серый фон для x<y). Как легко видеть, все варианты базируются на числах 3 и 5 (а также 2). Поскольку 5=3+2, можно представить все варианты как структуры, основанные на числах 2 и 3.
Числа 3 и 5, также как любая другая возможная пара, обладают следующими свойствами, если их рассматривать как структурные числа:
Это определение эквивалентно приведённому выше определению правильной кодировки. Оно явно опирается на структурность чисел. Отсюда же следует, что пара 2 и 3 не обладает этими свойствами. Таким образом, хотя 2 и 3 - это тоже важнейшие нумерологические числа (первое чётное и первое нечётное числа; символы Земли и Неба и т.п.), однако их недостаточно. Для логики требуется пара 3 и 5 (или другая производная от этой пара).
Особый интерес (и вопрос) вызывают допустимые пары (3,6), (6,3), (6,12), (9,12), (12,6), (12,9) и, особенно, (3,9) и (9,3). Здесь явно не присутствует число 5, а в последних двух парах нет и числа 2. Правда, если записать 9=32, то число 2 появится. По-видимому, в этих случаях можно говорить о неявном присутствии 5 как пары 2 и 3, поскольку 2 и 3 обязательно присутствуют в каждой допустимой паре (2, может быть, как показатель степени числа 3) и, кроме того, 3 встречается ещё раз.
x y |
в этих графах десятичные числа | |
3 6 |
3 * 6 |
3 * (3*2) |
6 3 |
6 * 3 |
(3*2) * 3 |
6 C |
6 * 12 |
(3*2) * 3 * 22 |
C 6 |
12 * 6 |
22* 3 * (3*2) |
9 C |
9 * 12 |
3 * (3*2)2 |
C 9 |
12 * 9 |
(3*2)2* 3 |
3 9 |
3 * 9 |
3 * (3 2) |
9 3 |
9 * 3 |
(3 2) * 3 |
В заключение следует отметить, что каждая допустимая кодировка x и y, очевидно,
есть некоторая подстановка 
(4).
Поэтому каждой кодировке соответствует перестановочное преобразование (),
по которому она получается из основной кодировки x=3, y=5. В этом смысле перестановочное
преобразование можно интерпретировать как выбор другой кодировки.
В этом пункте мы дадим интерпретацию булевой алгебры через тетраграммы - сочетания
четырёх черт двух видов: целая черта ян ,
прерванная черта инь . Для этого
позициям тетраграммы поставим в соответствие двоичный разряд шестнадцатиричной
цифры: нижней позиции тетраграммы пусть соответствует 0-ой - младший - двоичный
разряд. Целую черту ян будем интерпретировать как "1", а прерванную
черту инь как "0".
В таком представлении логические операции, операндами которых являются тетраграммы, интерпретируются как теоретико-множественные операции: целая черта - это наличие элемента во множестве-тетраграмме, прерванная черта - отсутствие. Например:
5&C=4 интерпретируется как
&
=
Естественно, что и сами логические операции - через свои двоичные коды - интерпретируются как тетраграммы. Например:
& =
поскольку & = 3&5 = 1
&
=
Квадрат Дюрера в такой интерпретации выглядит так:
| F F |
2
x\y |
1
x&y |
C
x |
|
|
|
|
|
|
4
y\x |
9
x y |
A
y |
7
x y |
|
|
|
|
|
|
8
x y |
5
y |
6
x y |
B
y x |
|
|
|
|
|
|
3
x |
E
x y |
D
x y |
0
0 |
|
|
|
|
После этого встаёт вопрос об обратной интерпретации китайских триграмм (и гексаграмм), то есть сочетаний не 4-х, а 3-х (6-и) черт в терминах логических операций.
Число триграмм равно 8. Попробуем рассмотреть различные подмножества из восьми логических операций. Число всех таких подмножеств равно числу сочетаний из 16 по 8, то есть:
16! C168 = = 12.870. 8!8!
Мы будем рассматривать не все такие подмножества, а только те, которые в некотором смысле можно считать "естественными".
В п.5.1.5 мы изучали тождество структурных чисел (точнее, шестнадцатиричных цифр) и логических операций. Мы рассматривали операции вида p(a,b), где p,a,b - шестнадцатиричные цифры или, что тоже самое, логические операции. Таблицы операций вида p(a,b) приведены в Приложении 1.
Замкнутым подмножеством логических операций назовём такое множество U, которое
замкнуто относительно операций вида p(a,b), то есть 
p,a,bU
p(a,b)U. Очевидно,
множество всех логических операций, а также пустое множество, замкнуты. В Приложении
2 приведён полный список замкнутых подмножеств.
Нас будут интересовать замкнутые подмножества из восьми логических операций. Таких подмножеств девять (в Приложении 2 они выделены подчёркиванием):
| класс | N | замкнутые подмножества | число "1" | перестановка из подмножества, выделенного фоном | ||||||||
| числа | логические операции | 01234 | ||||||||||
| I | 52 | 01234567 | 0 | x&y | x\y | x | y\x | y | xy |
xy |
13310 | ------ |
| II | 118 | 13579BDF | x&y | x | y | xy |
xy |
yx |
xy |
F | 01331 | ------ |
| III | 102 | 03569ACF | 0 | x | y | xy |
xy |
y |
x |
F | 10601 | ------ |
| IV | 103 | 03478BCF | 0 | x | y\x | xy |
xy |
yx |
x |
F | 12221 | 3012 |
| 110 | 02578ADF | 0 | x\y | y | xy |
xy |
y |
xy |
F | 12221 | 3102 | |
| 117 | 02469BDF | 0 | x\y | y\x | xy |
xy |
yx |
xy |
F | 12221 | 1032 | |
| 120 | 016789EF | 0 | x&y | xy |
xy |
xy |
xy |
xy |
F | 12221 |  =3210 |
|
| 121 | 0145ABEF | 0 | x&y | y\x | y | y |
yx |
xy |
F | 12221 | 2013 | |
| 122 | 0123CDEF | 0 | x&y | x\y | x | x |
xy |
xy |
F | 12221 | 2103 | |
Предпоследняя графа таблицы указывает количество чисел из подмножества, которые имеют число "1" в своём двоичном коде, равное 0,1,2,3 или 4. Как видно, последние 6 подмножеств (класс IY) имеют одинаковый набор чисел. Последняя графа показывает перестановки разрядов, с помощью которых подмножества класса IY могут быть получены из подмножества, выделенного фоном (N 120 - 016789EF). Кстати, это подмножество состоит из всех восьми коммутативных логических операций. Таким образом, последние 6 подмножеств (класс IY) в некотором смысле эквивалентны: они могут быть получены друг из друга перестановкой двоичных разрядов числа. Напомним, что такая перестановка может интерпретироваться как выбор иного допустимого способа кодировки логических операций (п.5.4) или как перестановочное преобразование. Поэтому, фактически, мы имеем 4 класса таких подмножеств (I, II, III, IY).
Другой способ уменьшить число логических операций с 16 до 8 - наложить ограничения на операнды. В теоретико-множественной интерпретации булевой алгебры, как показано в п.3.7.1, два операнда x и y интерпретируются как два подмножества одного множества. В общем случае они разбивают всё множество на 4 базовые области:
x x\y x&y y\x
Именно поэтому получается 24=16 логических операций. Если потребовать, чтобы одна из базовых областей была пустой, то останется 3 базовые области, которым будут соответствовать 23=8 логических операций. Соответственно, мы имеем 4 варианта:
|
A: x 8=0 |
|
B: x&y=0 1=0 |
|
||||||||||||||||||||||||||||||||
|
C: x\y=0 2=0 |
|
D: y\x=0 4=0 |
|
||||||||||||||||||||||||||||||||
Каждой базовой области соответствует некоторая - базовая - логическая операция. Базовая операция - это операция, имеющая в своём двоичном коде только одну "1". В каждом из вариантов A,B,C,D соответствующая базовая логическая операция отождествляется с тождественной ложью (0). Соответственно, в каждом варианте логические операции отождествляются попарно: тождественными становятся те две логические операции, двоичные коды которых отличаются только в одном разряде - в том, в котором имеет "1" соответствующая базовая логическая операция, отождествляемая с 0.
| вариант | номер разряда | отождествление логических операций | |||||||
| A | 3 | 0=8 | 1=9 | 2=A | 3=B | 4=C | 5=D | 6=E | 7=F |
| B | 0 | 0=1 | 2=3 | 4=5 | 6=7 | 8=9 | A=B | C=D | E=F |
| C | 1 | 0=2 | 1=3 | 4=6 | 5=7 | 8=A | 9=B | C=E | D=F |
| D | 2 | 0=4 | 1=5 | 2=6 | 3=7 | 8=C | 9=D | A=E | B=F |
Таблица отождествления логических операций из предыдущего пункта даёт нам возможность определить, каким вариантам (A,B,C,D) соответствуют замкнутые подмножества из 8 логических операций:
| класс | N | замкнутые подмножества | варианты | |||||||||||
| числа | логические операции | A | B | C | D | |||||||||
| xy=0 |
x&y=0 | x\y=0 | y\x=0 | |||||||||||
| I | 52 | 01234567 | 0 | x&y | x\y | x | y\x | y | xy |
xy |
A | - | - | - |
| II | 118 | 13579BDF | x&y | x | y | xy |
xy |
yx |
xy |
F | - | B | - | - |
| III | 102 | 03569ACF | 0 | x | y | xy |
xy |
y |
x |
F | A | B | C | D |
| IV | 103 | 03478BCF | 0 | x | y\x | xy |
xy |
yx |
x |
F | - | B | C | - |
| 110 | 02578ADF | 0 | x\y | y | xy |
xy |
y |
xy |
F | - | B | - | D | |
| 117 | 02469BDF | 0 | x\y | y\x | xy |
xy |
yx |
xy |
F | A | B | - | - | |
| 120 | 016789EF | 0 | x&y | xy |
xy |
xy |
xy |
xy |
F | - | - | C | D | |
| 121 | 0145ABEF | 0 | x&y | y\x | y | y |
yx |
xy |
F | A | - | C | - | |
| 122 | 0123CDEF | 0 | x&y | x\y | x | x |
xy |
xy |
F | A | - | - | D | |
В логическом смысле основными являются варианты A,B,C,D, а выбор соответствующего замкнутого подмножества логических операций является "делом вкуса". Иными словами, при отождествлении двух логических операций выбор основной (попадающей в подмножество) и производной (тождественной основной) есть выбор той или иной нотации тождественных логических операций. Конечно, таких нотаций много (28=256), но мы рассматриваем только те, которые соответствуют замкнутым подмножествам логических операций, то есть подмножествам, "естественно" выделяемым и для общего случая (все базовые области непусты).
Теперь обратим внимание на классы замкнутых подмножеств. Классы I и II содержат
по одному подмножеству и однозначно соответствуют вариантам A (xy=0)
и B (x&y=0). Это случаи, когда множества x и y в совокупности покрывают
всё множество (A: xy=0)
или не имеют общих точек (B: x&y=0).
Каждое подмножество класса IY соответствует ровно двум вариантам и класс IY в целом соответствует всем возможным парам вариантов. Здесь можно считать главной пару вариантов (C,D) - случай, когда из двух множеств x и y одно является частью другого. Этой паре вариантов соответствует подмножество, выделенное фоном, - набор всех восьми коммутативных логических операций. Варианты C и D в известном смысле эквивалентны: выбор того или другого определяется тем, какое из двух множеств x и y вложено в другое.
Наибольший интерес представляет класс III, который мы рассмотрим отдельно в следующем пункте.
Класс III соответствует всем четырём вариантам A,B,C,D. Он состоит из одного подмножества логических операций 03569ACF, которое можно считать главным, поскольку при любом варианте, то есть при любом выборе одной из базовых областей как пустой, получающийся набор 8 логических операций можно интерпретировать как набор 03569ACF.
Как видно из Приложения 2, это главное подмножество - одно из семи замкнутых подмножеств, содержащих одновременно тождественную ложь = 0, тождественную истину = F и каждый из аргументов x = 3 и y = 5 (исходные высказывания в алгебре высказываний). В Приложении 2 эти 7 подмножеств выделены жирным шрифтом. Подмножество 03569ACF - единственное из них, содержащее 8 логических операций.
| N | числа | логические операции | число операций | |||||||||||||||
| 69 | 035F | 0 | x | y | F | 4 | ||||||||||||
| 71 | 0135F | 0 | x&y | x | y | F | 5 | |||||||||||
| 85 | 0357F | 0 | x | y | xy |
F | 5 | |||||||||||
| 87 | 01357F | 0 | x&y | x | y | xy |
F | 6 | ||||||||||
| 101 | 035ACF | 0 | x | y | y |
x |
F | 6 | ||||||||||
| 102 | 03569ACF | 0 | x | y | xy |
xy |
y |
x |
F | 8 | ||||||||
| 123 | 0123456789ABCDEF | 0 | x&y | x\y | x | y\x | y | xy |
xy |
xy |
xy |
y |
yx |
x | xy |
xy |
F | 16 |
Подмножество 03569ACF содержит все нуль-арные и унарные операции (0F и 35AC)
плюс две коммутативные и ассоциативные операции: исключающая дизъюнкция = 6
и эквивалентность = 9, которые являются отрицанием друг друга. Вообще, подмножество
03569ACF вместе с каждой логической операцией содержит и её отрицание (что,
впрочем, следует из замкнутости подмножества и наличия в нём операций отрицания
x и y):
0=F, 3=C,
5=A, 6=9.
Подмножество 03569ACF состоит из всех чисел (шестнадцатиричных цифр), двоичный код которых содержит чётное число "1": 0 - 0, 2 - 3569AC, 4 -F. Поэтому оно инвариантно к любому перестановочному преобразованию. Подмножество 03569ACF - одно из 6 замкнутых подмножеств (в Приложении 2 выделены курсивом), которые обладают этим свойством инвариантности.
| N | числа | логические операции | число операций | |||||||||||||||
| 1 | 0 | |||||||||||||||||
| 2 | 0 | 0 | 1 | |||||||||||||||
| 56 | F | F | 1 | |||||||||||||||
| 57 | 0F | 0 | F | 2 | ||||||||||||||
| 102 | 03569ACF | 0 | x | y | xy |
xy |
y |
x |
F | 8 | ||||||||
| 123 | 0123456789ABCDEF | 0 | x&y | x\y | x | y\x | y | xy |
xy |
xy |
xy |
y |
yx |
x | xy |
xy |
F | 16 |
Триграммы можно интерпретировать как частный случай тетраграмм, а именно - как тетраграммы, верхняя позиция которых занята прерванной чертой инь. В китайской нумерологии "ЛОЖЬ" и "ИСТИНУ" скорее следовало бы интерпретировать как "ИНЬ" и "ЯН". Тогда числа, соответствующие триграммам, - это первые 8 шестнадцатиричных цифр, то есть 8 восьмеричных цифр (01234567). В квадратно-круговом расположении триграмм это будет выглядеть так:
Расположение Фу Си Расположение Вэнь-вана
3 7 6 5 2 1 0 4
6 5 0 1 3 4 2 7
x x x y x\y x&y ИНЬ y\x
x y ИНЬ x&y x y\x x\y x
Здесь, очевидно, мы имеем замкнутое подмножество логических операций 01234567,
составляющее класс I и соответствующее варианту A (xy=0),
когда x и y в совокупности покрывают всё множество (все три позиции триграммы),
то есть xy=F
(ЯН).
Можно отметить, что при других допустимых кодировках, которые определяются тем, каким двоичным разрядам числа соответствуют три позиции триграммы, будут получаться несколько иные расположения логических операций. Например, при кодировке x=3, y=6 имеем:
Расположение Фу Си Расположение Вэнь-вана
x x y x x&y x\y ИНЬ y\x
y x ИНЬ x\y x y\x x&y x
Для главного подмножества логических операций 03569ACF при обычной кодировке x=3, y=5, используя теоретико-множественную интерпретацию логических операций, имеем:
0 = ИНЬ
3 = x
5 = y
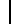
6 = x 9 = x A = C = F = ЯН
Расположение Фу Си Расположение Вэнь-вана
x ЯН x y x ИНЬ
x y ИНЬ x x ЯН
При других кодировках будут получаться другие расположения логических операций. Например, при x=3, y=6 имеем:
Расположение Фу Си Расположение Вэнь-вана
x ЯН y x x ИНЬ
y x ИНЬ x x ЯН
Во всех вариантах расположения по Фу Си мы видим, что центрально-симметричные клетки девятиклеточного квадрата заняты логическими операциями, являющимися отрицаниями друг друга.
Можно расположить логические операции и в кресте Хэ Ту, есливоспользоваться стандартной схемой преобразования квадрата Ло Шу в крест Хэ Ту:
квадрат ЛО ШУ
4 9
2
73
85 1
крест ХЭ ТУ
7 2 8 3
5 10 4 9 1 6
Например, для подмножества 03569ACF при кодировке x=3, y=5 имеем:
Расположение Фу Си
x x y
x ЯН ИНЬ
Расположение Вэнь-вана
x ИНЬ x
x y ЯН
Мы видим, что "инь" занимает в кресте Хэ Ту одну из четырёх внутренних позиций, а "ян" - одну их четырёх внешних позиций. Это коррелирует с представлением об "инь" как о внутреннем, скрытом, тайном и об "ян" как о внешнем, открытом, явном.
В расположении Фу Си "инь" и "ян" находятся друг против друга (центрально-симметричны) в квадрате Ло Шу, а в расположении Вэнь-вана - наоборот, в кресте Хэ Ту.
В кресте Хэ Ту по Фу Си 4 внутренние позиции заняты "внутренними"
логическими операциями ИНЬ, x, y, xy,
то есть операциями в теоретико-множественном смысле не выводящими за пределы
объединения x и y. Соответственно, 4 внешние позиции заняты "внешними"
логическими операциями ЯН, x,
y, xy,
каждая из которых в теоретико-множественном смысле выводит за эти пределы до
границ "внешнего мира". Действительно:
0\(x F\(x x\(x ( y\(x ( (x (x
"Внешний мир" вырождается до пустого множества только в варианте
A, когда xy=0.
Любое подмножество B логических операций естественно
расширяется до замкнутого множества Z применением
операций вида p(a,b) (Приложение 1). Будем говорить,
что B - порождающее множество для множества Z,
и Z - замыкание множества B,
и обозначать Z={B}.
Среди порождающих множеств можно выделить минимальные порождающие множества:
множество B - минимально, если любое его истинное
подмножество имеет другое замыкание, то есть А
B
{А}{B}(очевидно,
{А}{B}).
В Приложении 3 приведён список список всех минимальных
порождающих множеств логических операций и их замыканий. В частности, все минимальные
множества, порождающие всё множество логических операций. Видно, например, что
все логические операции могут быть получены из тройки 3,5,8 (x,y,xy)
или из тройки 3,5,E (x,y,xy),
то есть с использованием (кроме x и y) только одной операции "стрелка Пирса"
или "Штрих Шеффера".
Рассмотрим список минимальных множеств, порождающих главное подмножество 03569ACF.
{0 3 9 }= 0 3 56 9A C F
{0 5 9 }= 0 3 56 9A C F
{ 3 6 9 }= 0 3 56 9A C F
{ 56 9 }= 0 3 56 9A C F
{ 6 A }= 0 3 56 9A C F
{ 9A }= 0 3 56 9A C F
{ 6 C }= 0 3 56 9A C F
{ 9 C }= 0 3 56 9A C F
{ 3 6 F}= 0 3 56 9A C F
{ 56 F}= 0 3 56 9A C F
Особый интерес представляют минимальные множества, состоящие только из двух операций:
числа операции триграммы названия триграмм 6 A
x
ДЕРЕВО ВОДА 9 A
x
ГРОМ ВОДА 6 C
x
ДЕРЕВО ГОРА 9 C
x
ГРОМ ГОРА
|
|
|
|
